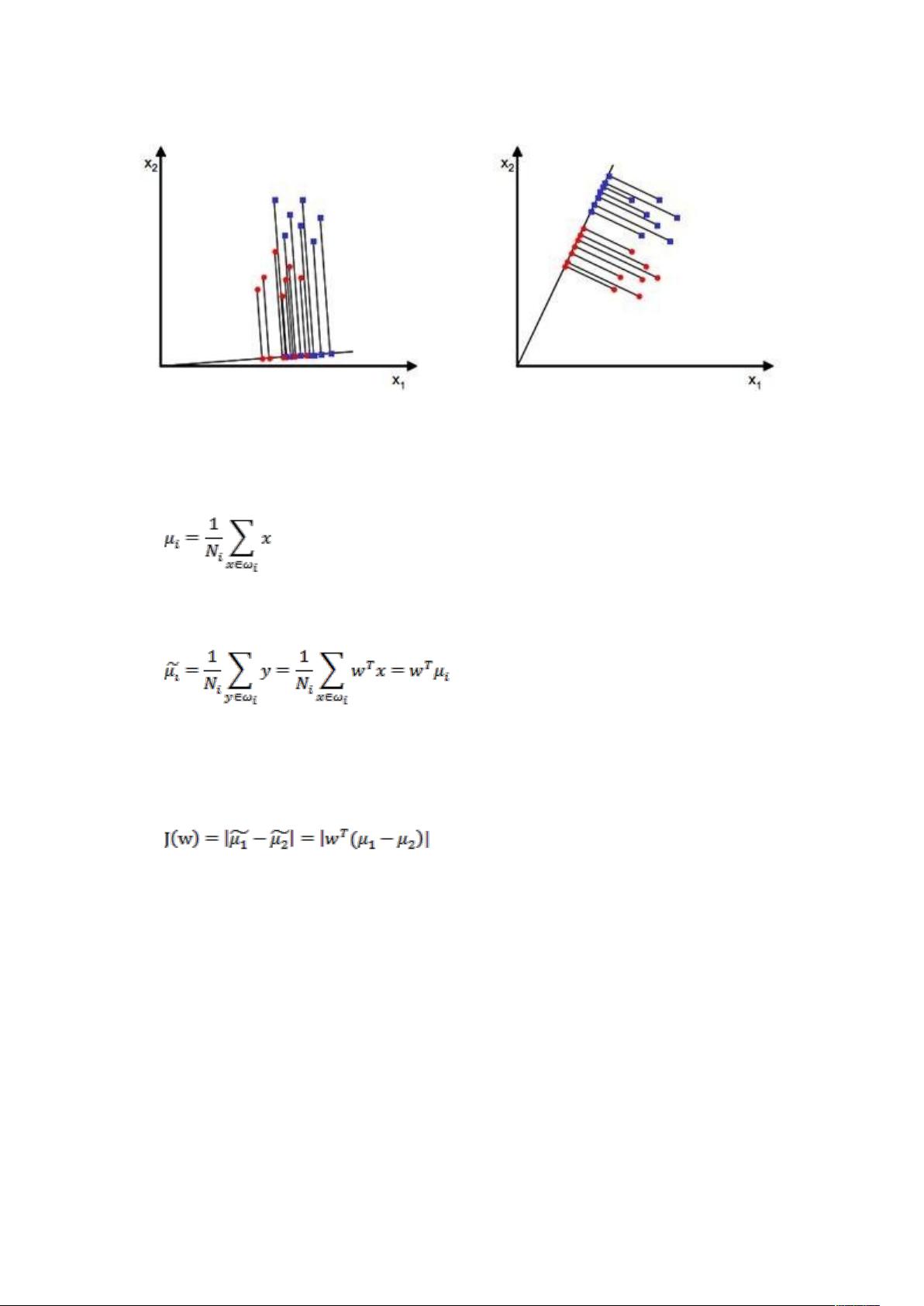
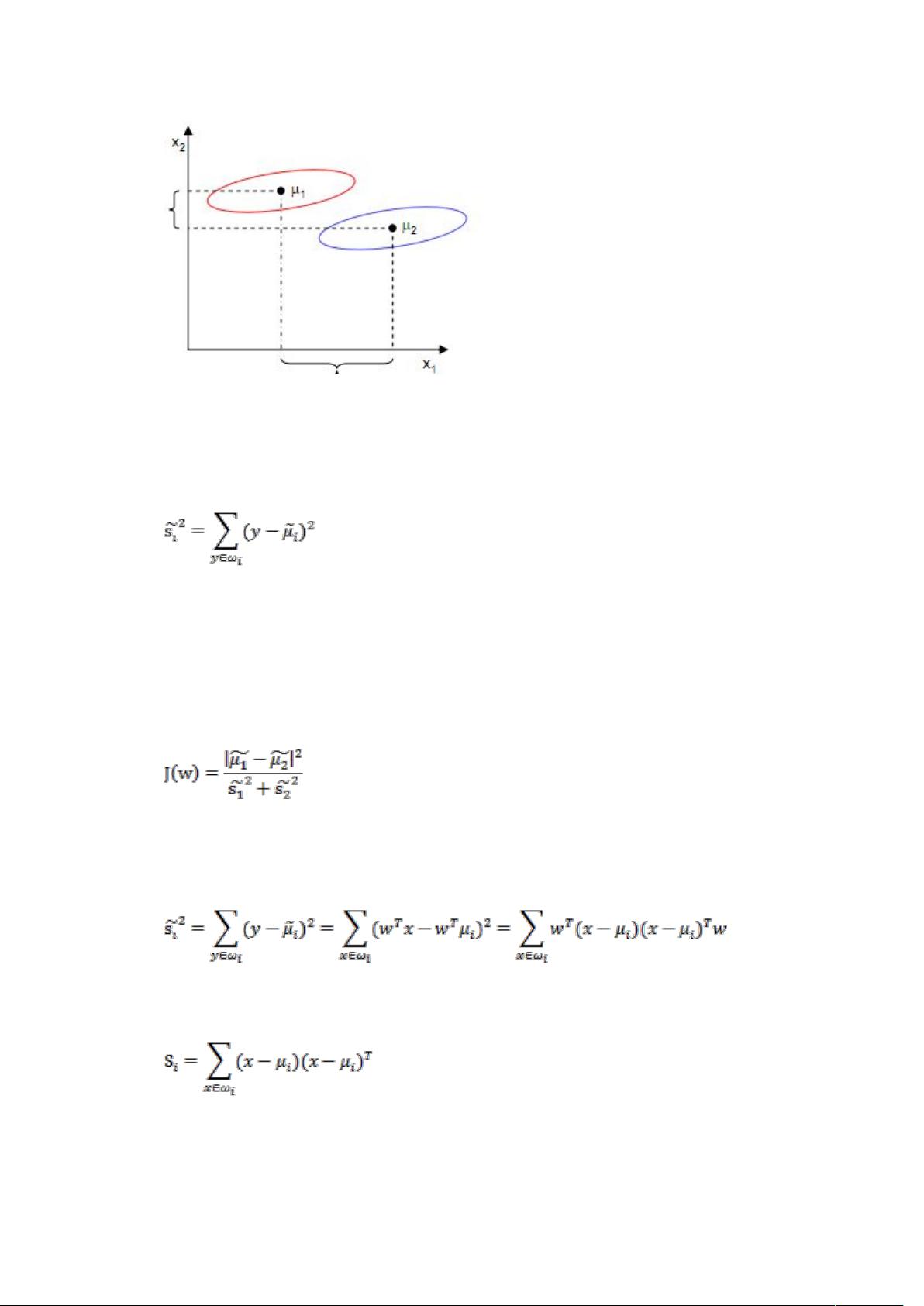
线性判别分析(LDA)

线性判别分析(LDA) 线性判别分析（Linear Discriminant Analysis，简称 LDA）是一种常用的降维技术，主要用于处理高维数据的分类问题。LDA 的主要思想是寻找一个线性投影，使得投影后的数据点能够被清晰地分离出来。 在介绍 LDA 之前，先回顾一下之前讨论的 PCA 和 ICA。PCA 是一种无监督的降维方法，它可以将高维数据降低到低维空间，但它没有考虑类别标签 y。ICA 也是一种无监督的降维方法，它可以将信号分离成独立的成分，但也没有考虑类别标签 y。 现在，假设我们有一个分类问题，需要将一张 100*100 像素的图片识别出人脸，我们可以使用 LDA 将其降维到低维空间，然后进行分类。 LDA 的主要思想是寻找一个线性投影，使得投影后的数据点能够被清晰地分离出来。我们可以定义一个函数 J(w)，它表示投影后的类别中心点之间的距离。则我们的目标是寻找一个最佳的投影向量 w，使得 J(w) 最大。 我们可以找到每类样本的均值（中心点），然后计算投影后的样本均值。接着，我们可以定义一个散列值（scatter），它表示投影后的类求散列值。我们的目标是寻找一个最佳的投影向量 w，使得 J(w) 最大，同时使得散列值最小。 使用 LDA，可以将高维数据降低到低维空间，并且能够保留类别信息。LDA 广泛应用于图像识别、文本分类、生物信息学等领域。 下面是一个简单的 LDA 实现： 我们需要计算每类样本的均值（中心点）： $$\mu_i = \frac{1}{N_i} \sum_{x \in X_i} x$$ 其中，$X_i$ 是第 i 类样本，$N_i$ 是第 i 类样本的数量。 然后，我们可以计算投影后的样本均值： $$\hat{\mu_i} = \frac{1}{N_i} \sum_{x \in X_i} w^T x$$ 接着，我们可以定义一个散列值（scatter）： $$S = \frac{1}{N} \sum_{x \in X} (w^T x - \hat{\mu}) (w^T x - \hat{\mu})^T$$ 我们的目标是寻找一个最佳的投影向量 w，使得 J(w) 最大，同时使得散列值最小。 使用拉格朗日乘子，我们可以将这个问题转换为一个最优化问题： $$\max_{w} J(w) = \max_{w} \frac{w^T S_B w}{w^T S_W w}$$ 其中，$S_B$ 是 between-class scatter matrix，$S_W$ 是 within-class scatter matrix。 求解这个最优化问题，我们可以得到一个闭式解： $$w = S_W^{-1} S_B$$ 这就是 LDA 的基本思想和实现过程。LDA 广泛应用于机器学习和数据挖掘领域，是一种非常有用的降维技术。