GMM估计方法.pdf

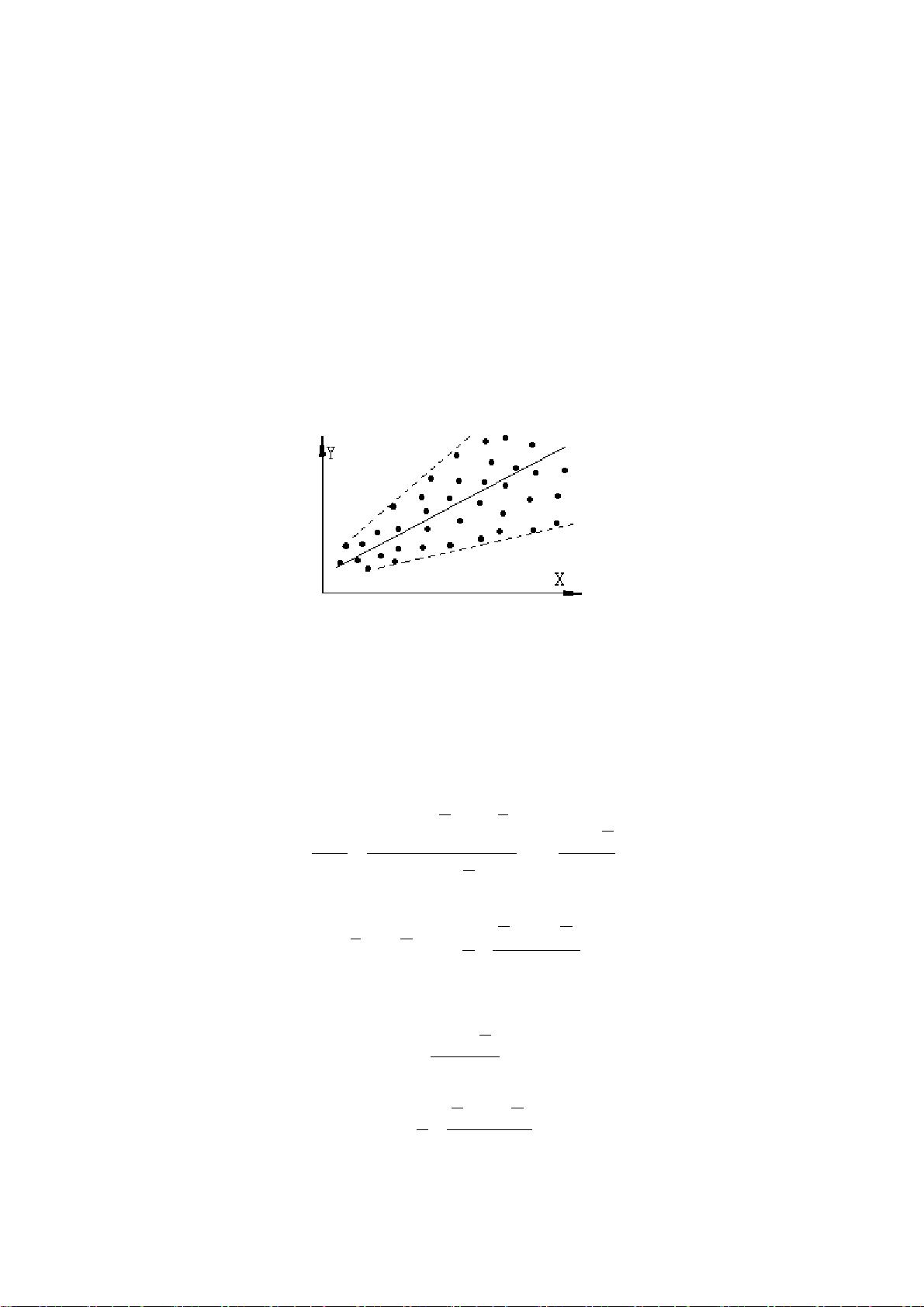
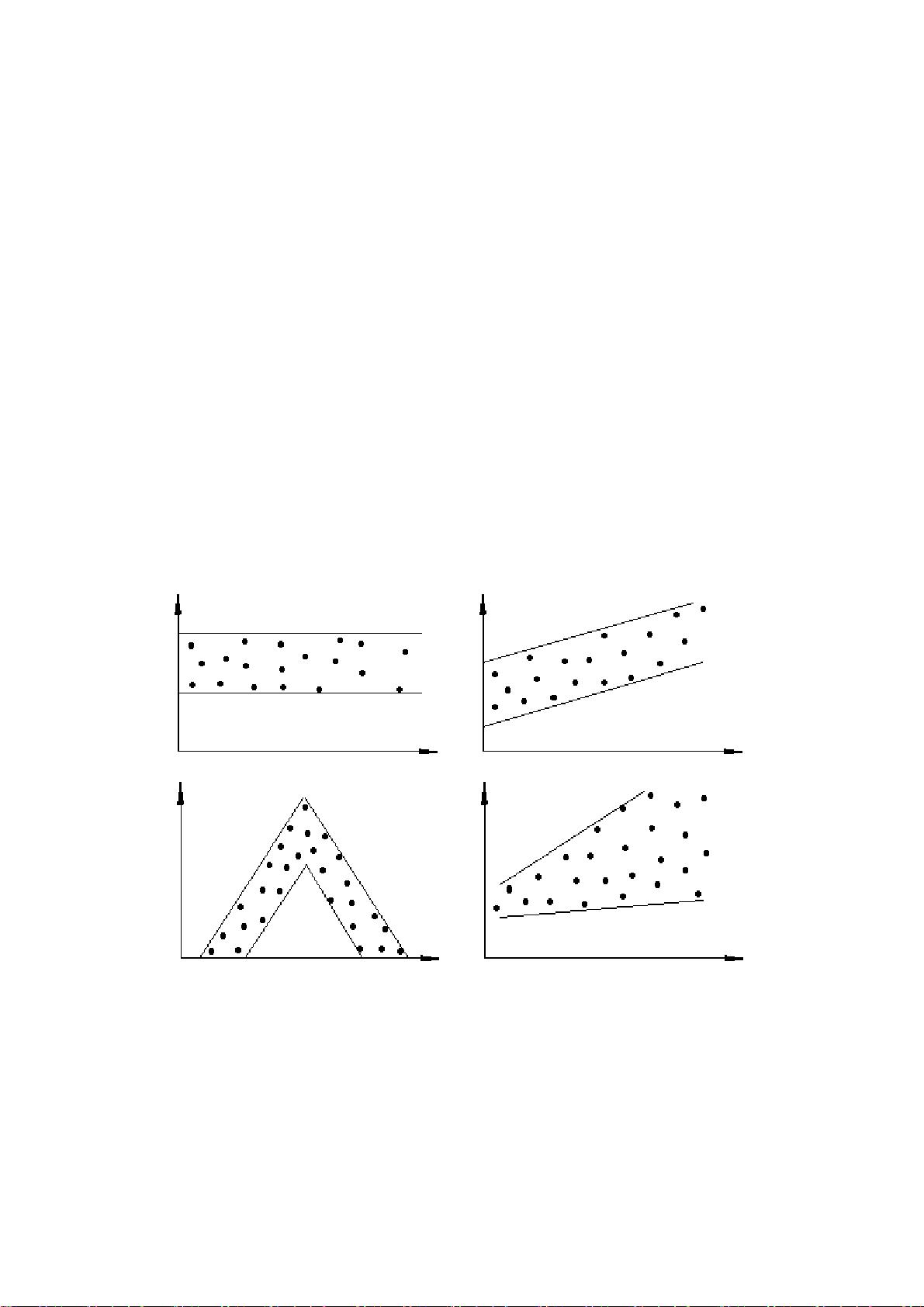
GMM 估计方法 GMM 估计方法是指广义矩估计方法，它是一种常用的参数估计方法，广泛应用于经济学、金融学、管理科学等领域。GMM 估计方法的基本思想是对观测数据进行变换，使之重新具有相同的方差，然后对变换后的数据进行最小二乘估计。 在第四章中，我们讨论了异方差与自相关广义线性模型。在前三章中，我们讨论了线性模型的假设条件，即残差的方差相同。但是，在实际应用中，这个假设条件并不总是成立。因此，我们需要对线性模型进行改进，使其能够适应异方差的情况。 改进的基本思路是对观测数据进行适当的变换，使之重新具有相同的方差。我们可以通过引入变换矩阵 P，使得 Φ=′PP，其中 Φ 是残差的协方差矩阵。然后，我们可以对变换后的数据进行最小二乘估计，从而得到广义最小二乘解。 在第四章中，我们还讨论了异方差的存在与检验、自相关广义线性模型、残差一阶自回归线性模型、自回归条件异方差模型、广义矩估计方法等内容。 在异方差的存在与检验中，我们讨论了异方差的定义和检验方法。我们可以通过检验残差的方差是否相同来检测异方差的存在。 在自相关广义线性模型中，我们讨论了残差的自相关性和异方差性。我们可以通过引入自相关项来改进线性模型，使其能够适应自相关和异方差的情况。 在残差一阶自回归线性模型中，我们讨论了残差的一阶自回归性和异方差性。我们可以通过引入残差的一阶自回归项来改进线性模型，使其能够适应残差的一阶自回归性和异方差性。 在自回归条件异方差模型中，我们讨论了残差的自回归性和异方差性。我们可以通过引入自回归项和异方差项来改进线性模型，使其能够适应残差的自回归性和异方差性。 在广义矩估计方法中，我们讨论了广义矩估计的基本思想和应用。我们可以通过对观测数据进行变换，使之重新具有相同的方差，然后对变换后的数据进行最小二乘估计，从而得到广义最小二乘解。 第四章讨论了异方差和自相关广义线性模型的改进方法，包括对观测数据的变换、残差的一阶自回归性和异方差性、自回归条件异方差模型和广义矩估计方法等内容。这章的内容对经济学、金融学、管理科学等领域的研究和应用具有重要的参考价值。