
GRAPH DRAWING BY FORCE-DIRECTED PLACEMENT
1131
needs to recalculate the contribution of that vertex to the energy of the system,
taking
Θ
(|
V
|) time.
Davidson and Harel1
10
also lay out graphs by reducing the energy of a system, but
use a method having older roots in VLSI placement and other optimization problems:
simulated annealing.
11,12
Simulated annealing is a powerful, general, optimization
technique, but it is computationally costly. The problem of drawing a graph is
restated as a problem in minimizing energy and therefore one of optimization.
Applying simulated annealing requires choosing an energy function—Davidson and
Hare] picked a flexible function combining terms for vertex distribution, nearness
to borders, edge-lengths, and edge-crossings. The weights on these terms can be
varied to emphasize different aesthetic standards.
Davidson and Harel tried to be flexible in meeting different aesthetic standards
and in producing the highest quality figures; they have a ‘fine-tuning’ option that,
after the basic configuration is found using simulated annealing, makes adjustments
a few pixels at a time, forbidding ‘up-hill’ moves. We will pick up the threads of
this idea later in this paper. Despite using updates of only
Θ (| V |) time complexity
in its inner loop, simulated annealing is extremely slow and impractical for interactive
display of graphs.
A NEW METHOD
We have only two principles for graph drawing:
1. Vertices connected by an edge should be drawn near each other.
2. Vertices should not be drawn too close to each other.
How close vertices should be placed depends on how many there are and how much
space is available. Some graphs are too complicated to draw attractively at all. Our
vague guidelines recall a result from particle physics:
5
At a distance of about 1 fm [femto-meter] the strong nuclear force is
attractive and about 10 times the electric force between two protons. The
force decreases rapidly with increasing distance, becoming completely
negligible at about 15 times this separation. When two nucleons are within
about 0·4 fm of each other, the strong nuclear forces become repulsive.
Thus nuclei do not collapse.
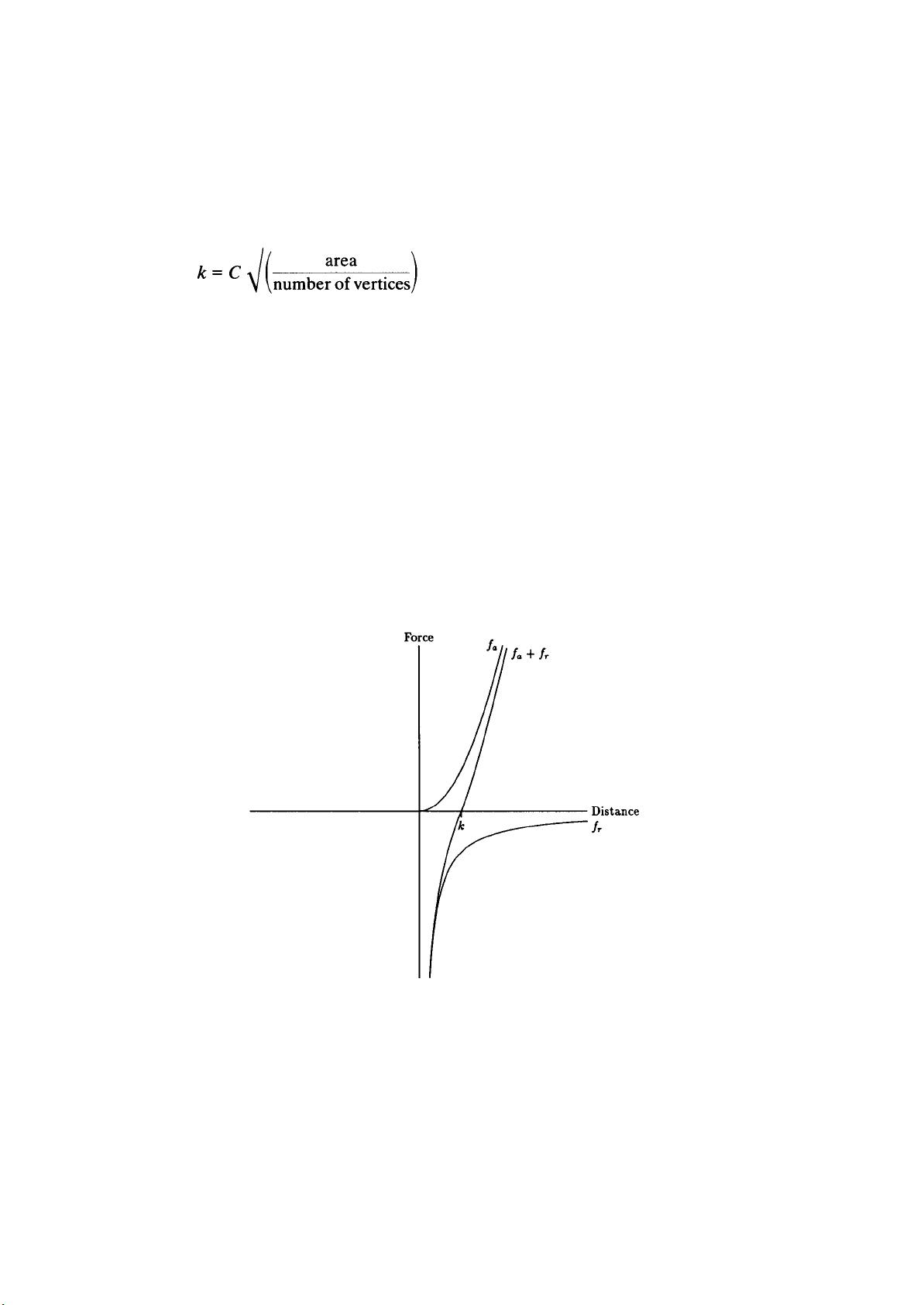
Consider the following analogy: the vertices behave as atomic particles or celestial
bodies, exerting attractive and repulsive forces on one another; the forces induce
movement. Our algorithm will resemble molecular or planetary simulations, some-
times called n -body problems. Following Eades, however, we know that we need
not have a faithful simulation; we can apply unrealistic forces in an unrealistic
manner. So, like Eades, we make only vertices that are neighbours attract each
other, but all vertices repel each other. This is consistent with the asymmetry of our
two guidelines above.
We were inspired by natural systems such as springs and macro-cosmic gravity,
but must point out that the ‘forces’ are not correctly named. We use forces to
calculate velocity for every time quantum (and thus displacement, since the time of
a quantum is unity), whereas true forces induce acceleration. The distinction is

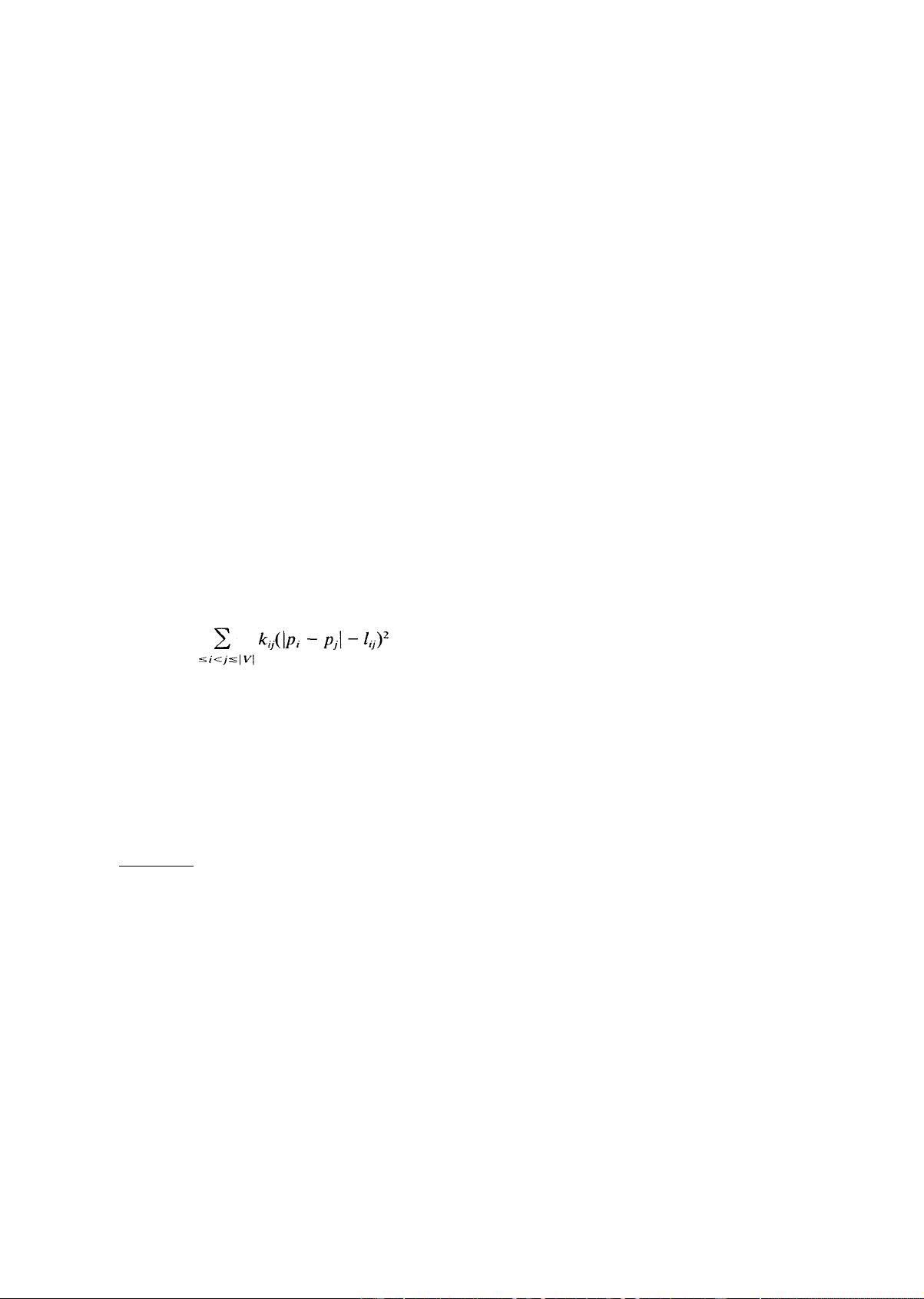


 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功
- 1
- 2
前往页