An Idiot’s guide to Support vector machines (SVMs)

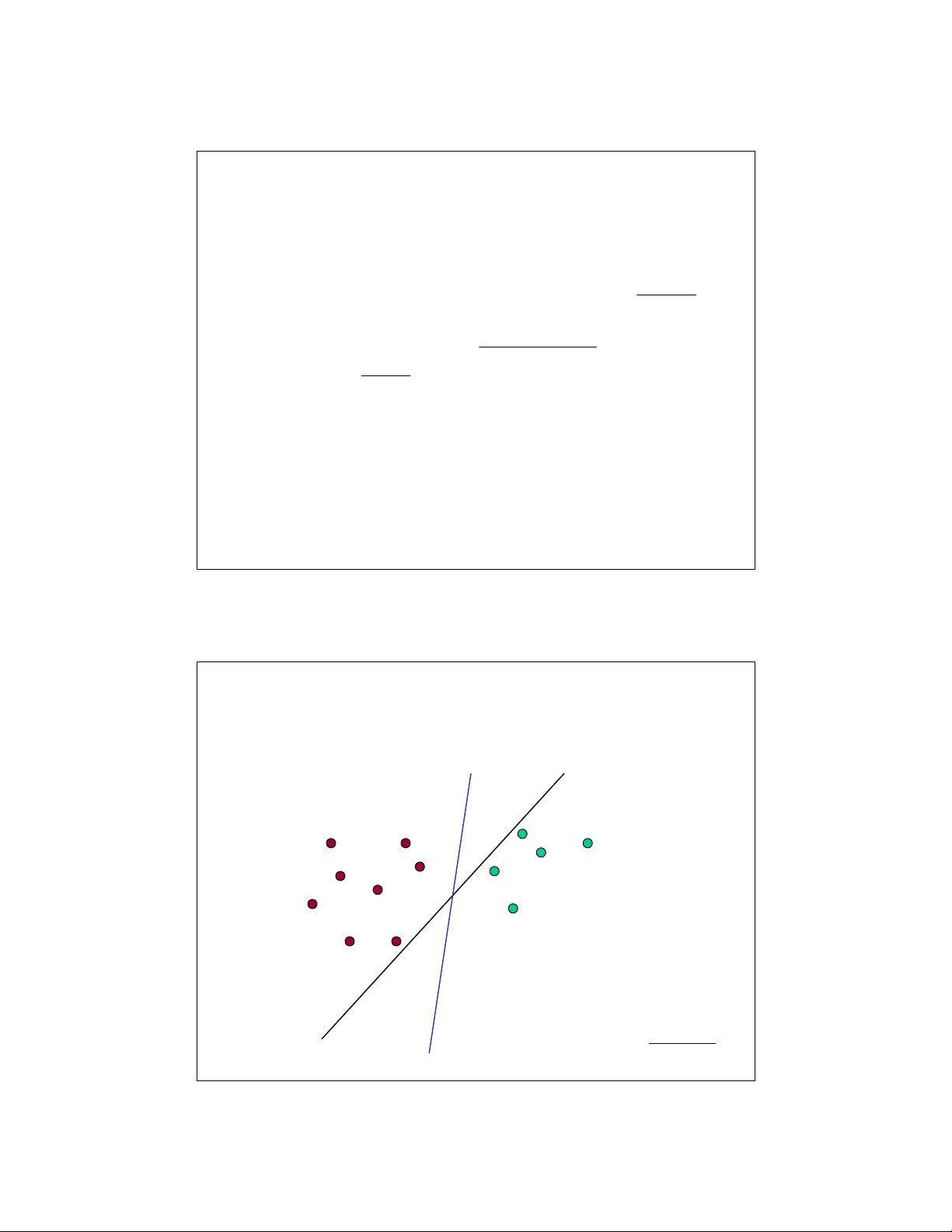
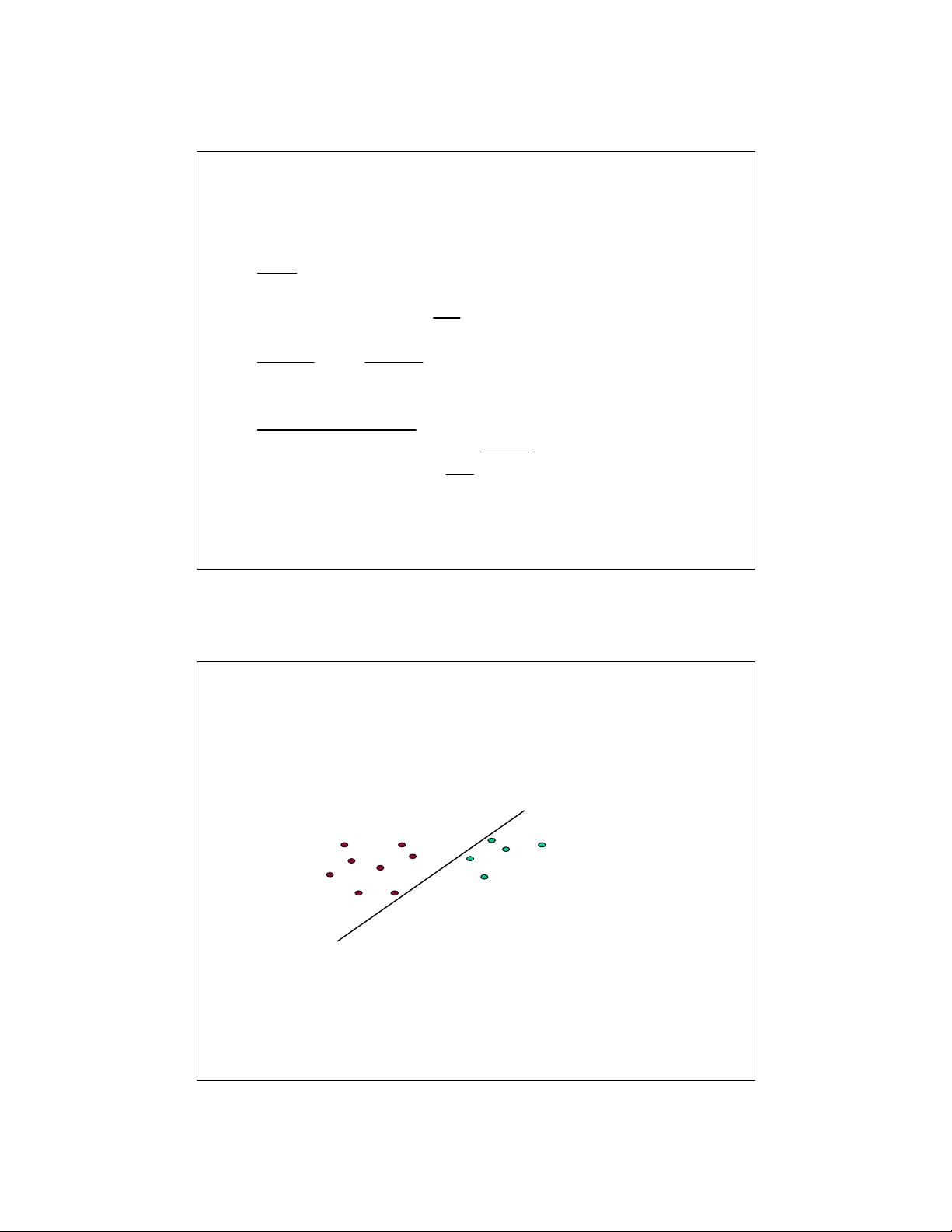
《支持向量机傻瓜指南》主要介绍了一种广泛应用于机器学习领域的算法——支持向量机（Support Vector Machine，SVM）。该算法属于学习算法的新一代，在处理线性可分模式和非线性模式方面具有独特的理论优势和高效率的学习方法。下面详细说明文章中提到的关键知识点。 文章提到了SVM的发展背景和主要思想。在1980年代之前，几乎所有的学习方法都学习线性决策面，线性学习方法具有良好的理论性质，但仅限于线性问题。到了1980年代，决策树和神经网络（NNs）允许有效学习非线性决策面，但它们缺乏理论基础，并且在实际应用中容易陷入局部最小值。到了1990年代，基于计算学习理论发展出了一种新的非线性函数的高效学习算法，具有很好的理论性质。 文章指出，在过去十年内有两个独立的进展促进了SVM的发展。首先是通过“核函数”实现了非线性区域的新高效可分性，这将相似度的概念推广到了基于点积的新类型相似度度量。其次是使用二次优化问题避免了神经网络的局部最小问题。最终产生的学习算法是一个优化算法，而非贪心搜索。 SVM的基本思想与单层或多层神经网络相似，它为线性可分模式寻找最优超平面。对于非线性可分的模式，则通过转换原始数据到一个新空间来扩展，这里的核函数起到了关键作用。SVM算法在模式识别中的主要目的是最大化分类间隔（Winston术语称为“街道”），这个间隔是由支持向量所定义的。支持向量是最靠近决策表面（或超平面）的数据点，它们是最难分类的数据点，对决策表面的最优位置有直接影响。最优超平面是由具有最低容量（独立特征/参数数量）的函数类得出的。 在SVM的发展历程中，作者提到了决策超平面的选择问题。一般而言，存在许多可能的解决方案，SVM可以找到一个最优解。支持向量机（SVM）最大化了分类间隔，决策函数是由训练样本的一小部分子集（通常是支持向量）完全指定的。这最终归结为一个二次规划问题，可以通过标准方法轻松解决。 SVM是一种基于统计学习理论的强大的监督学习方法，尤其擅长于在数据维度大于样本数量的情况下处理模式识别问题，如文本分类、生物信息学、生物特征识别等。SVM的核心是寻找数据的最佳边界，这个边界可以最大化各类数据之间的间隔，因此具备良好的泛化能力。SVM的核技巧允许它处理那些线性不可分的数据，通过将数据映射到更高维的空间中，使用适当的核函数来处理非线性特征，使得原本在低维空间线性不可分的数据在高维空间中可以线性分割。 该算法在学习过程中非常注重少数支持向量的作用，这些支持向量是决定了最终决策边界的点。而且，SVM的训练过程中所涉及的优化问题具有全局最优解的保证，这使得SVM在很多应用中成为首选的算法之一。此外，SVM在处理大规模数据集时，由于其解的稀疏性（只有一小部分数据点被用作支持向量），在实际应用中具有一定的优势。