【课件】5.3.1_1二叉树的先中后序遍历.pdf

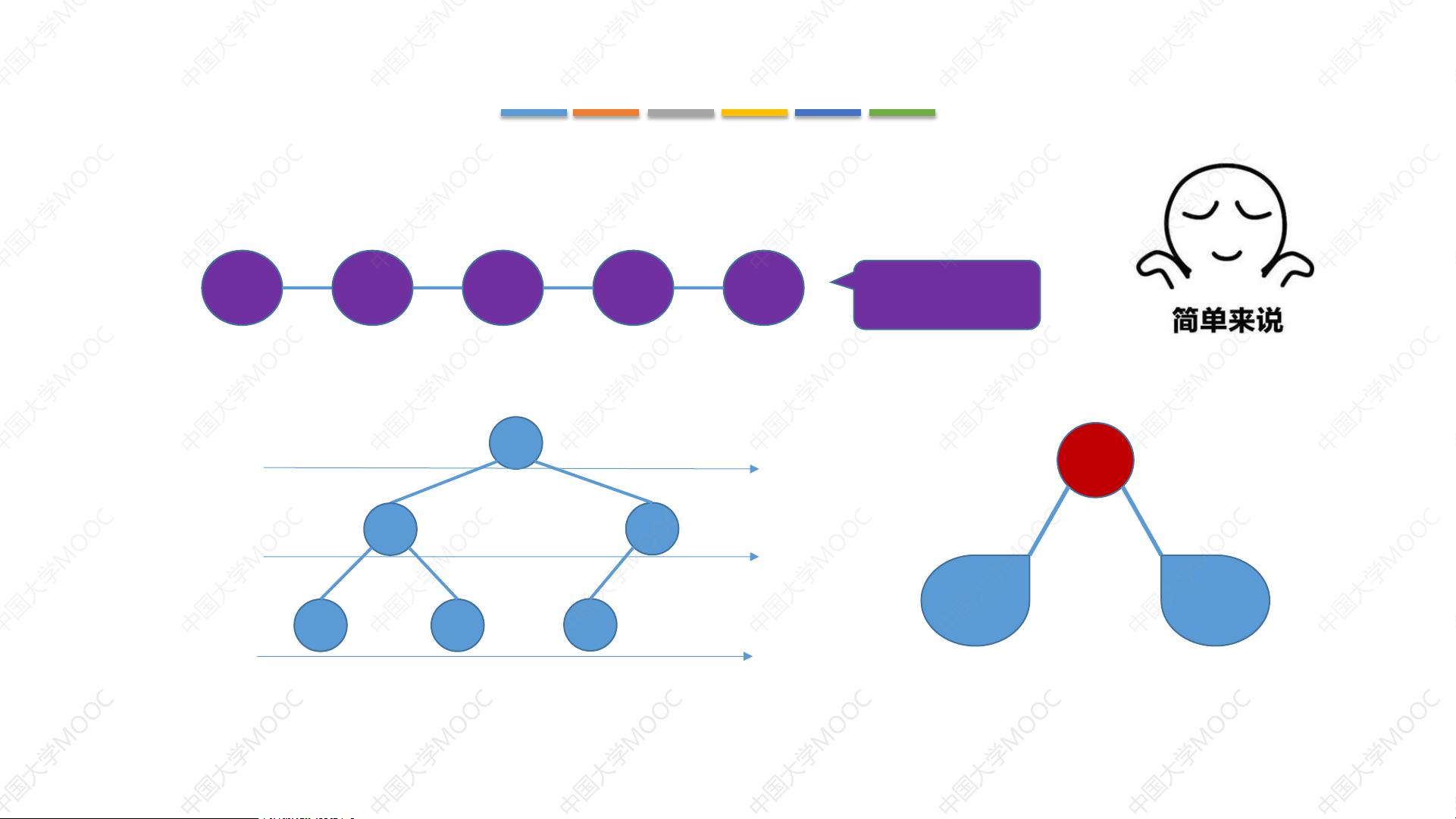
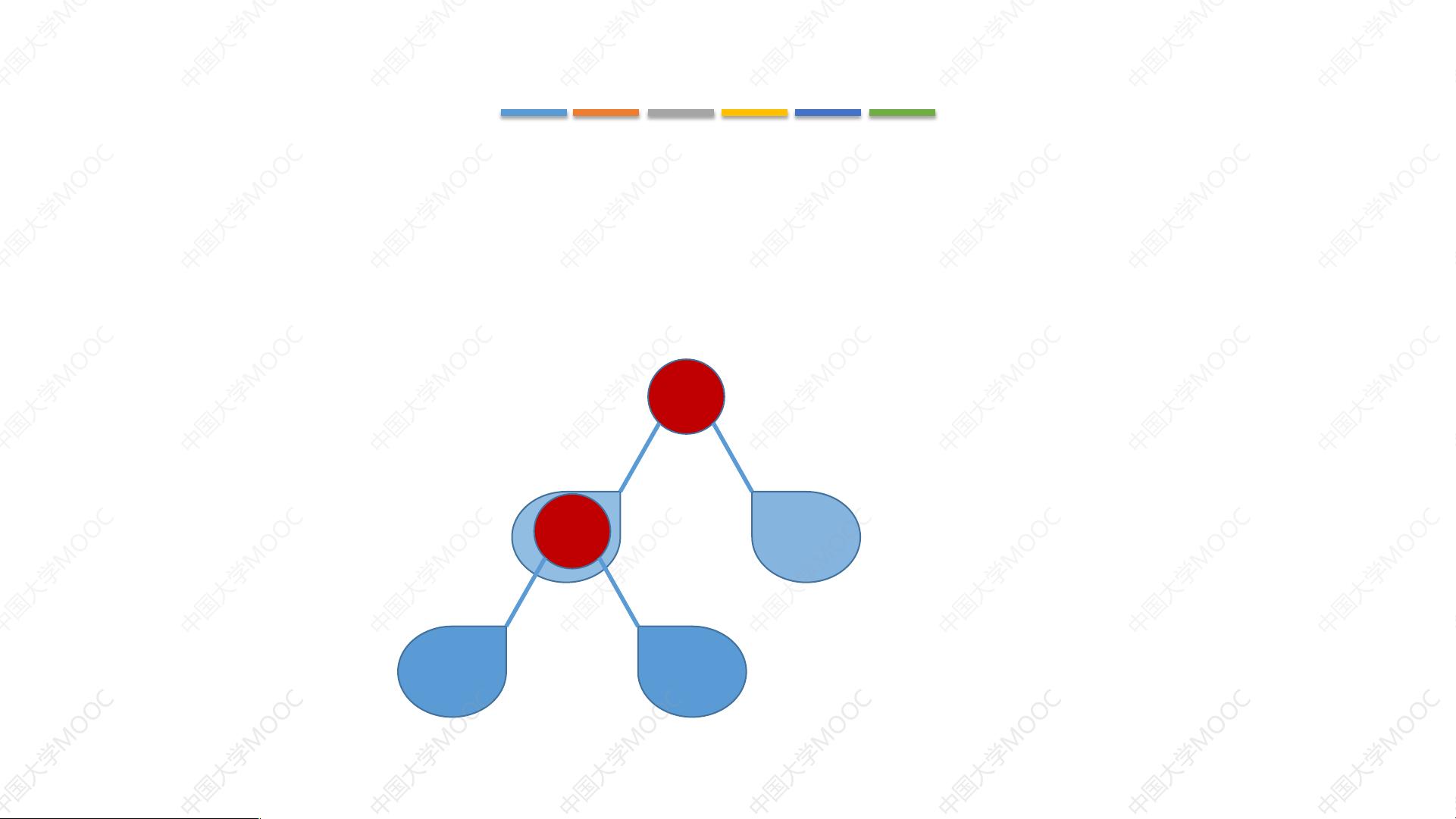
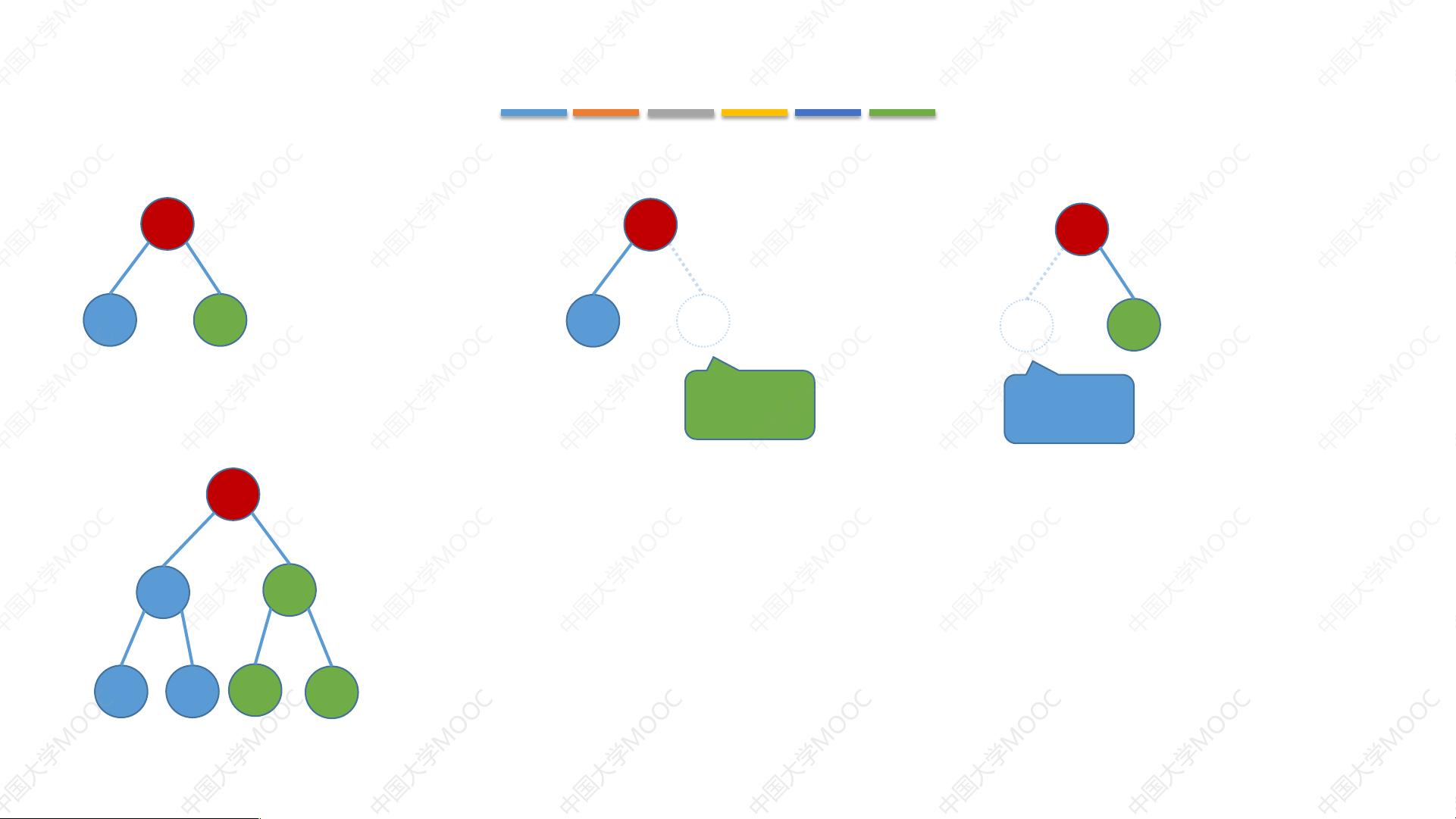
根据给定文件的信息，我们可以明确地了解到文档的主题是关于二叉树的三种遍历方法：先序遍历、中序遍历以及后序遍历。接下来，我们将详细地阐述这三种遍历方式的概念、实现原理及其应用场景。 ### 一、先序遍历 #### 1.1 定义 先序遍历是指按照“根节点->左子树->右子树”的顺序进行遍历的一种方式。具体步骤为： - 首先访问根节点； - 然后递归地遍历左子树； - 最后递归地遍历右子树。 #### 1.2 实现方法 先序遍历可以通过递归的方式实现： ```java public void preorderTraversal(TreeNode root) { if (root == null) return; // 访问当前节点 System.out.print(root.val + " "); // 递归遍历左子树 preorderTraversal(root.left); // 递归遍历右子树 preorderTraversal(root.right); } ``` 除了递归方法之外，也可以使用栈来实现非递归版本的先序遍历： ```java public void nonRecursivePreorderTraversal(TreeNode root) { if (root == null) return; Stack<TreeNode> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode node = stack.pop(); System.out.print(node.val + " "); if (node.right != null) { stack.push(node.right); } if (node.left != null) { stack.push(node.left); } } } ``` ### 二、中序遍历 #### 2.1 定义 中序遍历的顺序是“左子树->根节点->右子树”。具体步骤为： - 递归遍历左子树； - 访问根节点； - 递归遍历右子树。 #### 2.2 实现方法 中序遍历同样可以采用递归的方式实现： ```java public void inorderTraversal(TreeNode root) { if (root == null) return; // 递归遍历左子树 inorderTraversal(root.left); // 访问当前节点 System.out.print(root.val + " "); // 递归遍历右子树 inorderTraversal(root.right); } ``` 非递归版本的中序遍历则可以利用栈来完成： ```java public void nonRecursiveInorderTraversal(TreeNode root) { if (root == null) return; Stack<TreeNode> stack = new Stack<>(); TreeNode curr = root; while (curr != null || !stack.isEmpty()) { while (curr != null) { stack.push(curr); curr = curr.left; } curr = stack.pop(); System.out.print(curr.val + " "); curr = curr.right; } } ``` ### 三、后序遍历 #### 3.1 定义 后序遍历遵循“左子树->右子树->根节点”的顺序。具体步骤为： - 递归遍历左子树； - 递归遍历右子树； - 访问根节点。 #### 3.2 实现方法 后序遍历同样支持递归和非递归两种实现方式： ```java public void postorderTraversal(TreeNode root) { if (root == null) return; // 递归遍历左子树 postorderTraversal(root.left); // 递归遍历右子树 postorderTraversal(root.right); // 访问当前节点 System.out.print(root.val + " "); } ``` 对于非递归版本，后序遍历较为复杂，通常需要额外的数据结构来辅助实现： ```java public void nonRecursivePostorderTraversal(TreeNode root) { if (root == null) return; Stack<TreeNode> stack = new Stack<>(); TreeNode curr = root; TreeNode lastVisited = null; // 上一个访问过的节点 while (curr != null || !stack.isEmpty()) { while (curr != null) { stack.push(curr); curr = curr.left; } curr = stack.peek(); // 当前考虑访问的节点 if (curr.right == null || curr.right == lastVisited) { // 如果没有右子树或已经访问过右子树 System.out.print(curr.val + " "); lastVisited = curr; stack.pop(); } else { // 否则继续访问右子树 curr = curr.right; } } } ``` ### 四、应用场景 二叉树的这三种遍历方式在实际应用中有不同的用途： - **先序遍历**：常用于复制一棵二叉树。 - **中序遍历**：对于二叉搜索树而言，中序遍历可以得到从小到大的排序序列。 - **后序遍历**：常用于表达式树，例如后缀表达式的计算等。 以上就是对二叉树的先序、中序和后序遍历方法的详细介绍。希望这些内容能够帮助读者更好地理解和掌握这些重要的数据结构操作。