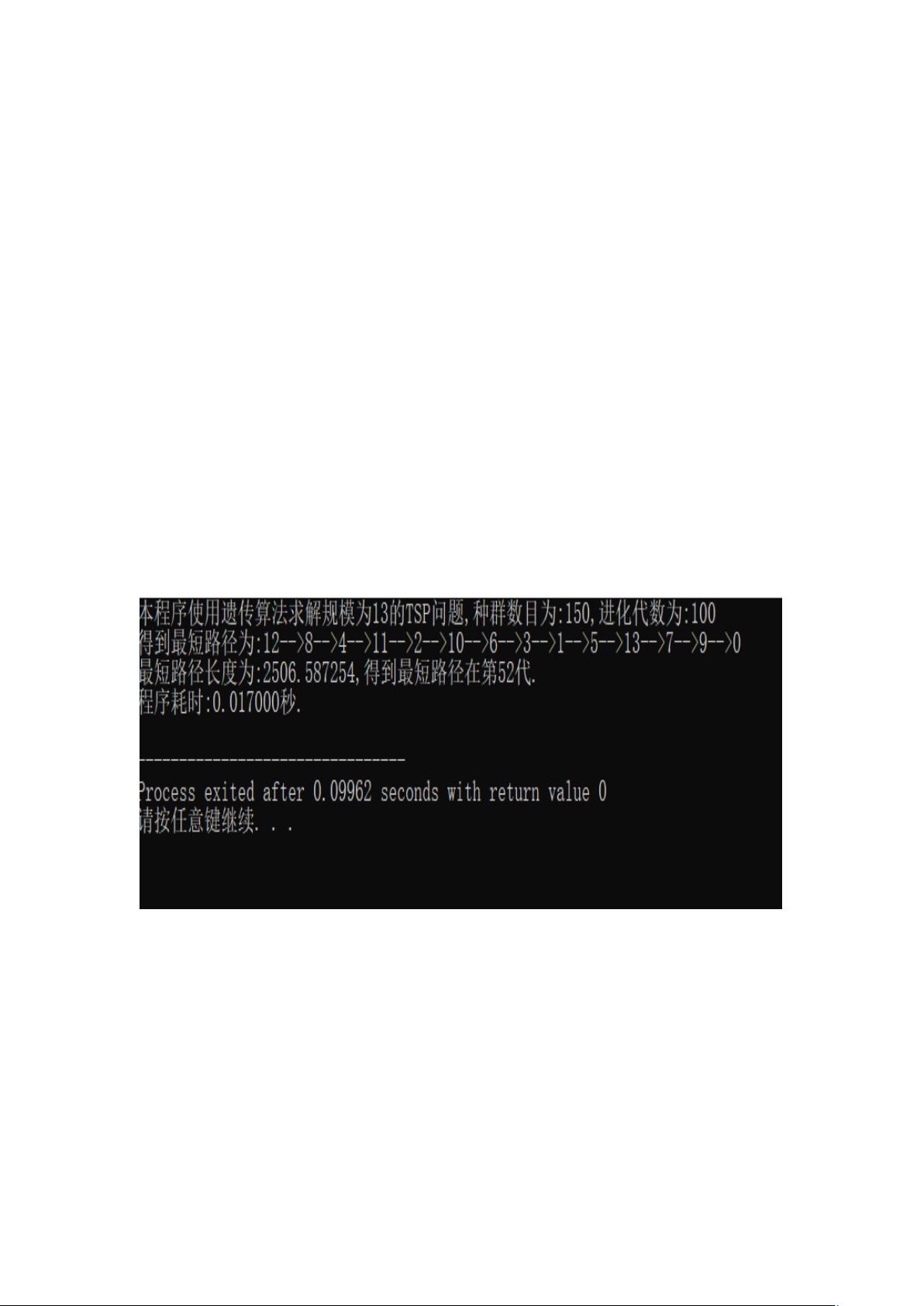
《遗传算法解决旅行商问题》 旅行商问题(TSP,Traveling Salesman Problem)是一个经典的组合优化问题,其核心是寻找一条经过所有城市恰好一次并返回起点的最短路径。遗传算法是一种模拟生物进化过程的优化算法,适用于解决此类复杂问题。 在TSP问题中,我们有n个城市,每对城市间有距离dij表示,要求旅行商从一个城市出发,遍历所有城市一次,最后返回起点,目标是最小化路径总长度。对于一个具体的实例,例如有13个城市的TSP问题,我们可以得到每个城市的坐标。通过这些坐标,我们可以计算任意两个城市之间的距离,构建距离矩阵D。 遗传算法的基本步骤包括: 1. 初始化种群:随机生成一定数量(如150)的个体,每个个体代表一个可能的路径,用一个长度为n的序列表示,序列中的数字表示访问城市的顺序。 2. 适应度评估:根据路径长度计算每个个体的适应度,通常适应度函数为路径长度的倒数,越短的路径适应度越高。 3. 选择操作:基于适应度,采用某种策略(如轮盘赌选择)选取一部分个体进入下一代。 4. 交叉操作:对选取的个体进行交叉,生成新的个体,通常采用部分匹配交叉或均匀交叉等方式。 5. 变异操作:以一定的概率(如0.008)对个体进行变异,可能改变序列中的某些元素顺序,增加解的多样性。 6. 迭代:重复步骤2-5,直到达到最大进化代数(如100代),或者找到满足条件的解。 在程序实现上,通常使用C++等编程语言编写,定义相关常量如最大进化代数、种群大小、交叉概率和变异概率。同时,需要定义城市坐标数组,以及存储种群和最佳路径的数组。在实际运行中,通过调用初始化、适应度计算、选择、交叉、变异和逆转等函数,迭代更新种群,直至找到最优解。 实验结果显示,遗传算法在第52代左右找到了最优路径。实验表明,遗传算法的效率受到编码长度(即城市个数)和变异概率的影响。合适的编码长度可以保证足够的变异多样性,而变异概率的设置则需要平衡全局搜索和局部搜索的能力,避免过早收敛或丢失最优解。 总结来说,遗传算法为解决旅行商问题提供了一种有效的方法,通过模拟自然选择和遗传机制,能够在复杂空间中搜索到近似最优解。然而,参数的选择对算法性能至关重要,需要通过多次实验和调整来找到合适的参数组合。本实验不仅展示了遗传算法的工作原理,还强调了参数优化的重要性,为今后解决类似问题提供了实践经验和理论基础。

剩余12页未读,继续阅读

- 粉丝: 1
- 资源: 4
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功