《高频电子线路第4章》主要探讨的是非线性、时变参量电路和变频器的相关理论。在电子工程中,电路可以分为线性电路和非线性电路两大类。线性电路由线性元件构成,如电阻、电容和空心电感,其特点是输出输入关系遵循线性代数方程或线性微分方程,具有叠加性和均匀性。而非线性电路则至少包含一个非线性元件,如二极管、晶体管等,它们的输出输入关系是非线性的,不满足叠加性和均匀性。
非线性电路的一个重要特性是频谱搬移,即当信号通过非线性电路后,输出信号中会产生新的频率成分,同时可能丢失原有的某些频率成分。这种特性在混频器中被广泛应用,用于改变信号的频率。线性时变电路是参数随时间变化的线性电路,例如在混频过程中,晶体管可以被视为变跨导的线性参变元件。
分析非线性电路的方法主要包括图解法和解析法。图解法是根据非线性元件的特性曲线和输入信号波形直接画图求解电流和电压波形;解析法则依赖于非线性元件特性的数学表达式,通过列出电路方程求解。例如,对于二极管的伏安特性,可以使用幂级数分析法或折线分析法。
非线性元件的三个主要特征包括:
1. 输出量与输入量之间的非线性关系。
2. 频率变换作用,这在混频器中得到体现,用于实现频率混合。
3. 不满足叠加原理,即输入信号的组合并不等同于各自独立作用的结果。
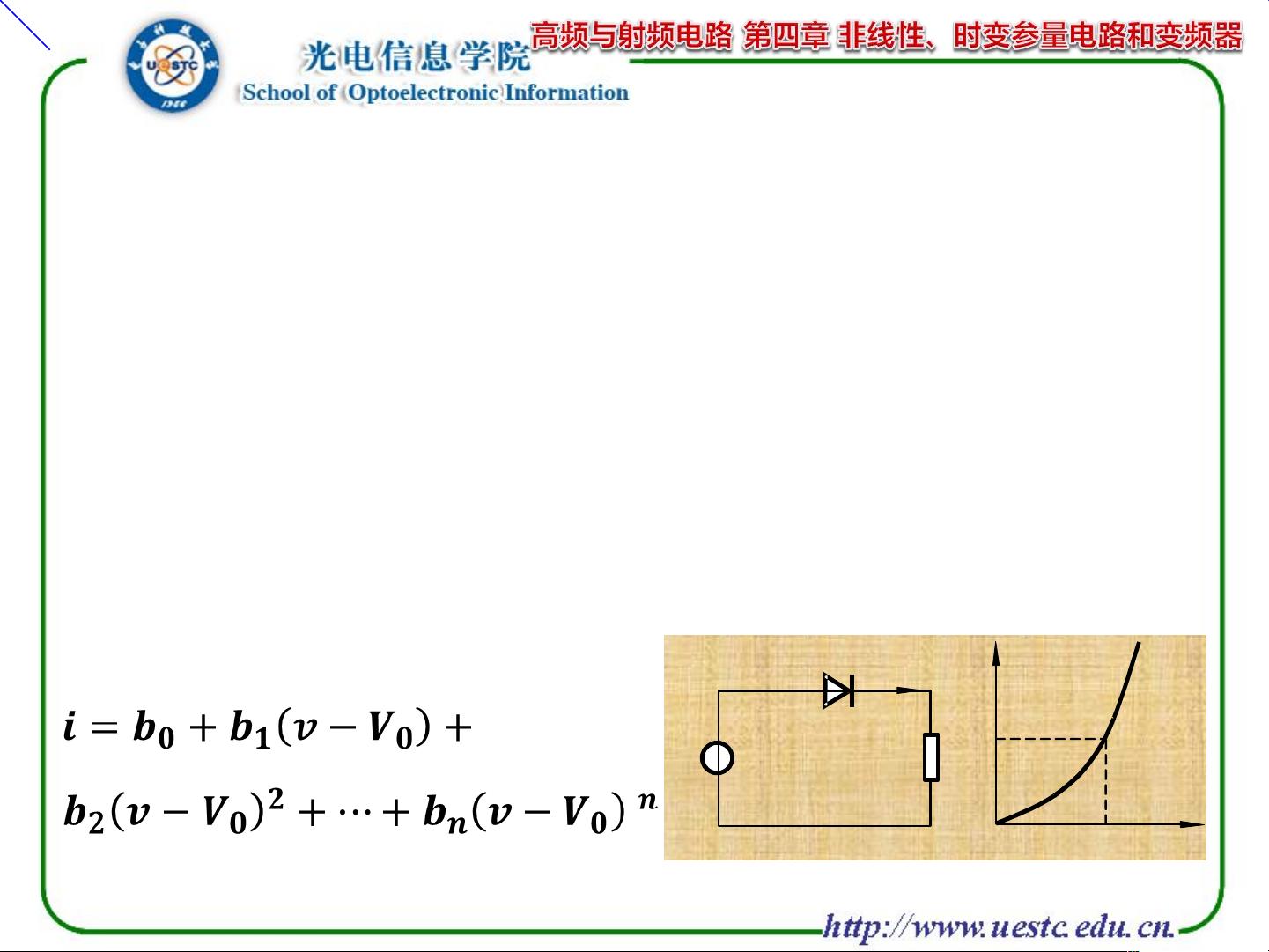
以半导体二极管为例,它是一种典型的非线性元件,其伏安特性曲线不是一条直线,静态电阻和动态电阻随工作点变化。当非线性电阻如二极管接收到正弦电压时,会产生非正弦的周期电流,导致频率变换。例如,输入信号的频率在输出信号中可能会产生倍频或分频成分。
在工程实践中,分析非线性电路通常采用幂级数法,将非线性函数在静态工作点附近展开为泰勒级数,并保留有限项进行近似。这种方法在处理一次多项式(线性近似)和二次多项式(抛物线近似)时尤为有效。
《高频电子线路第4章》涵盖了非线性电路的基本概念、特性以及分析方法,对于理解和设计涉及非线性元件的高频电子系统至关重要。这些知识不仅适用于理论研究,也是解决实际工程问题的基础。