QPSK、8PSK、16PSK以及16QAM调制下的信道容量曲线

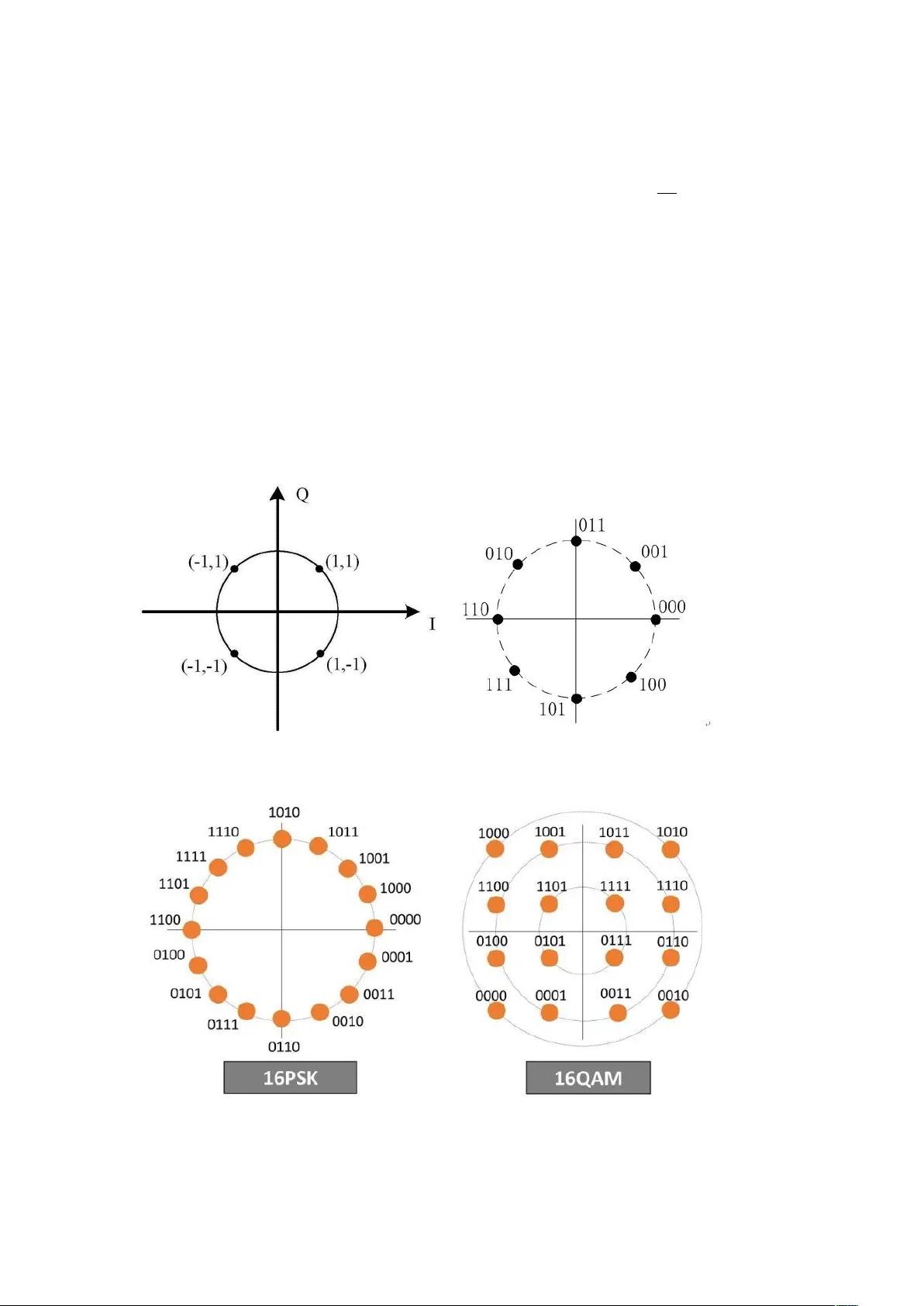
参考文献《Channel Codes: Classical and Modern》推导不同调制方式下的信道容量曲线。现在有一个二维M元信号集合，及信号的二维矢量表示。每一个信号波形都可以由完备的两个归一化正交函数的线性组合表示。现每一个都用使用复数表示。在高斯信道中二维的M进制调制的容量公式可以看成二进制情况的直接推广。word中有源代码和推导过程。matlab的m文件在下一个帖子里。 在通信领域，调制技术是传输信息的关键环节之一。本文主要探讨了在高斯信道中，使用QPSK（四相相移键控）、8PSK（八相相移键控）、16PSK（十六相相移键控）以及16QAM（十六进制幅度键控）四种调制方式时的信道容量曲线。这些调制方法常用于数字通信系统，以高效地利用有限的频谱资源。 信道容量是通信系统中一个重要的概念，它代表了在特定信道条件下，理论上能够达到的最大传输速率。在高斯信道中，二维的M进制调制的容量公式可以看作是二进制调制的直接扩展。根据香农定理，对于一个高斯白噪声信道，信道容量C可以用以下公式表示： \[ C = \frac{1}{2} \log_2(1 + \text{SNR}) \] 其中，SNR是信噪比（Signal-to-Noise Ratio），即信号功率与噪声功率之比。 在给定的描述中，作者采用了更具体的公式来计算不同调制方式下的信道容量。设二维M元信号集合中的每个信号波形可以表示为两个归一化正交函数的线性组合，使用复数表示。然后，通过计算每个信号波形在高斯信道中的概率密度函数，可以得到信道容量的表达式： \[ C = \sum_{m=1}^{M} p(m) \log_2\left(\frac{1}{p(m)}\right) \] 其中，\( p(m) \) 表示第m个信号出现的概率，而\( p(y) \)是接收端的复合概率密度函数，它由所有可能信号的概率密度函数叠加而成。噪声被假设为二维复数高斯分布，方差为\( N_0/2 \)。 在计算信道容量的过程中，需要考虑信号功率和噪声功率。信噪比(SNR)可以通过以下公式转换为功率比： \[ \text{SNR} = \frac{P_s}{P_n} = 10^{\frac{E_b}{N_0}} \] 其中，\( P_s \) 是信号功率，\( P_n \) 是噪声功率，\( E_b \) 是每个比特的能量，\( N_0 \) 是单边带噪声功率谱密度。 在MATLAB环境中，可以编写程序来模拟不同调制方式下的信道，计算信道容量，并绘制信道容量曲线。程序会遍历不同的信噪比范围，对每种调制方式的信号星座图进行采样，计算每个信号点的模值平方均值，从而获取信号的能量。噪声能量可以通过信号能量和信噪比关系得出。最终，利用信道容量公式，将SNR转换为\( E_b/N_0 \)，并绘制出信道容量与\( E_b/N_0 \)的关系曲线。 QPSK、8PSK、16PSK和16QAM调制的信号星座图分别展示了不同调制方式的信号分布，这些星座图有助于直观理解信号在复数平面上的分布，以及它们在高斯信道中受到噪声影响后的变化。 本文通过理论推导和MATLAB仿真，详细阐述了不同调制方式在高斯信道下的信道容量计算，提供了从理论到实践的完整流程，这对于理解数字通信系统的设计和优化具有重要的参考价值。