岩石蠕变特性研究、流变学、工程力学课程考试可用

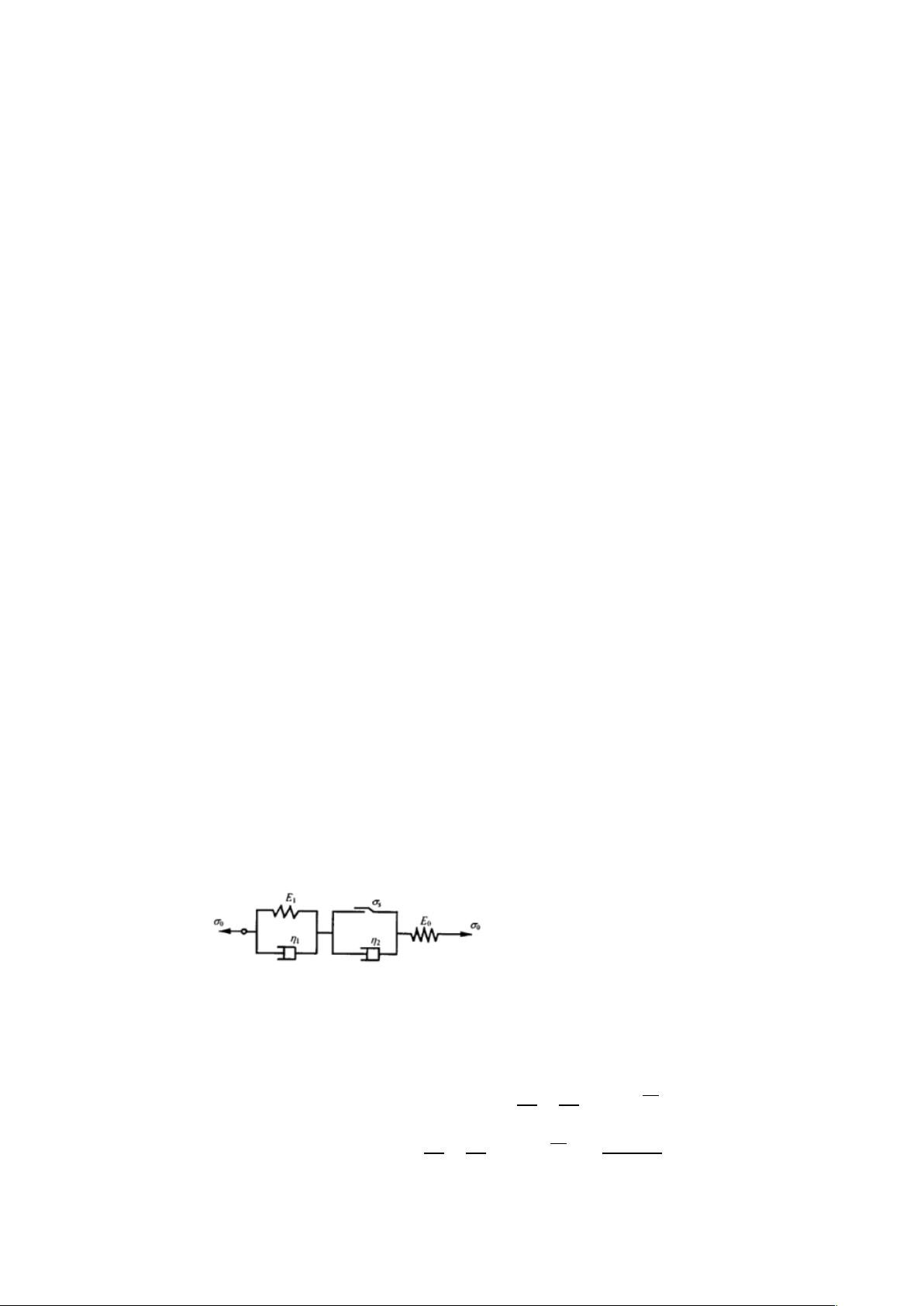
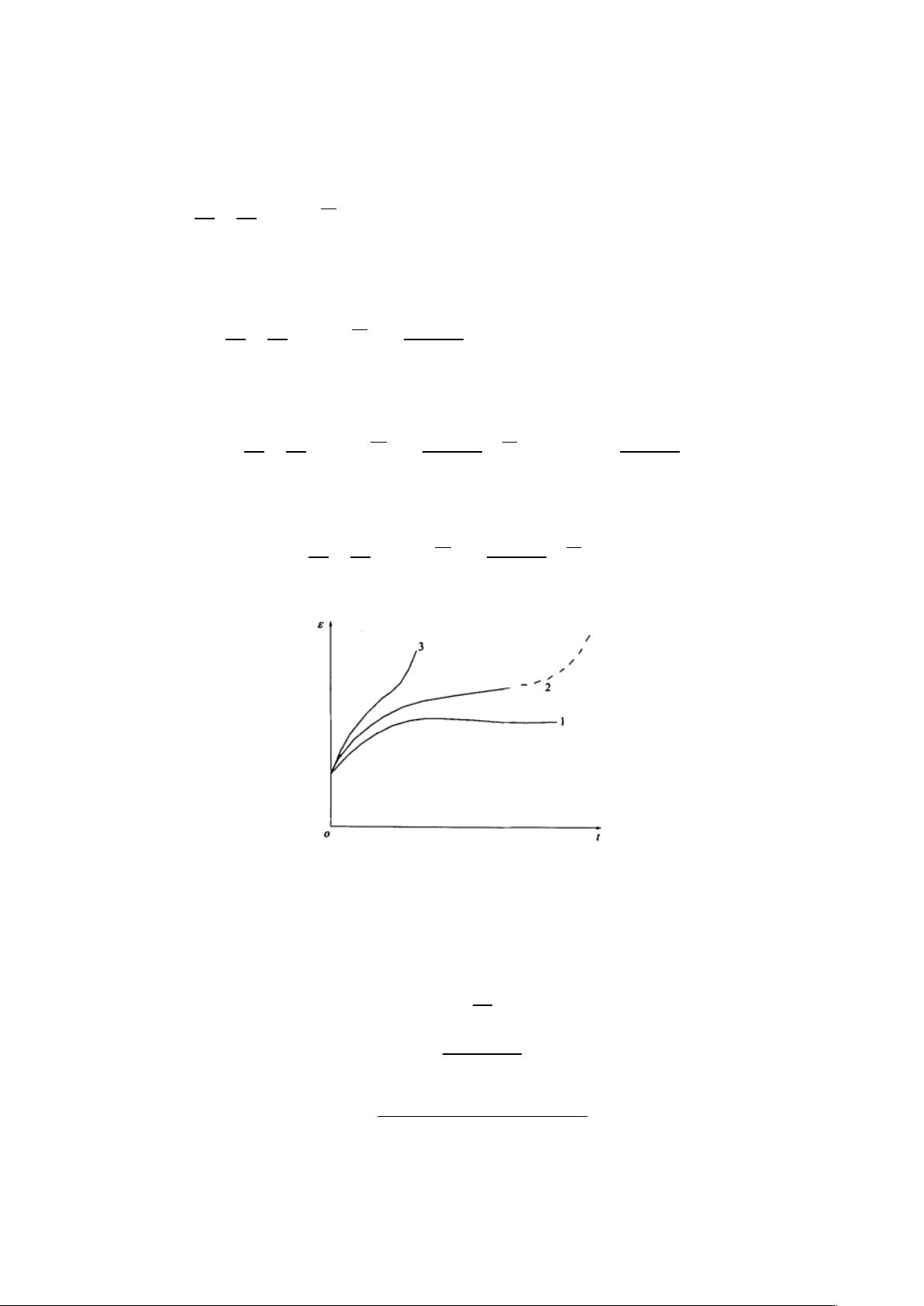
### 岩石蠕变特性研究 #### 一、引言 岩石作为一种复杂的地质体，其流变特性是重要的力学属性之一。岩石的流变特性指的是岩石在长时间受力作用下，其应力-应变状态随时间变化的现象，通常表现为蠕变行为。蠕变是指材料在恒定应力作用下持续产生应变的现象。岩石的蠕变行为不仅影响着岩石本身的稳定性，还对各类岩石工程项目的长期安全性有着重要影响。 #### 二、岩石蠕变变形全过程 岩石蠕变变形全过程可以分为三个阶段： 1. **瞬态蠕变（第一阶段）**：这一阶段又被称为过度蠕变或衰减蠕变。在这个阶段，岩石的蠕变速率较高，并且随着时间的推移而迅速减小。 2. **稳态蠕变（第二阶段）**：也称等速蠕变。在这一阶段，蠕变速率相对稳定，呈现出一个几乎恒定的速度。 3. **蠕变加速（第三阶段）**：蠕变速率再次增加，直至岩石发生破坏。 #### 三、岩石流变本构模型研究 岩石流变本构模型是描述岩石在不同应力状态下的流变特性的数学模型。这些模型可以帮助我们更好地理解和预测岩石在各种工程条件下的行为。 1. **经验流变模型** - **老化理论**：认为应力、应变和时间之间存在某种函数关系。总应变可以表示为弹性应变和蠕变应变之和。其中，\( g(t) \) 表示随着时间的增加，变形增长速度逐渐减慢，反映了材料随时间老化的特性；\( f(\sigma) \) 表示变形随应力变化的关系。 - **经验公式**： - **幂函数型**：\(\varepsilon(t) = At^n\)，其中 \( A \) 和 \( n \) 是实验常数，通常用于描述初始蠕变阶段。 - **对数型**：\(\varepsilon(t) = \varepsilon_e + B\log t + Dt\)，其中 \( B \) 和 \( D \) 为实验常数，用于描述加速蠕变阶段。 - **指数型**：\(\varepsilon(t) = A[1 - \exp(f(t))]\)，其中 \( A \) 为实验常数，\( f(t) \) 为按负数衰减的函数，用于描述等速蠕变阶段。 2. **蠕变理论模型** - **Kelvin 固体模型**：适用于低应力水平下的卸载过程，模型能够描述卸载后应变逐渐回复至零的现象。 - **三参量固体模型**：由一种基本模型和一种基本元件组成，可以组合成不同的模型。这种模型适合描述低应力水平下的蠕变行为，当 \( t \rightarrow \infty \) 时，应变趋于定值。 - **Burgers 模型**：适用于高应力水平下的蠕变行为，特别是当应力超过某一阈值 \( \sigma_s \) 时，应变不收敛，随时间逐渐增大。 - **西原模型**：结合了上述模型的优点，能够描述岩石在不同应力水平下的蠕变行为。西原模型的应力-应变-时间关系式为： - 当 \( \sigma_0 \leq \sigma_s \) 时，\(\varepsilon(t) = \frac{\sigma_0}{E_0} + \frac{\sigma_0}{E_1}(1 - e^{-\frac{E_1}{\eta_1}t})\) - 当 \( \sigma_0 > \sigma_s \) 时，\(\varepsilon(t) = \frac{\sigma_0}{E_0} + \frac{\sigma_0}{E_1}(1 - e^{-\frac{E_1}{\eta_1}t}) + (\sigma_0 - \sigma_s)\frac{t}{\eta_2}\) #### 四、结论 岩石的蠕变行为是岩石力学研究中的一个重要方面，对于评估岩石工程项目的长期稳定性和安全性至关重要。通过对岩石蠕变特性的深入研究，我们可以更准确地预测岩石在各种工程条件下的行为，从而提高工程设计的安全性和经济性。此外，开发更为精确和实用的岩石流变本构模型仍然是当前岩石力学领域的一个重要研究方向。