# Stacking
## 简述
主要的三类集成学习方法为**Bagging、Boosting和Stacking**。目前，大型的数据挖掘比赛（如Kaggle），排名靠前的基本上都是集成机器学习模型或者深度神经网络。
将训练好的所有基模型对整个训练集进行预测，第$j$个基模型对第i个训练样本的预测值将作为新的训练集中第$i$个样本的第$j$个特征值，最后基于新的训练集进行训练。同理，预测的过程也要先经过所有基模型的预测形成新的测试集，最后再对测试集进行预测。
具体原理讲解参考[这篇博客](https://blog.csdn.net/wstcjf/article/details/77989963)，简单来说，集成学习其实都是将基本模型组合形成更优秀的模型，Stacking也不例外。stacking是得到各个算法训练全样本的结果再用一个元算法融合这些结果，它可以选择使用网格搜索和交叉验证。
## Mlxtend框架
> 众所周知，如今传统机器学习领域的库基本上被sciket-learn（sklearn)占领，若你没有使用过sklearn库，那就不能称为使用过机器学习算法进行数据挖掘。但是，**自定义集成学习库依然没有什么太过主流的框架**，sklearn也只是实现了一些比较主流的集成学习方法如随机森林（RF）、AdaBoost等。当然，这也是因为bagging和boosting可以直接调用而stacking需要自己设计。
Mlxtend完美兼容sklearn，可以使用sklearn的模型进行组合生成新模型。它同时集成了stacking分类和回归模型以及它们的交叉验证的版本。由于已经有很多stacking的分类介绍，本例以回归为例讲讲stacking的回归实现。
### Mlxtend安装
`pip install mlxtend`
### 官方文档
[地址](http://rasbt.github.io/mlxtend/)
## 项目实战
### stacking回归
stacking回归是一种通过元回归器（meta-regressor）组合多个回归模型（lr，svr等）的集成学习技术。而且，每个基回归模型（就是上述的多个回归模型）在训练时都要**使用完整训练集**，集成学习过程中每个基回归模型的输出作为元特征成为元回归器的输入，元回归器通过拟合这些元特征来组合多个模型。
### 使用StackingRegressor
简单使用stacking模型预测波士顿房价（使用经典波士顿房价数据集）由于大数据集需要精细调参，这里简单使用100条数据进行回归测试。
```python
from mlxtend.regressor import StackingRegressor
from mlxtend.data import boston_housing_data
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt
x, y = boston_housing_data()
x = x[:100]
y = y[:100]
# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# 初始化基模型
lr = LinearRegression()
svr_lin = SVR(kernel='linear', gamma='auto')
svr_rbf = SVR(kernel='rbf', gamma='auto')
ridge = Ridge(random_state=2019)
models = [lr, svr_lin, svr_rbf, ridge]
print('base model')
for model in models:
model.fit(x_train, y_train)
pred = model.predict(x_test)
print("loss is {}".format(mean_squared_error(y_test, pred)))
sclf = StackingRegressor(regressors=models, meta_regressor=ridge)
# 训练回归器
sclf.fit(x_train, y_train)
pred = sclf.predict(x_test)
print('stacking model')
print("loss is {}".format(mean_squared_error(y_test, pred)))
plt.scatter(np.arange(len(pred)), pred)
plt.plot(np.arange(len(y_test)), y_test)
plt.show()
```
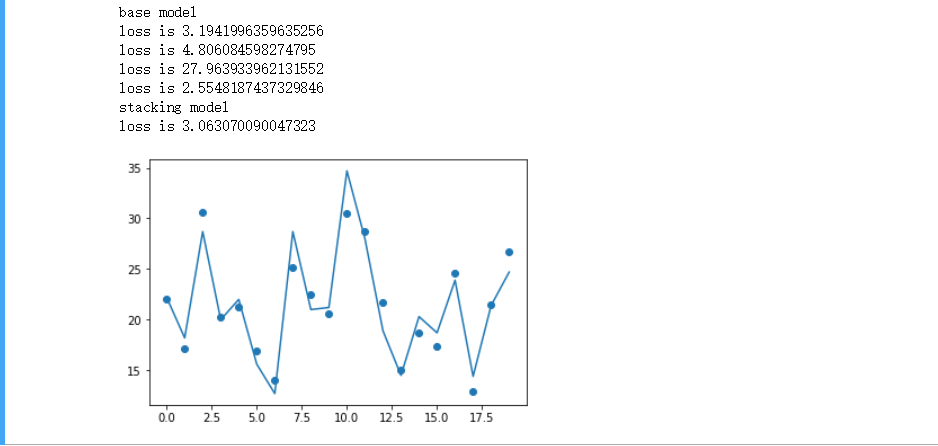
可以看到stacking模型的一般预测准确率是高于所有基模型的。
### 对stacking模型网格搜索调参
这里仍然使用上一个案例的模型，下面是代码及结果。
```python
from mlxtend.regressor import StackingRegressor
from mlxtend.data import boston_housing_data
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt
x, y = boston_housing_data()
x = x[:100]
y = y[:100]
# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# 初始化基模型
lr = LinearRegression()
svr_lin = SVR(kernel='linear', gamma='auto')
svr_rbf = SVR(kernel='rbf', gamma='auto')
ridge = Ridge(random_state=2019,)
models = [lr, svr_lin, svr_rbf, ridge]
params = {
'ridge__alpha': [0.1, 1.0, 10.0],
}
sclf = StackingRegressor(regressors=models, meta_regressor=ridge)
# 训练回归器
grid = GridSearchCV(estimator=sclf, param_grid=params, cv=5, refit=True)
grid.fit(x_train, y_train)
print(grid.best_params_, grid.best_score_)
```
### 使用StackingCVRegressor
mlxtend.regressor中的StackingCVRegressor是一种集成学习元回归器。StackingCVRegressor扩展了标准Stacking算法（在mlxtend中的实现为StackingRegressor）。在标准Stacking算法中，拟合一级回归器的时候，我们如果使用与第二级回归器的输入的同一个训练集，这很可能会导致过拟合。 然而，StackingCVRegressor使用了"非折叠预测"的概念:数据集被分成k个折叠，并且在k个连续的循环中，使用k-1折来拟合第一级回归器，其实也就是k折交叉验证的StackingRegressor。在K轮中每一轮中，一级回归器被应用于在每次迭代中还未用于模型拟合的剩余1个子集。然后将得到的预测叠加起来并作为输入数据提供给二级回归器。在StackingCVRegressor的训练完成之后，一级回归器拟合整个数据集以获得最佳预测。
```python
from mlxtend.regressor import StackingCVRegressor
from mlxtend.data import boston_housing_data
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_score
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt
x, y = boston_housing_data()
x = x[:100]
y = y[:100]
# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# 初始化基模型
lr = LinearRegression()
svr_lin = SVR(kernel='linear', gamma='auto')
ridge = Ridge(random_state=2019,)
lasso =Lasso()
models = [lr, svr_lin, ridge, lasso]
print("base model")
for model in models:
score = cross_val_score(model, x_train, y_train, cv=5)
print(score.mean(), "+/-", score.std())
sclf = StackingCVRegressor(regressors=models, meta_regressor=lasso)
# 训练回归器
print("stacking model")
score = cross_val_score(sclf, x_train, y_train, cv=5)
print(score.mean(), "+/-", score.std())
sclf.fit(x_train, y_train)
pred = sclf.predict(x_test)
print("loss is {}".format(mean_squared_error(y_test, pred)))
```
)
可以看到，对比第一次使用StackingRegressor模型的损失降低了。（尽管由于调参问题，评分没有基回归器高）
### 使用StackingCVRegressor网格搜索
代码及结果如下。
```python
from mlxtend.regressor import StackingCVRegressor
from mlxtend.data import boston_housing_data
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_score
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt
x, y = boston_housing_data()
x = x[:100]
y = y[:100]
# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# 初始化基模型
lr = LinearRegression()
svr_lin = SVR(kernel='
