Variance Functions:
Constant:
1
Power:
X
2
Binomial:
np(1 − p)
where
p =
µ
n
; V (µ) = np(1 − p)
Links: initialization of base class returns
µ
;
p
in the logit and subclasses;
x
elsewhere.
Link
g(p)
Inverse
g
−1
(p)
Analytic Derivative
g
0
(p)
Logit
z = log
p
1−p
p =
e
z
1+e
z
g
0
(p) =
1
p(1−p)
Power
z = x
pow
x = z
1
pow
g
0
(x) =
pow
· x
power
−1
Inverse same as above with pow
= −1
Square Root pow
= 0.5
Identity pow
= 1
Log
z = log x g
−1
(z) = e
z
g
0
(x) =
1
x
CDFLink/Probit
z = Φ
−1
(p) p = Φ(z) g
0
(x) =
1
´
p
−∞
f(t)dt
Cauchy same as the above with the Cauchy distribution
CLogLog
z = log(− log p) p = e
−e
z
g
0
(p) = −
1
p log p
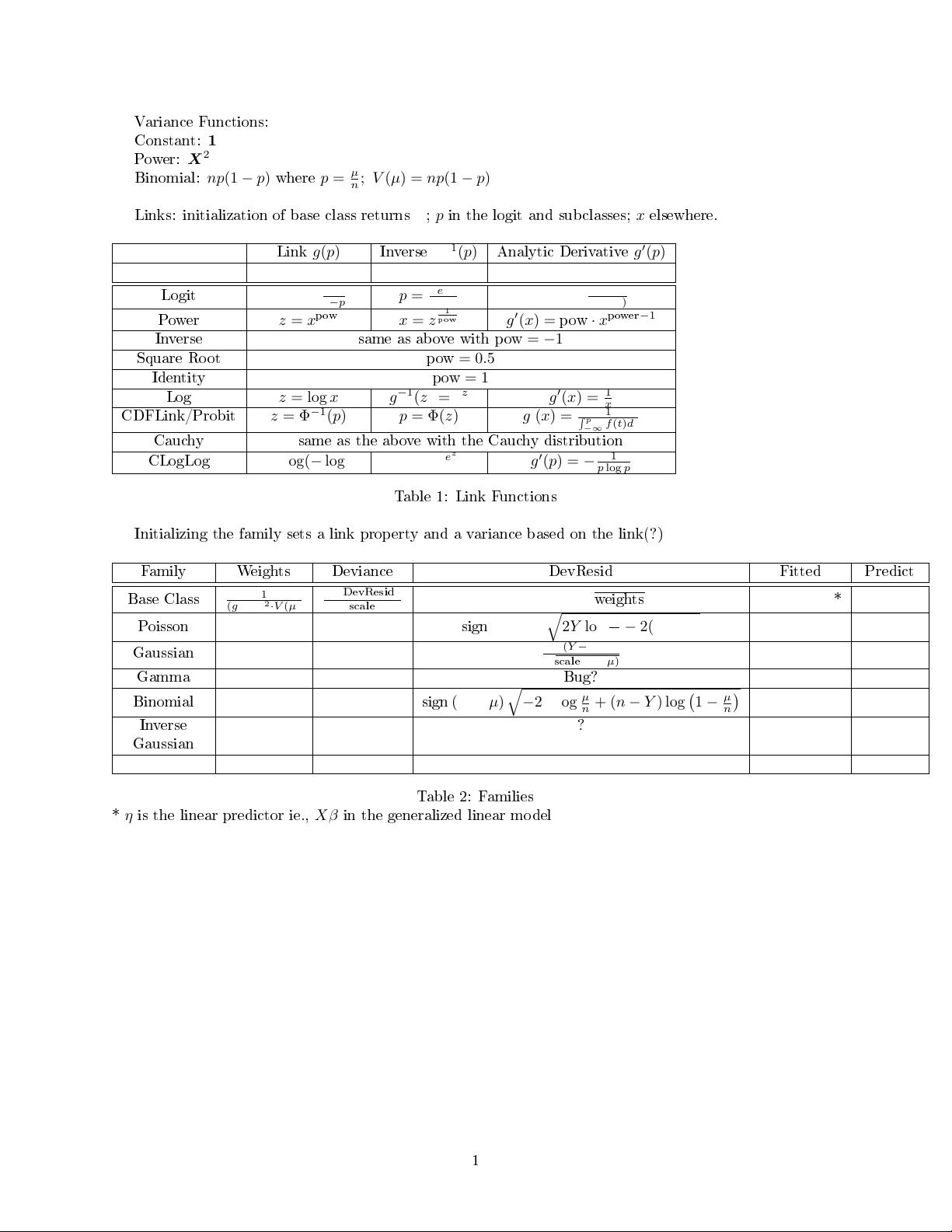
Table 1: Link Functions
Initializing the family sets a link property and a variance based on the link(?)
Family Weights Deviance DevResid Fitted Predict
Base Class
1
(g
0
(µ))
2
·V (µ)
P
i
DevResid
2
scale
(Y − µ) ·
√
weights
µ = g
−1
(η)
*
η = g(µ)
Poisson sign
(Y − µ)
q
2Y log
Y
µ
− 2(Y − µ)
Gaussian
(Y −µ)
p
scale
· V (µ)
Gamma Bug?
Binomial sign
(Y − µ)
q
−2Y log
µ
n
+ (n − Y ) log
1 −
µ
n
Inverse
Gaussian
?
Table 2: Families
*
η
is the linear predictor ie.,
Xβ
in the generalized linear model
1















