动态规划解决电路排线问题

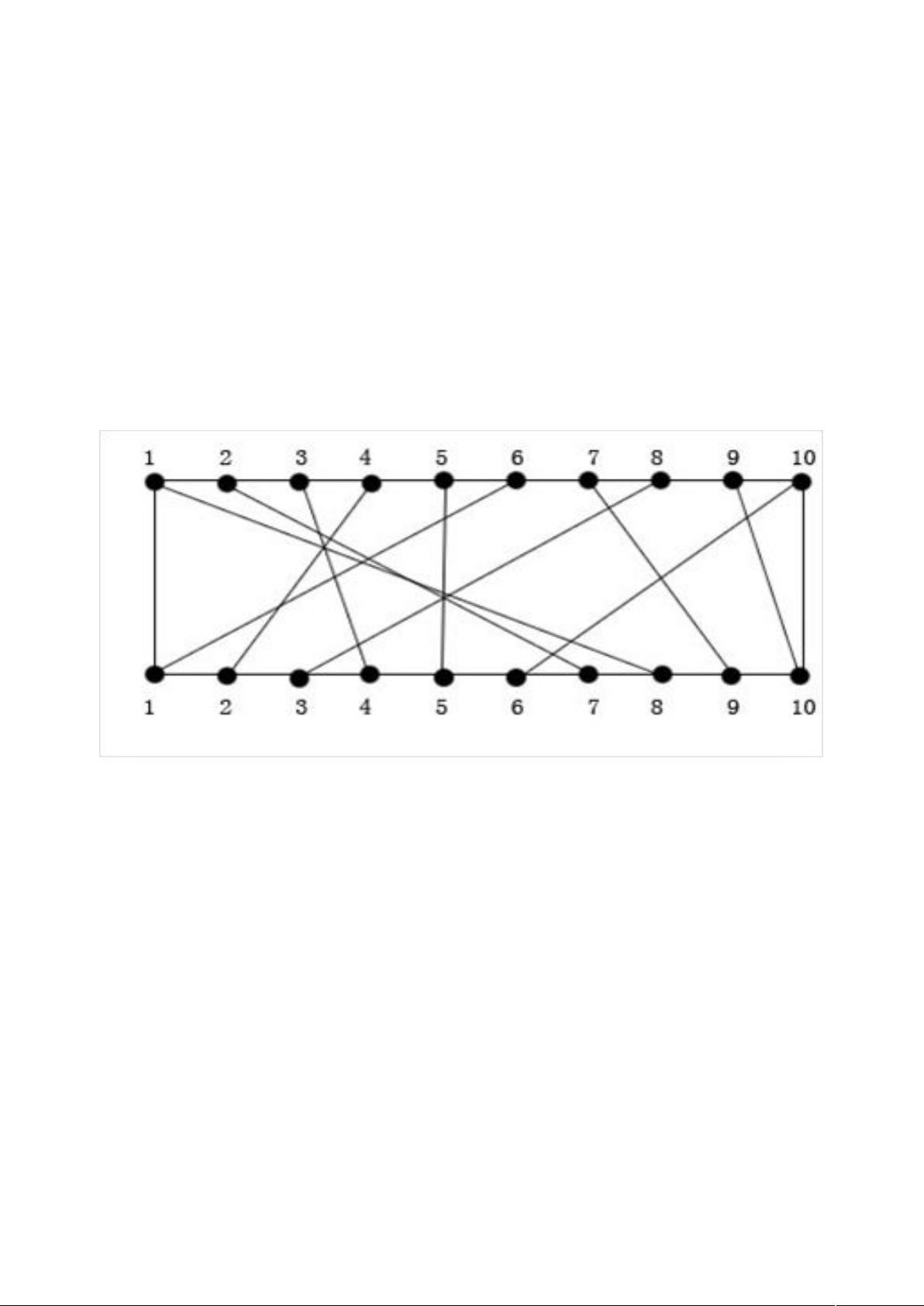
动态规划是一种解决问题的有效方法，尤其在处理具有重叠子问题和最优子结构的复杂问题时。在这个特定的电路排线问题中，我们需要找到一个电路板上导线的最大不相交子集，使得这些导线可以在同一绝缘层上布置，而不会相互交叉。问题的关键在于如何利用动态规划的思路来构建解决方案。 1. **问题描述**： 在电路板的上下两端各有n个接线柱，用导线(i,π(i))连接对应的上下接线柱。导线(i,π(i))与导线(j,π(j))相交的条件是π(i)>π(j)。目标是确定一个最大的导线子集，它们在同一层上互不相交。 2. **最优子结构性质**： 这个性质是动态规划的基础，意味着问题的最优解可以通过其子问题的最优解来构建。在这个电路布线问题中，我们定义N(i,j)为集合{t | (t, π(t)) 属于 Nets, t ≤ i, π(t) ≤ j}。MNS(i,j)表示N(i,j)中的最大不相交子集的大小，即Size(i,j)。通过对i和j的不同取值，我们可以分析出MNS(i,j)与MNS(i-1,j)或MNS(i-1,π(i)-1)的关系，从而得到递推公式。 3. **递推关系**： 动态规划的解决方案通常涉及自底向上的计算过程。在这个问题中，我们首先计算只有1个、2个接线柱的最优布线，然后逐渐增加接线柱的数量，计算更复杂的布线情况。代码中，`MNS`函数用于计算子问题的最优值，而`Traceback`函数则用于回溯找到最优解的具体元素。 4. **代码实现**： C++代码展示了如何应用动态规划来解决这个问题。数组`C`存储了π(i)的值，`size`数组用于存储每个子问题的最优解大小。`MNS`函数执行递推计算，`Traceback`函数则根据`size`数组回溯找出最大不相交子集。 5. **算法流程**： - 初始化二维数组`size`，用于存储每个子问题的解。 - 从最简单的子问题开始，即只有一个接线柱的情况，逐步计算更复杂的情况。 - 对于每个子问题(i, j)，根据最优子结构性质计算Size(i,j)。 - 使用回溯法从`size`数组中恢复最大不相交子集，并输出结果。 总结起来，这个电路排线问题通过动态规划的方法，利用最优子结构性质和递推关系，能够有效地找到一个电路板上最大数量的不相交导线子集，从而解决了电路布线的优化问题。这个例子展示了动态规划在实际问题中的应用，以及如何通过编程实现这一策略。