在区间集决策系统中基于双粒化和三视角不确定性度量的系统性属性约简资源-CSDN文库

论文

属性约简

73 浏览量 2024-10-06 09:29:39 上传评论收藏 4.96MB PDF 举报

资源推荐

资源详情

资源评论

Systematic attribute reductions based on double granulation structures and

three-view uncertainty measures in interval-set decision systems

Xin Xie

a,b

, Xianyong Zhang

a,b,c,∗

School of Mathematical Sciences, Sichuan Normal University, Chengdu 610066, China

Institute of Intelligent Information and Quantum Information, Sichuan Normal University, Chengdu 610066, China

Visual Computing and Virtual Reality Key Laboratory of SiChuan Province, Sichuan Normal University, Chengdu 610066, China

Abstract

Attribute reductions eliminate redundant information to become valuable in data reasoning. In the data context of

interval-set decision systems (ISDSs), attribute reductions rely on granulation structures and uncertainty measures;

however, the current structures and measures exhibit the singleness limitations, so their enrichments imply corre-

sponding improvements of attribute reductions. Aiming at ISDSs, a fuzzy-equivalent granulation structure is proposed

to improve the existing similar granulation structure, dependency degrees are proposed to enrich the existing condition

entropy by using algebra-information fusion, so 3×2 attribute reductions are systematically formulated to contain both

a basic reduction algorithm (called CAR) and ﬁve advanced reduction algorithms. At the granulation level, the similar

granulation structure is improved to the fuzzy-equivalent granulation structure by removing the granular repeatability,

and two knowledge structures emerge. At the measurement level, dependency degrees are proposed from the algebra

perspective to supplement the condition entropy from the information perspective, and mixed measures are gener-

ated by fusing dependency degrees and condition entropies from the algebra-information viewpoint, so three-view

and three-way uncertainty measures emerge to acquire granulation monotonicity/non-monotonicity. At the reduction

level, the two granulation structures and three-view uncertainty measures two-dimensionally produce 3×2 heuristic re-

duction algorithms based on attribute signiﬁcances, and thus ﬁve new algorithms emerge to improve an old algorithm

(i.e., CAR). As ﬁnally shown by data experiments, 3 × 2-systematic construction measures and attribute reductions

exhibit the eﬀectiveness and development, comparative results validate the three-level improvements of granulation

structures, uncertainty measures, and reduction algorithms on ISDSs. This study resorts to tri-level thinking to enrich

the theory and application of three-way decision.

Keywords: Attribute reduction; Interval-set decision system; Granulation structure; Uncertainty measure; Condition

entropy; Granulation monotonicity/non-monotonicity

1. Introduction

Attribute reductions in rough set theory are related to feature selections in machine learning, and they mainly

reduce data dimensionality to facilitate information processing and knowledge discovery [1]. Attribute reductions

have various approaches, especially on classiﬁcation tasks and learning [2, 3, 4, 5, 6, 7, 8, 9]. Attribute reductions

have become a fundamental research topic, and they are extensively applied in multiple ﬁelds such as formal concept

analysis [10, 11, 12].

Rough set theory explores data reasoning, and thus it relies on decision systems with data representations. Tra-

ditionally, attribute values of samples are single-valued, so single-valued decision systems (SVDSs) are mainly em-

ployed to multiple generic environments [13, 14, 15, 16, 17]. In practical scenarios, attribute values are often uncer-

tain or fuzzy, so they can exhibit interval-based forms. Accordingly, Yao [18] introduced interval sets, and relevant

concepts based on interval sets (including interval-set information tables (ISITs) and interval-set decision systems

(ISDSs) [19]) gained continuous research. For example, Zhong and Huang [20] analyzed granulation structures of

interval sets from measure and set; Lin et al. [21] introduced the conjunction form and dominance relation in ISITs;

Li et al. [22] discussed the concept representation and rule induction in incomplete ISITs; Wang [23] gave the fuzzy

∗

Corresponding author

Email addresses: 702374273@qq.com (Xin Xie), xianyongzh@sina.com.cn (Xianyong Zhang )

Preprint submitted to International Journal of Approximate Reasoning May 5, 2024

preference relation in ISITs; Zhang et al. [24] discussed the uncertainty measurement in ISITs; recently, attribute

reduction algorithms in ISDSs got some discussions [25, 26, 27, 28]. Clearly, ISDSs have the signiﬁcance of data

learning; however, their attribute reductions and corresponding heuristic algorithms are relatively rare, so are worth

advancing for better approximate reasoning. ISDSs-driven attribute reductions usually rely on granulation structures

and uncertainty measures, and thus the two aspects are next analyzed to induce the corresponding enrichments and

improvements of attribute reductions.

(a) Similar granulation structure (b) Fuzzy-equivalent granulation structure

Figure 1: Two granulation structures on interval-set decision system.

Aiming at ISDSs, the sample granulation is fundamental, and it usually relies on the object similarity [24, 26]. In

recent studies, sample similarity functions are primarily developed, and they further generate the similar granulation

structure. This granulation method formulates a sample partition structure that accurately traces the sample’s location,

but it also carries two limitations for further advancement.

• The similar granulation structure may contain repeated granules sometimes. As shown in Fig. 1(a) with circle

labels of similarity classes, the classes of samples x

, x

are the same {x

, x

}, so including all the

three samples in the granulation structure would involve the granule {x

, x

} three times. The granular

redundancy easily causes the information deviation to impact uncertainty measurement.

• The similar granulation structure may contain diﬀerent granules with the same overlapping sample, and this

case leads to the duplicate counting of the same sample. As shown in Fig. 1(a), sample x

has a similarity

class {x

, x

}, while sample x

has a similarity class {x

, x

}; although {x

, x

} and

, x

} are diﬀerent, including them in a granular structure would produce the double counting of samples

, x

. The overlap redundancy is not conducive for information optimization and accurate measurement.

This paper ﬁrst addresses the two issues from similar granulation structure, and we propose a new structure based

on fuzzy similarity relation, called the fuzzy-equivalent granulation structure. As shown in Fig. 1(b), we eventu-

ally present the new structure {{x

}, {x

, x

}} in terms of similarity classes G

, G

in Fig. 1(a),

and the three granules {x

}, {x

, x

} have advantages of non-repetition and non-overlap to improve the initial

similarity-granular structure, i.e., {G

, G

} in Fig. 1(a). In other words, the fuzzy-equivalent granu-

lation structure can eliminate the two redundancy problems (related to granule repetition and sample interaction) of

similar granulation structure, and thus its consequent informatization and measurement would have the corresponding

superiority.

Uncertainty measures based on knowledge granulation play a crucial role in rough learning, and their various

forms are utilized for attribute reductions [29, 30, 31, 32]. In particular, algebraic and informational measures adhere

to uncertainty modeling and information theory, and their heterogeneous fusion can induce the powerful measurement

reinforcement and eﬃcient reduction algorithm [33, 34, 35]. For instance, Jiang et al. [36] proposed the relative

decision entropy on attribute dependency degree for feature reduction, Wang et al. [37] introduced neighborhood

self-information on approximation accuracy for attribute reduction, Xu et al. [38] fused the neighborhood credibil-

ity/coverage and neighborhood joint entropy to improve attribute reductions. In terms of ISDSs, uncertainty measures

also facilitate attribute reductions. Recent attribute reductions in [25, 26, 27, 28] resort to only a single form of alge-

braic and informational measures; more generally, the fused uncertainty measures and improved reduction algorithms

are rarely concerned, so they become a valuable topic. This paper later focuses on ISDSs-driven attribute reductions

and heuristic algorithms by measure fusion and reduct enrichment. In [26], a condition entropy is proposed by modi-

fying the classical condition entropy in [39], and this information measure induces an eﬀective algorithm of attribute

reduction, called CAR. For metric and algorithmic enrichments, we will introduce the algebraic dependency γ to

combine the condition entropy H to produce an algebraic-informational measure (1 − γ)H (called the mixed condition

entropy), and thus three-view uncertainty measures H, γ, (1 − γ)H emerge to further formulate three-view attribute

reductions for learning development and classiﬁcation improvement.

？Fuzzy equivalent granulation structure (

)

？Three-way

algebra measures:

Fusion

？Three-way

information measures

√ Similar granulation structure ( )

√ CAR

√ Existing result

? ECAR

？

EDAR

？

EMAR

？

DAR

？

MAR

？New content

？Three-way mixed

conditional entropies:

√ Conditional entropy

？Attribute monotonicity,

Radius monotonicity

Attribute reduction

algorithms

Three-view

uncertainty

measures

Granulation

monotonicity/

non-monotonicity

Algebraic

view

Information

view

Granulation structures

Mixed

view

？Dependency

Improve

？Dependency-mixed

conditional entropy

？Attribute monotonicity,

Threshold non-monotonicity

Fusion

Figure 2: Research framework on granulation structures, uncertainty measures, and attribute reductions.

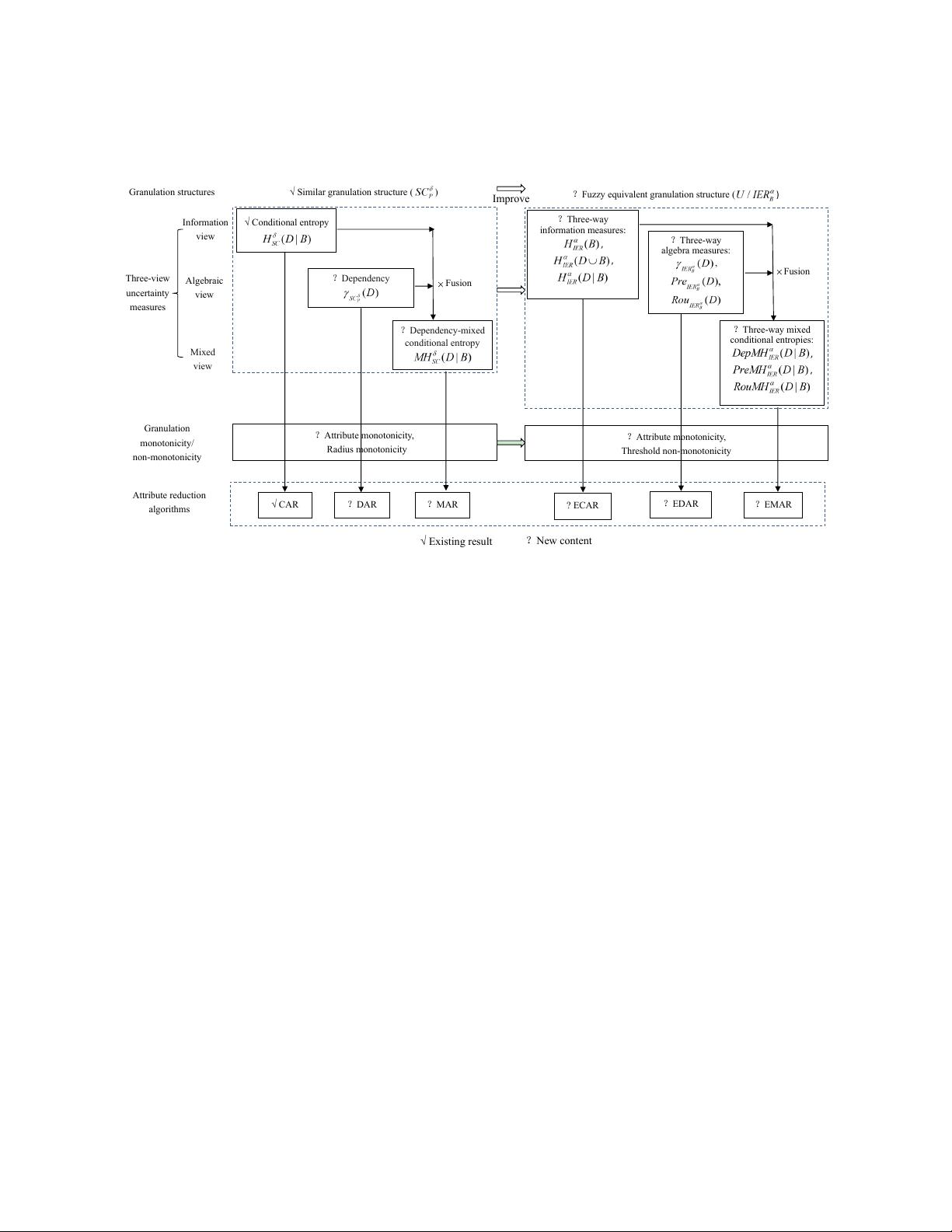
According to the above backgrounds and thoughts, this paper mainly makes three-level improvements of gran-

ulation structures, uncertainty measures, and attribute reductions in terms of ISDSs, and our research framework is

reﬂected by Fig. 2, which has more details for measure construction.

(1) Regarding ISDSs, the existing similar granulation structure has the two redundancy problems (related to gran-

ule repetition and sample interaction), and the fuzzy-equivalent granulation structure is proposed to make corre-

sponding improvements, as demonstrated and analyzed from Fig. 1 (especially its subﬁgure (b)). Thus, there are

two granulation structures, and the new mode can be calculated by a corresponding algorithm (i.e., Algorithm

2).

(2) The dependency degree is used to match the existing condition entropy in [26], and thus the fusion measure

is generated by the multiplication operator. There are three uncertainty measures from the algebraic, informa-

tional, and algebraic-informational viewpoints. Thus, three-view uncertainty measures emerge with relevant

algorithms (i.e., Algorithms 1 and 3), and their granulation monotonicity/non-monotonicity on attribute subsets

and parameter thresholds are researched and revealed.

(3) The above two-granulation structures and three-view measures are combined to induce 3 × 2 uncertainty mea-

sures, and the latter further motivate attribute reductions and corresponding heuristic algorithms within the

3 × 2 = 6 framework. Thus, two structural reducts and six metric reducts are deﬁned, and their relationships of

strongness derivation and intersection interaction are revealed. In terms of metric signiﬁcance, six reduction al-

gorithms are systematically established (in Algorithm 4), and they contain both the current algorithm CAR [26]

and ﬁve novel reduction algorithms (called DAR, MAR, ECAR, EDAR, EMAR). The new reduction algorithms

enrich and improve CAR.

(4) At last, data experiments are performed to verify the three-level improvements, so that the new granulation

structures, uncertainty measures, and attribute reductions all exhibit the eﬀectiveness. In particular, the ﬁve im-

proved reduction algorithms generally outperform the contrastive algorithm CAR to acquire better classiﬁcation

performances.

Three-way decision is an important methodology with Triading-Acting-Optimizing [40], and it relies on three-level

thinking [41] to provide three-level analysis [42] and corresponding supports. Aiming at ISDSs, three-level improve-

ments of granulation structures, uncertainty measures, and attribute reductions ﬁrst fall into the existing framework

of three-level thinking and analysis [41, 42, 43, 44], and the corresponding contributions then bring new hierarchical

development especially for three-level uncertainty measures and attribute reductions. This study adheres to three-level

thinking and analysis, so it could enrich the theory and application of three-way decision.

The remaining of this paper on ISDSs is organized as follows. Section 2 reviews the similar granulation struc-

ture, and combines the mixed condition entropy. Section 3 proposes the fuzzy-equivalent granulation structure, and

correspondingly constructs three-view uncertainty measures. Section 4 determines systematic attribute reductions

and six corresponding heuristic reduction algorithms. Section 5 performs data experiments to make the eﬀectiveness

validation and superiority comparison. Section 6 ﬁnally concludes this study.

2. Three-view uncertainty measures based on similar granulation structure

In real-life scenarios, information is often incomplete, and sample-value descriptions usually resort to upper and

lower bounds. Therefore, concepts of interval sets are initially proposed by Yao [18] and are further reﬁned by Zhang

et al. [24]. In this section, the relevant formal context of ISDSs is reviewed to oﬀer the similar granulation structure,

and the corresponding three-view uncertainty measures are formulated by proposing a mixed conditional entropy.

2.1. Similar granulation structure on ISDSs

Herein, ISDS and its basic similar granulation structure are successively recalled.

Deﬁnition 1 (ISDS [24]). An interval set, denoted as A =

[

, A

]

A ∈ 2

| A

⊆ A ⊆ A

, is a set where A

and

are subsets of a reference set U. The lower boundary set of A is A

and the upper boundary set is A

. If A

= A

then A is an ordinary set.

Based on the deﬁnition of interval sets, we can formulate ISDS implying the interval-set decision system/table.

IS DS = (U, C

D, V, f ) is a four-tuple group. Here, U = {x

, x

, · · · , x

} = {x

| i = 1, 2, · · · , n} is a ﬁnite nonempty

set of universe, C =



, a

, · · · , a

|C|



is a ﬁnite nonempty set of condition attributes, D = {d} is related to a decision

attribute d, V=

a∈A⊆C

represents the set of attribute values (where V

is a nonempty set of values for a ∈ C), and

f : U × A → V (A ⊆ C) is an information function. In particular, the value of sample x ∈ U under condition attribute

a ∈ A ⊆ C is an interval set, i.e. f (x, a) =



−

, x



with x

−

⊆ x

, x

−

⊆ V

, x

⊆ V

Example 1. For illustrations, two ISDSs in [24] are introduced in Tables 1 and 2, and they are symbolic and numerical

types, respectively.

Table 1: An interval-set decision table in symbolic form [24].

U Listening Speaking Reading Writing Excellent

[{C, S }, {E, C, S }] [{E}, {E, C, S }] [{C, S }, {C, S , F}] [{E, S }, {E, C, S }] Yes

[{C, S }, {C, S, F}] [{S }, {S, F}] [{S, F}, {C, S , F}] [{C, S }, {C, S }] Yes

[{C}, {C, S }] [{S }, {S, F}] [{F}, {S, F}] [{E, S }, {E, C, S }] No

[{C}, {C, F}] [{S }, {S, F}] [{S }, {S }] [{C, S }, {C, S }] No

[{S }, {S, F}] [{F}, {C, F}] [{E}, {E, S }] [{C, S }, {C, S }] Yes

[{S }, {S }] [{S }, {C, S }] [{C, S }, {C, S }] [{C, S }, {C, S }] No

Table 2: An interval-set decision system in numerical form [24].

U a

[{0}, {0, 1, 2}] [{1, 2}, {1, 2, 3}] [{0, 2}, {0, 1, 2}] 1

[{2}, {2, 3}] [{2, 3}, {1, 2, 3}] [{1, 2}, {1, 2}] 1

[{2}, {2, 3}] [{3}, {2, 3}] [{0, 2}, {0, 1, 2}] 2

[{2}, {2, 3}] [{2}, {2}] [{1, 2}, {1, 2}] 2

[{3}, {1, 3}] [{0}, {0, 2}] [{1, 2}, {1, 2}] 2

[{2}, {1, 3}] [{1, 2}, {1, 2}] [{1, 2}, {1, 2}] 1

In Table 1, C collects condition attributes “Listening, Speaking, Reading, Writing”, and D has the decision

attribute “Excellent”. The intersection of the row and column represents the attribute value of the sample under the

corresponding attribute. For example, the ﬁrst unit [{C, S }, {E, C, S }] represents the attribute value of the sample x

under the conditional attribute “Listening”, and it has the interval-set form. Table 2 can be similarly analyzed.

In ISDSs, equivalence relations are not applicable, so the interval set similarity is proposed to construct similarity

classes and the similar granulation structure [24].

Deﬁnition 2 ([24]). Let A =

[

, A

]

and B =

[

, B

]

be two interval sets. The possible degree of A relative to B is

(A−B)

(

∩ B

), (1)

where | ∗ | denotes the cardinality of set ∗. The similarity degree between two interval sets is

S D

(AB)

[PD

(A−B)

+ PD

(B−A)

], (2)

where PD

(A−B)

and PD

(B−A)

are the possible degrees of A relative to B and B relative to A, respectively. Speciﬁcally

in ISDS, two samples x, y ∈ U regarding attribute c ∈ C concern two interval sets x = [x

−

, x

], y = [y

−

, y

], so their

similarity degree is

S D

(x, y) =

[PD

(x−y)

+ PD

(y−x)

]. (3)

Deﬁnition 3 (Similar granulation structure [24]). For IS DS = (U, C

D, V, f ) with a threshold δ ∈ [0, 1], the δ-

interval similarity relation about attribute c ∈ C is

S R

{

(x, y) ∈ U × U | S D

(x, y) ≥ δ

}

, (4)

and the corresponding similarity class of object x is S C

(x) = {y ∈ U | (x, y) ∈ S R

}. Regrading a non-empty attribute

subset B ⊆ C, the class of δ-interval similarity of sample x ∈ U is

S C

(x) = {y ∈ U | (x, y) ∈ S R

}, (5)

where S R

= {(x, y) ∈ U × U | ∧

c∈B

S D

(x, y) ≥ δ} means the similarity relation. All the similarity classes formulate

the similar granulation structure:

−−−→

S C

= (S C

), S C

), · · · , S C

)). (6)

Example 2. Considering ISDS in Table 2, we concern four attribute subsets on

B : {a

}, {a

, a

}, {a

, a

}, {a

, a

For δ = 0.5, similarity classes can be obtained, and relevant similar granulation structures become

−−−−→

S C

0.5

−−−−−−−→

S C

0.5

}

= ({x

}, {x

, x

}, {x

, x

}, {x

, x

}, {x

, x

}, {x

, x

}),

−−−−−−−→

S C

0.5

}

−−−−−−−−−→

S C

0.5

}

= ({x

}, {x

, x

}, {x

, x

}, {x

, x

}, {x

, x

}).

(7)

2.2. Basic three-view uncertainty measures with mixed conditional entropy

The conditional entropy and dependency degree serve as two fundamental uncertainty measures, and they rep-

resent the informational and algebraic perspectives, respectively. By reviewing and combining the two measures,

we here propose a mixed conditional entropy, and this integrated measure mainly follows the algebra-informational

perspective. Next, we discuss the three-view uncertainty measures, mainly based on the similar granulation structure

on ISDSs. In later studies, IS DS = (U, C

D, V, f ) with B ⊆ C and δ ∈ [0, 1] serves as a common context, and

∈ U/D represents the decision class in decision classiﬁcation U/D; moreover, the logarithmic function “log” is

related to bottom number 2.

剩余28页未读，继续阅读

评论收藏

内容反馈

谢大虾

粉丝: 42
资源: 5

在区间集决策系统中基于双粒化和三视角不确定性度量的系统性属性约简

最新资源