没有合适的资源?快使用搜索试试~ 我知道了~
“实数域中,负数没有平方根”,这是一个众所周知的重要结 论,由此可以得到两条简单推论:“实数域中,只有正数才能开偶次 方根”;“任意实数的偶次方根均大于等于零”。或许是为了让“数” 这个概念更加广泛,或许是为了让数与数之间的各种运算更加封闭, 又或许是为了研究某些问题的需要,二元数——复数——诞生了! 由实数单位“1”以及虚数单位“i”(−1的算术平方根)的所有线性 组合构成了整个复数域。本文主要就复数域为基础数学的发展所带 来的巨大便捷做一些简单的讨论。包括:运用复分析法证明求解一 些比较繁琐比较巧妙的平面几何问题、运用复变函数的柯西留数定 理求解一些难以计算的反常黎曼实积分、探究数学分析与复分析之 间的区别与联系等。
资源推荐
资源详情
资源评论

复分析及其应用
摘 要
“实数域中,负数没有平方根”,这是一个众所周知的重要结
论,由此可以得到两条简单推论:“实数域中,只有正数才能开偶次
方根”;“任意实数的偶次方根均大于等于零”。或许是为了让“数”
这个概念更加广泛,或许是为了让数与数之间的各种运算更加封闭,
又或许是为了研究某些问题的需要,二元数——复数——诞生了!
由实数单位“
1”以及虚数单位“ i ”( 1− 的算术平方根)的所有线性
组合构成了整个复数域。本文主要就复数域为基础数学的发展所带
来的巨大便捷做一些简单的讨论。包括:运用复分析法证明求解一
些比较繁琐比较巧妙的平面几何问题、运用复变函数的柯西留数定
理求解一些难以计算的反常黎曼实积分、探究数学分析与复分析之
间的区别与联系等。
关键词:复分析法,平面几何,柯西留数定理,反常积分,解析函
数,调和函数

Complex Analysis and Its Applications
Abstract
It is universally acknowledged that “Negative numbers do not have square roots in
the field of real numbers”. Thus we come to two simple deductions: “Only positive
numbers have even power roots in real number field” and “None of even power roots is
negative”. Probably in order to make the conception of “number” more extensive, the
operations more closed, or perhaps to meet the certain demands of the research, dyadic
numbers --- complex numbers --- got their start! The whole field of complex numbers
consists of all the linear combinations of the real number unit “
1” and the imaginary
number unit “
i ” (the arithmetic square root of 1− ). This thesis is mainly a brief
discussion of great benefits brought by the field of complex numbers to the development
of elementary mathematic, including using complex analysis method to prove or solve
some plane geometry problems that are complicated or ingenious, adopting Cauchy
Residue Theorem in complex analysis to figure out some improper Riemann integral in
real number field which is unquantifiable, exploring the difference and linking between
mathematical analysis and complex analysis, and so on.
Key words: Complex Analysis Method, Plane Geometry, Cauchy Residue Theorem,
Improper Integral, Analytical Function, Harmonic Function

目录
序言 从一个有趣的数学问题出发
曾祖父荒岛宝藏问题 ………………………………………………… 1
一、复分析在平面几何中的应用
1、化繁为简 …………………………………………………………… 4
2、化巧为简 …………………………………………………………… 7
二、复分析在计算实积分中的应用
1、计算积分路径上无奇点的反常黎曼积分 ………………………… 10
2、计算积分路径上有奇点的反常黎曼积分 ………………………… 14
三、数学分析与复分析的区别以及联系
1、数学分析与复分析的一些区别 …………………………………… 18
2、数学分析与复分析的简单联系 …………………………………… 21
总结
关于复分析应用的总结 ……………………………………………… 25
附录
附录一、参考文献 …………………………………………………… 26
附录二、声明 ………………………………………………………… 27

序言 从一个有趣的数学问题出发
第 1 页 共 27 页
序言 从一个有趣的数学问题出发
在实数域中,对于一个实系数一元二次方程
()
0 0
2
≠=++ acbxax , ,如果判别式
04
2
<−=Δ acb ,那么就会遇到负数开平方的问题,而在实数域中,负数没有平方根,因此,这
类方程就没有实根。例如:方程
01
2
=+x 。
16 世纪中叶,意大利数学家卡尔丹在 1545 年解三次方程时,把
40 看作 155 −+ 与 155 −−
的乘积,首次产生了对负数进行开平方运算的思想。然而,这只不过是一种纯粹形式上的表示而已,
当时,谁也说不清这种表示方法到底有什么样的好处。
关于复数理论最系统的叙述,是由著名的瑞士数学家欧拉在 1777 年作出的。他系统地建立了
复数理论,发现了复指数函数与三角函数之间的关系,并创立了复变函数论的一些基本定理。用符
号
i 作为虚数的单位也是欧拉首创的。此后,复数理论才被人们承认及使用。
19 世纪,复变函数的理论经过法国数学家柯西、德国数学家黎曼和魏尔斯特拉斯的巨大努力,
已经形成了非常系统的理论,并且深刻地渗透到代数学、解析数论、微分方程、概率统计、计算数
学和拓扑学等数学分支。同时,复变函数论在热力学、流体力学和电学等方面也有很多的应用。
20 世纪以来,复变函数已被广泛的应用于理论物理、弹性理论和天体力学等方面,与数学中其
他分支的联系也日益紧密。另外,在种种抽象空间的理论中,复变函数还常常为人们提供新思想与
新模型。
曾祖父荒岛宝藏问题
从前,有一个富有冒险精神的年轻人,在他曾祖父的遗物中发现了一张羊皮纸。上面
指明了一处宝藏。它是这样写着的:
乘船至北纬××西经××,即可找到一座荒岛。岛的北岸有一大片草地,草地上有一
颗橡树和一颗松树,还有一座绞架,那是过去用来吊死叛变者的。从绞架走到橡树,并记
住走了多少步;到了橡树,向右拐个直角再走那么多步,在那里打个桩。然后回到绞架那
里,朝松树走,同时记住所走的步数;到了松树,向左拐个直角再走这么多步数。在那里
序言 从一个有趣的数学问题出发
第 2 页 共 27 页
也打个桩。两个桩的正中就是宝藏所埋藏的地点。
于是,这个年轻人顺着羊皮纸上所留下的信息,找到了这座荒岛,也找到了羊皮纸上
所写的橡树和松树,但绞架却不见了,可能是经过了多年的风吹日晒雨淋,已化为尘土。
年轻人便不甘心地在地上狂乱地挖了起来,但最终由于地方太大,他只好两手空空地失望
而归。
这是一个令人伤心的故事,然而,更加令人伤心的是,如果这个年轻人能够懂得一些数学知识,
尤其是关于复数部分的理论,那么他是可以很顺利地找到宝藏的。让我们来帮助这位年轻人找出宝
藏吧!
把这座荒岛看成整个复平面,以两树连线段的中点为坐标原点,以两树的连线段所在的直线为
实轴,以经过两树连线段的中点并且垂直于实轴的直线为虚轴,并且以两树间距离的一半作为单位
长度,建立复平面直角坐标系,将原问题转化成为复分析问题。
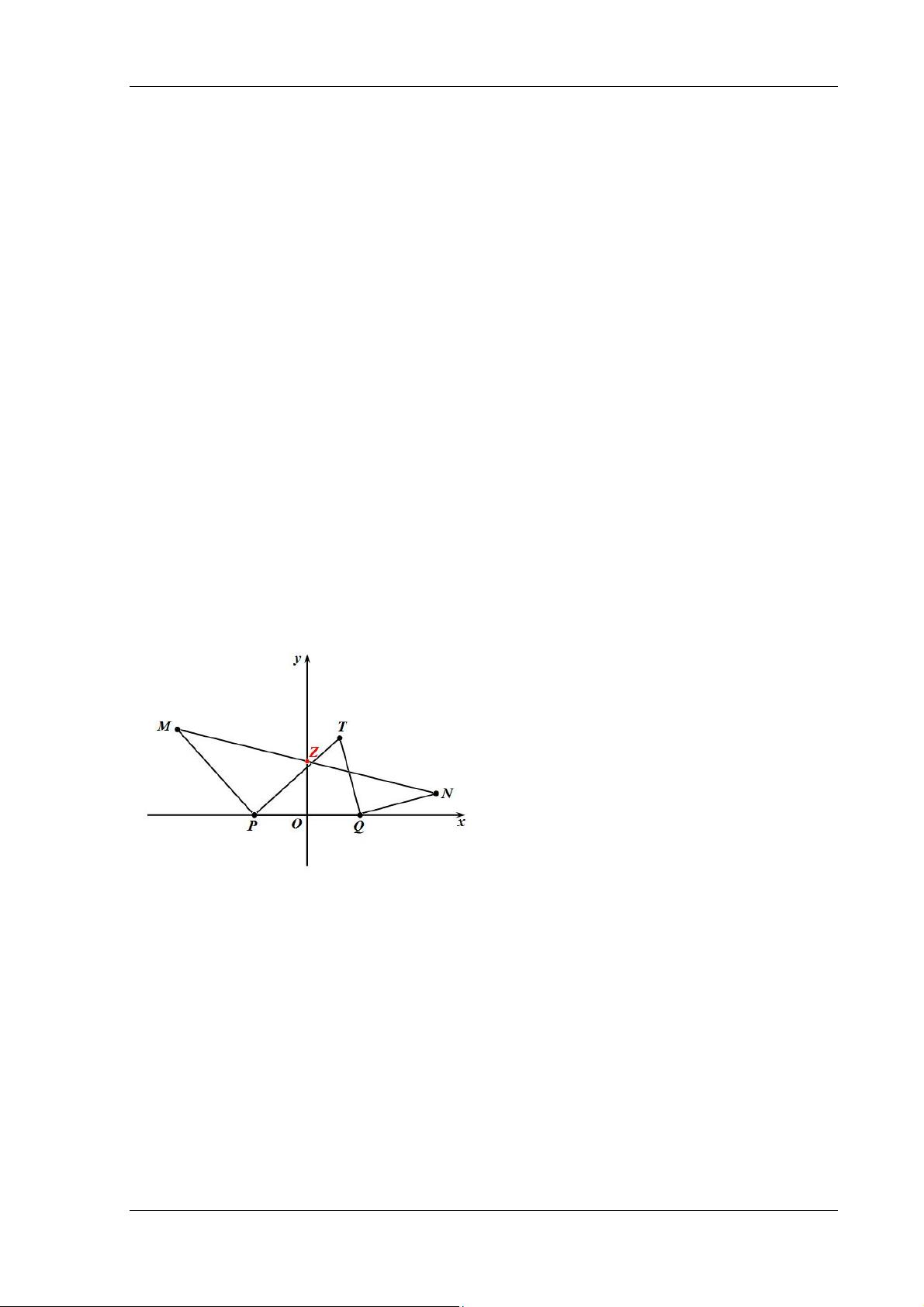
如图,在复平面直角坐标系
xOy 中,已知 P 、 Q 两点的坐标分别为
()
0,1−P 、
()
0,1Q ,
T
为平面
上任意一点,分别连接
T
P
、TQ ,将线段 P
T
绕点
P
逆时针旋转
0
90 到 PM ,将线段 QT 绕
点
Q 顺时针旋转
0
90 到 QN ,连 接 MN ,
Z
是
MN 的中点
求:
Z
的坐标
解:
znmtqpoZNMTQPO 、、、、、、所对应的复数分别为、、、、、、设点
110 =−== qpo ,,则
()
Ryxbayixzbiat ∈+=+= 、、、,,令
biaqt
biapt
+−=−
++=−∴
1
1
()( ) ()
()( ) ()
iabbiaiqtiqn
iabbiaiptipm
11
11
−−=+−−=−−=−
++−=++=−=−∴
剩余29页未读,继续阅读
资源评论

一只Monet
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功