西工大计算机实习报告.doc

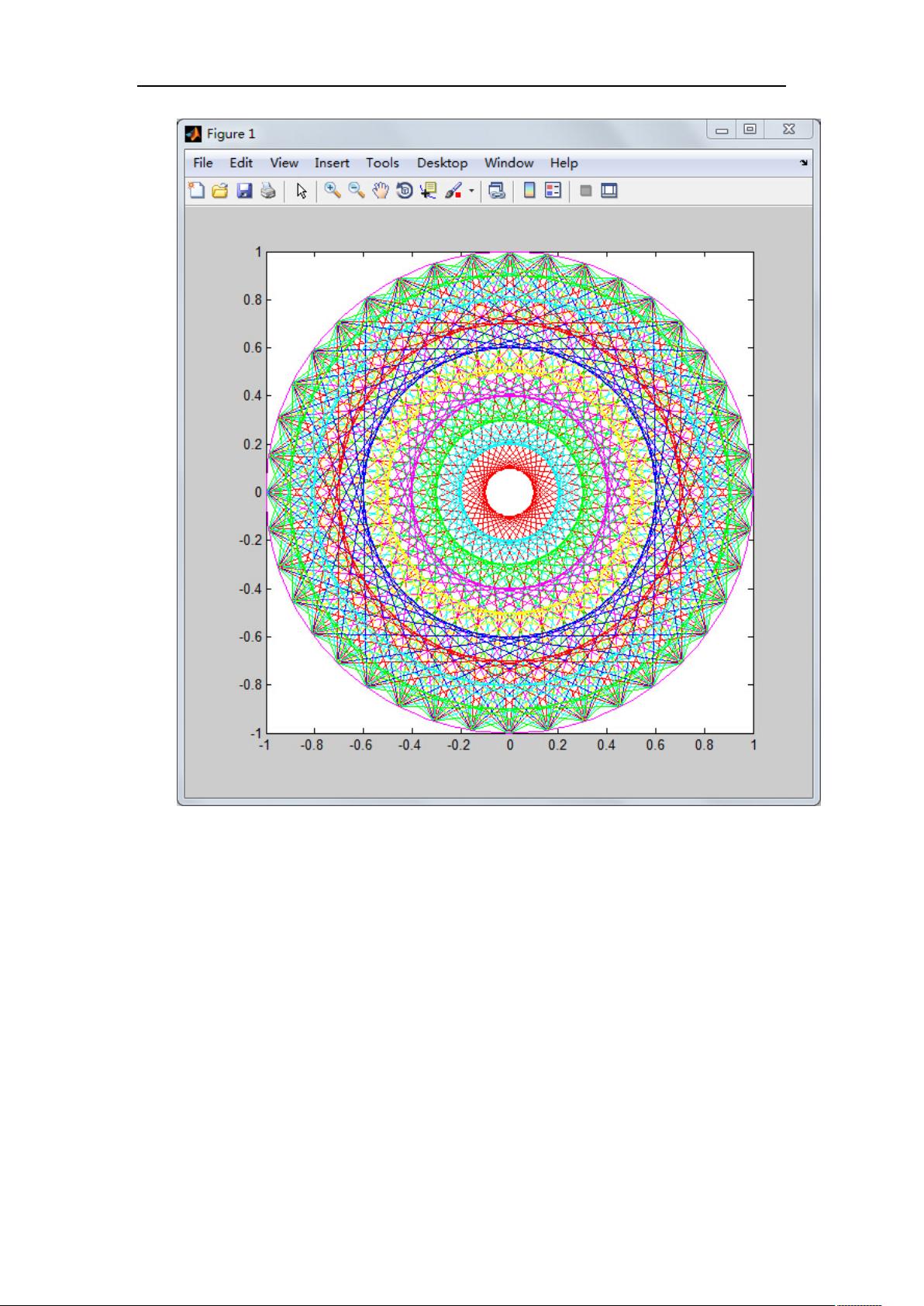
计算机实习报告 趣味题 彩色的圆环： 分析图形可知，一共有n个同心圆，外面大圆n等分，然后从每个等分点作所有同心圆的 两条切线。如果用极坐标表示，可以很容易求解切点，代码如下所示： n=10; %同心圆数量 m=40; %等分点数 R=1; %外圆半径 s=0:0.01*pi:2*pi; %控制圆的光滑程度的极坐标角度 t=0:2*pi/m:2*pi; %等分点极坐标角度 x0=R*cos(t);y0=R*sin(t); %等分点直角坐标 color=['b','r','c','g','m','y']; %画图颜色 lc=length(color); %颜色数量长度,超出后从头开始 for i=1:n %开始同心圆循环 r=R/n*i; %当前同心圆半径 a=acos(r/R); %切线与圆心线角度（弧度制） x1=r*cos(t-a);y1=r*sin(t-a); %任意等分点相对当前同心圆的第一个切点 x2=r*cos(t+a);y2=r*sin(t+a); %任意等分点相对当前同心圆的第二个切点 plot(r*cos(s),r*sin(s),color(mod(i,lc)+1)) 【西工大计算机实习报告】涉及的知识点主要包含两部分：趣味题——彩色的圆环绘制，以及算法题——求无向图的最短路径（Dijkstra算法）。 让我们详细探讨彩色圆环的绘制过程。这个趣味题是通过编程实现一个图形，涉及到的主要编程语言是MATLAB。在MATLAB中，我们可以通过极坐标来描述和绘制圆环。具体步骤如下： 1. 定义同心圆的数量（n）、等分点数（m）以及外圆的半径（R）。 2. 使用极坐标角度s和t来控制圆的平滑度和等分点位置。 3. 为不同颜色的线条定义数组color，并计算颜色数量长度lc，以便循环使用颜色。 4. 对于每个同心圆（i从1到n），计算其半径r，并求得切线与圆心线的角度a。 5. 根据角度a，计算等分点相对于当前同心圆的两个切点坐标（x1, y1和x2, y2）。 6. 使用plot函数绘制同心圆和切线，使用hold on命令保持当前图像，使得多个图形在同一轴上绘制。 7. 设置坐标轴的比例一致（axis equal），确保图形的视觉效果。 接下来，我们转向算法部分，这里讨论的是Dijkstra算法，一种用于寻找图中两点间最短路径的算法。Dijkstra算法适用于解决带权无向图的问题，但在实习报告中，作者扩展了它的应用，包括处理有向图和有向带权图。 Dijkstra算法的基本思想如下： 1. 初始化：设置所有顶点的距离为无穷大（除了起始点设为0），并创建一个优先队列（如最小堆）存储未访问的顶点。 2. 进行迭代：在每个步骤中，找到距离源点最近的顶点（即优先队列中的最小元素），将其标记为已访问，并更新与之相邻且未访问过的顶点的距离。 3. 重复步骤2，直到队列为空或目标顶点被访问。 4. 结果：最终得到的各个顶点距离表示从源点到每个顶点的最短路径长度。 在C++实现中，通常会使用邻接矩阵或邻接表来存储图的信息，同时使用数据结构如队列或堆来辅助算法执行。报告中提到的类`tu`可能就是用来表示图的数据结构，其中包含顶点、弧边、矩阵等成员变量，以及增加顶点、弧边、遍历图、求最短路径等相关操作的成员函数。 这份实习报告涵盖了图形绘制的MATLAB编程技巧和图论中的经典算法——Dijkstra算法，对于学习计算机图形学和图算法的学生来说具有很高的参考价值。通过实际操作和编程，实习生可以深入理解这些理论知识在实际问题中的应用。