【数据结构】数据结构-图的基本概念.pdf

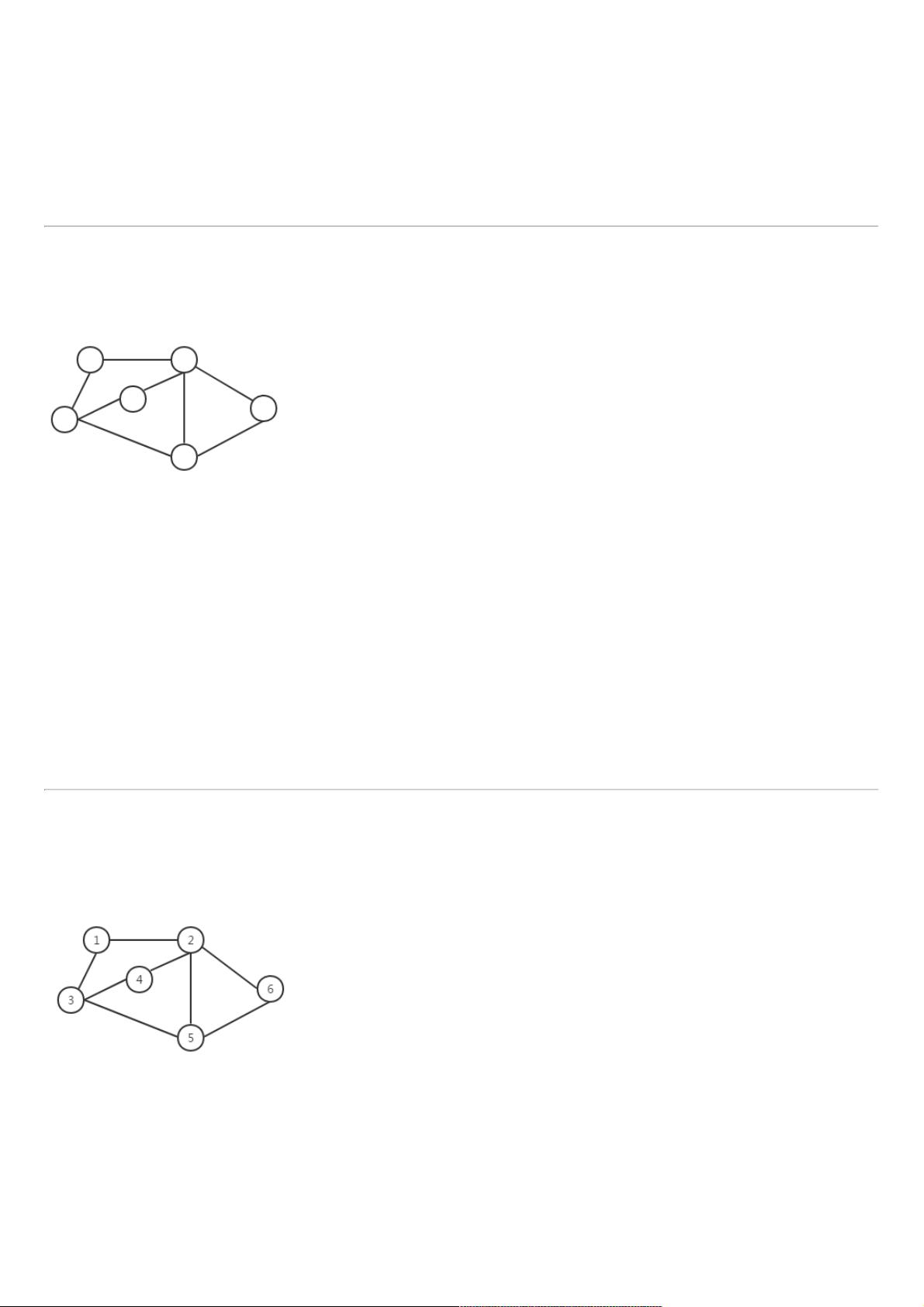
【数据结构】数据结构 【数据结构】数据结构-图的基本概念 图的基本概念 图的简介 图（Graph）结构是⼀种⾮线性的数据结构，图在实际⽣活中有很多例⼦，⽐如交通运输⽹，地铁⽹络，社交⽹络，计算机中的状态执⾏ （⾃动机）等等都可以抽象成图结构。图结构⽐树结构复杂的⾮线性结构。 图结构构成 1.顶点（vertex）：图中的数据元素，如图⼀。 2.边（edge）：图中连接这些顶点的线，如图⼀。 图⼀ 所有的顶点构成⼀个顶点集合，所有的边构成边的集合，⼀个完整的图结构就是由顶点集合和边集合组成。图结构在数学上记为以下形 式： G=（V,E） 或者 G=（V（G），E（G）） 其中 V（G）表⽰图结构所有顶点的集合，顶点可以⽤不同的数字或者字母来表⽰。E（G）是图结构中所有边的集合，每条边由所连接 的两个顶点来表⽰。 图结构中顶点集合V（G）不能为空，必须包含⼀个顶点，⽽图结构边集合可以为空，表⽰没有边。 图的基本概念 1.⽆向图（undirected graph） 如果⼀个图结构中，所有的边都没有⽅向性，那么这种图便称为⽆向图。典型的⽆向图，如图⼆所⽰。由于⽆向图中的边没有⽅向性， 这样我们在 数据结构中的图是一种非常重要的非线性数据结构，它广泛应用于现实生活中的许多场景，比如交通网络、社交网络以及计算机的状态执行等。图是由顶点（vertex）和边（edge）组成的，其中顶点代表数据元素，而边则表示顶点间的关系。 在数学上，一个图可以用G=(V,E)的形式表示，这里的V(G)表示所有顶点的集合，E(G)表示所有边的集合。每个顶点可以用不同的符号标识，每条边则由它连接的两个顶点来定义。图的顶点集合不能为空，至少要有一个顶点，但边集合可以为空，意味着图中可能不存在任何边。 图的基本类型主要包括： 1. **无向图（Undirected Graph）**：无向图中的边没有方向性，因此边的两端顶点是等价的。例如，在图二所示的无向图中，顶点V2与V5之间的边，既可以表示为(V2, V5)，也可以表示为(V5, V2)。无向图的邻接顶点是相互关联的。 2. **有向图（Directed Graph）**：有向图的边具有方向性，边的方向从一个顶点指向另一个顶点。例如，<V2, V6>表示一条从V2指向V6的边。有向图中，顶点的度分为入度（ID(V)）和出度（OD(V)），分别表示以该顶点为终点的入边数和起点的出边数。总度是入度与出度之和。 3. **混合图（Mixed Graph）**：混合图同时包含有向边和无向边，这种图结构在现实生活中更为常见，例如交通网络中的单行道和双行道。 4. **顶点的度（Degree of Vertex）**：度是与一个顶点相连的边的数量。在无向图中，顶点V的度D(V)等于与其相邻的边数。而在有向图中，顶点的总度是其入度和出度之和。 5. **邻接顶点（Adjacent Vertices）**：邻接顶点是指共享同一边的两个顶点。在无向图中，任何两个通过边连接的顶点都是邻接顶点。在有向图中，邻接顶点分为入边邻接顶点和出边邻接顶点，分别对应边的起点和终点。 6. **无向完全图（Undirected Complete Graph）**：在无向完全图中，任意两个不同的顶点之间都有一条边。如图四所示，每个顶点与其他所有顶点都有边相连。 了解这些基本概念对于理解和操作图结构至关重要，它们为解决诸如最短路径、遍历、连通性等问题提供了基础。在算法设计中，图论的方法经常被用来解决复杂的问题，例如Dijkstra算法用于找到图中两点间的最短路径，而深度优先搜索（DFS）和广度优先搜索（BFS）则是遍历图的常用方法。