电力系统分析第三章新.pptx

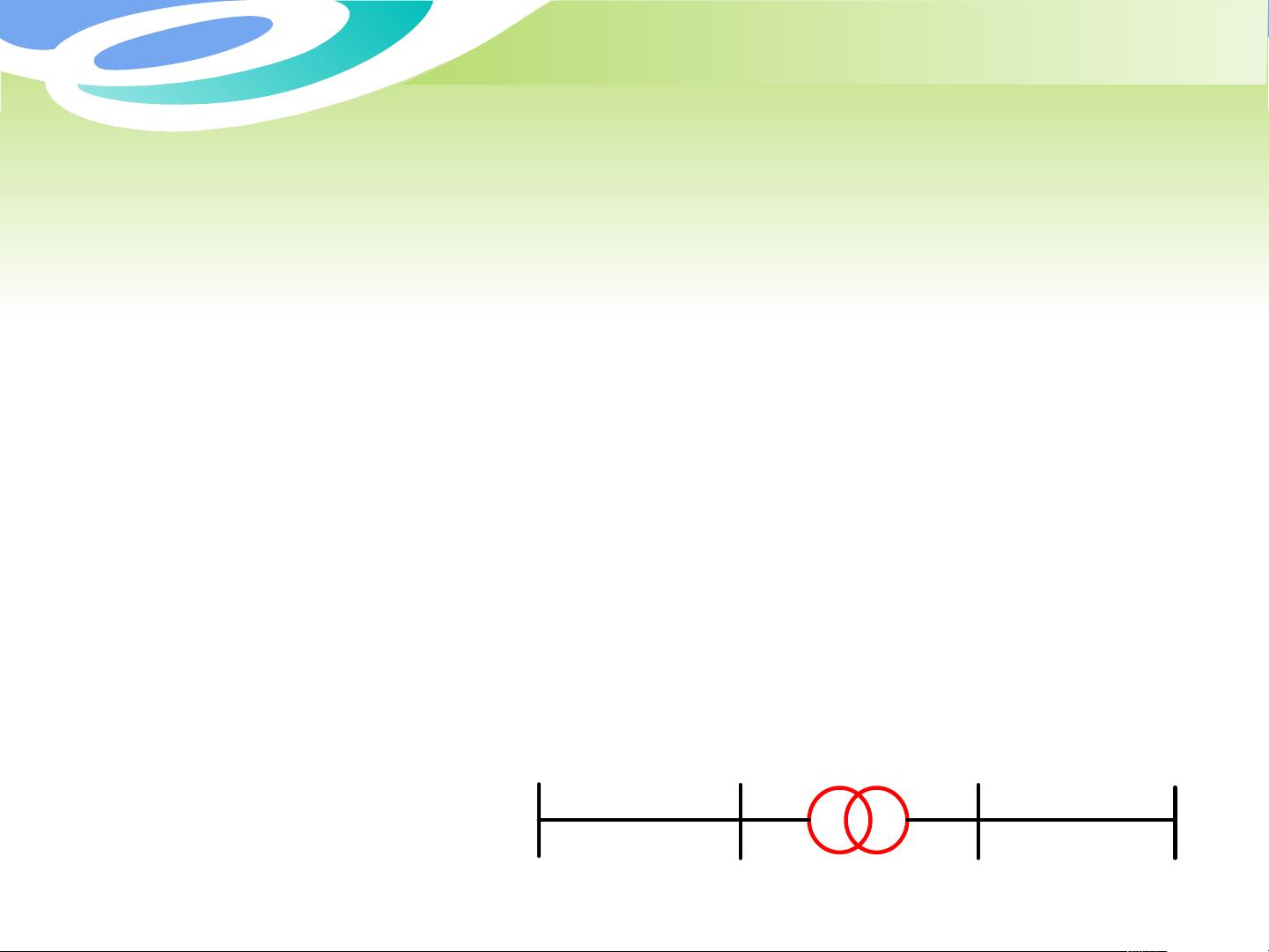
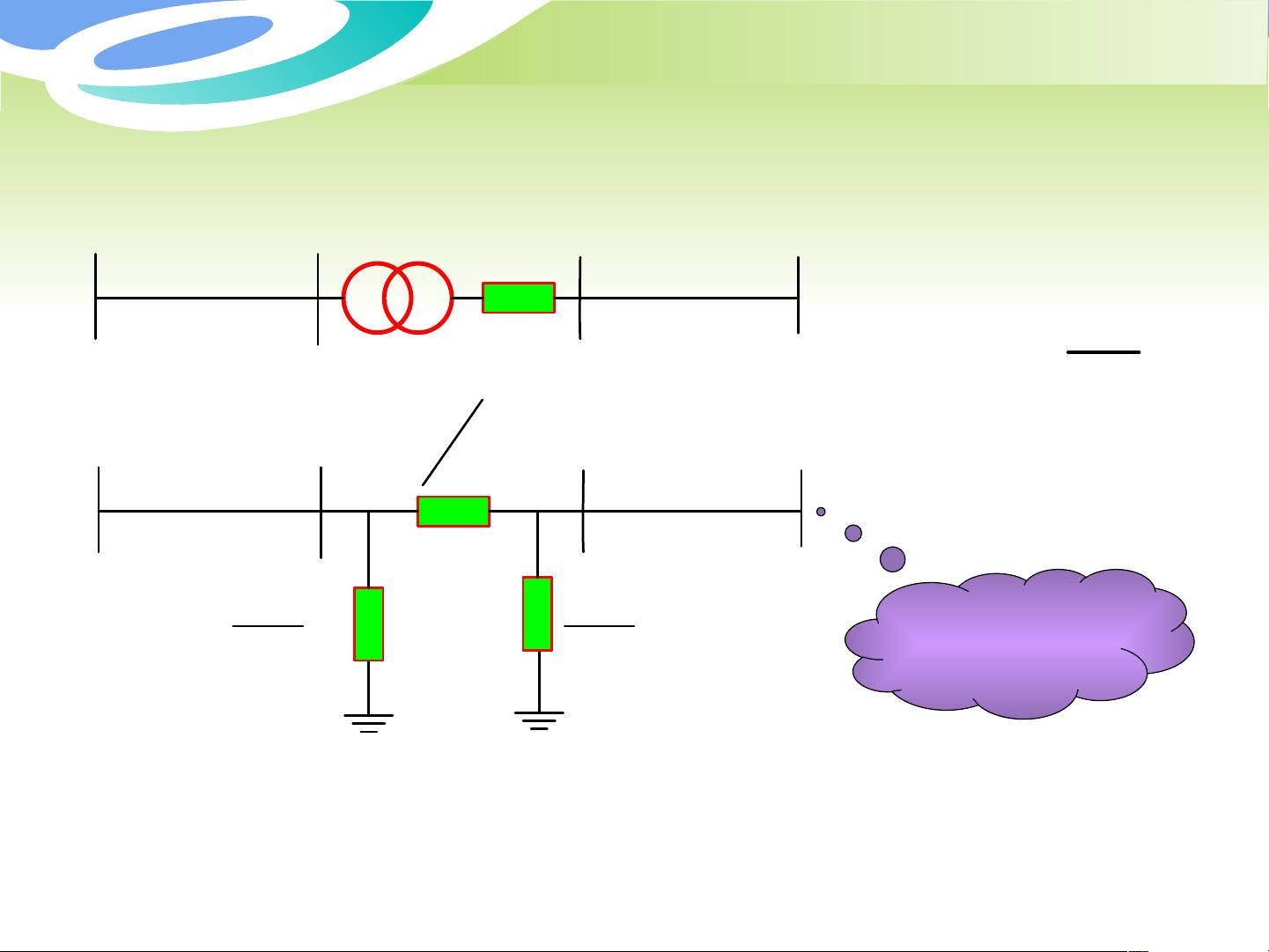
电力系统分析是电力工程中的核心课程，主要研究电力系统稳态运行时的电压、电流分布以及功率流动等问题。本章重点介绍了电力系统潮流的计算机算法，这是解决电力系统实际问题的关键技术之一。潮流计算旨在求解电力网络中各节点电压和支路电流的数值解，以确保系统的稳定运行。 电力网络的数学模型是建立在一系列假设之上的，包括所有参数用标幺值表示，简化线路和变压器为π型等值电路，以及将负荷模型化为恒功率或恒阻抗模型等。其中，π型等值电路由两段串联的阻抗（L-I和L-II）代表线路，用于描述线路的电气特性。对于双绕组变压器，可以等效为变比为k的理想变压器加上自身的阻抗ZT，这样就无需再按变比进行参数归算。 节点功率是电力系统分析的基础概念，它是由电源注入的功率和负荷抽取的功率的代数和。在节点电压方程的表示形式中，利用节点导纳矩阵Y和节点阻抗矩阵Z来描述网络中节点间的相互关系。Y矩阵的元素Yii代表节点i的自导纳，Yij代表节点i和j之间的互导纳，而Z矩阵则是Y的逆矩阵，其元素Zii表示节点i的自阻抗，Zij为节点i和j的互阻抗。这些矩阵的元素定义了在网络中注入单位电流或电压时，其他节点的响应。 节点电压方程的数学表达式为I = YU，这表明节点注入电流是节点电压与节点导纳矩阵的乘积。同样，节点电流方程为U = ZI，即节点电压等于节点阻抗矩阵与节点注入电流的乘积。通过这些方程，我们可以求解出网络中各个节点的电压和电流。 节点导纳矩阵Y和阻抗矩阵Z的特点在于它们反映了网络结构和元件特性。自导纳和自阻抗描述了节点自身的电气特性，而互导纳和互阻抗则反映了节点间的影响。例如，当节点i施加单位电压，其余节点接地时，互导纳Yij给出了节点j注入网络的电流；相反，当节点i注入单位电流，互阻抗Zij则表示节点j的电压。 在实际计算中，电力系统潮流的计算机算法通常采用牛顿-拉夫森迭代法或快速分解法等方法，通过不断迭代逼近非线性潮流方程的解。这些算法的目的是在考虑到电网的实际约束（如发电机和线路的功率极限）下，找出使得功率供需平衡且电压、电流满足规定的稳定状态。 电力网络的数学模型和潮流计算的计算机算法是理解和分析电力系统运行状态的基础工具。通过这些理论和方法，工程师能够预测和优化电力系统的运行，确保其高效、安全地供电。在实际应用中，这些知识对于电力系统的规划、设计、运行和控制都至关重要。