
Bar-Ilan University
Dept. of Computer Science
Shai Halevi – IBM Research
Based Mostly on [van-Dijk, Gentry, Halevi,
Vaikuntanathan, EC 2010]
1
Winter School on Secure Computation and Efficiency
Bar-Ilan University, Israel 30/1/2011-1/2/2011

Bar-Ilan University
Dept. of Computer Science
Secure Computation and Efficiency
Bar-Ilan University, Israel 2011
Part I
2

Bar-Ilan University
Dept. of Computer Science
Storing an encrypted file F on a remote server
Later send keyword w to server, get answer,
determine whether F
contains w
◦ Trivially: server returns the entire encrypted file
◦ We want: answer length independent of |F|
Claim: to do this, sufficient to evaluate
low-degree polynomials on encrypted data
◦ degree ~ security parameter
3
Secure Computation and Efficiency
Bar-Ilan University, Israel 2011

Bar-Ilan University
Dept. of Computer Science
File is encrypted bit by bit, E(F
1
) E(F
2
) … E(F
t
)
Word has s bits w
1
w
2
…w
s
For i=1,2,…,t-s+1, server computes the bit
c
i
=
◦ c
i
=1 if w appears at position i, else c
i
=0
◦ Each c
i
is a degree-s polynomial in the F
i
‟s
Trick from [Smolansky‟93] to get degree-n polynomials,
error-probability 2
-n
Return n random subset-sums
of the c
i
‟s (mod 2) to client
◦ Still degree-n, another 2
-n
error
4
2 mod )1(
1
1
s
j
jij
Fw
Secure Computation and Efficiency
Bar-Ilan University, Israel 2011
Bar-Ilan University
Dept. of Computer Science
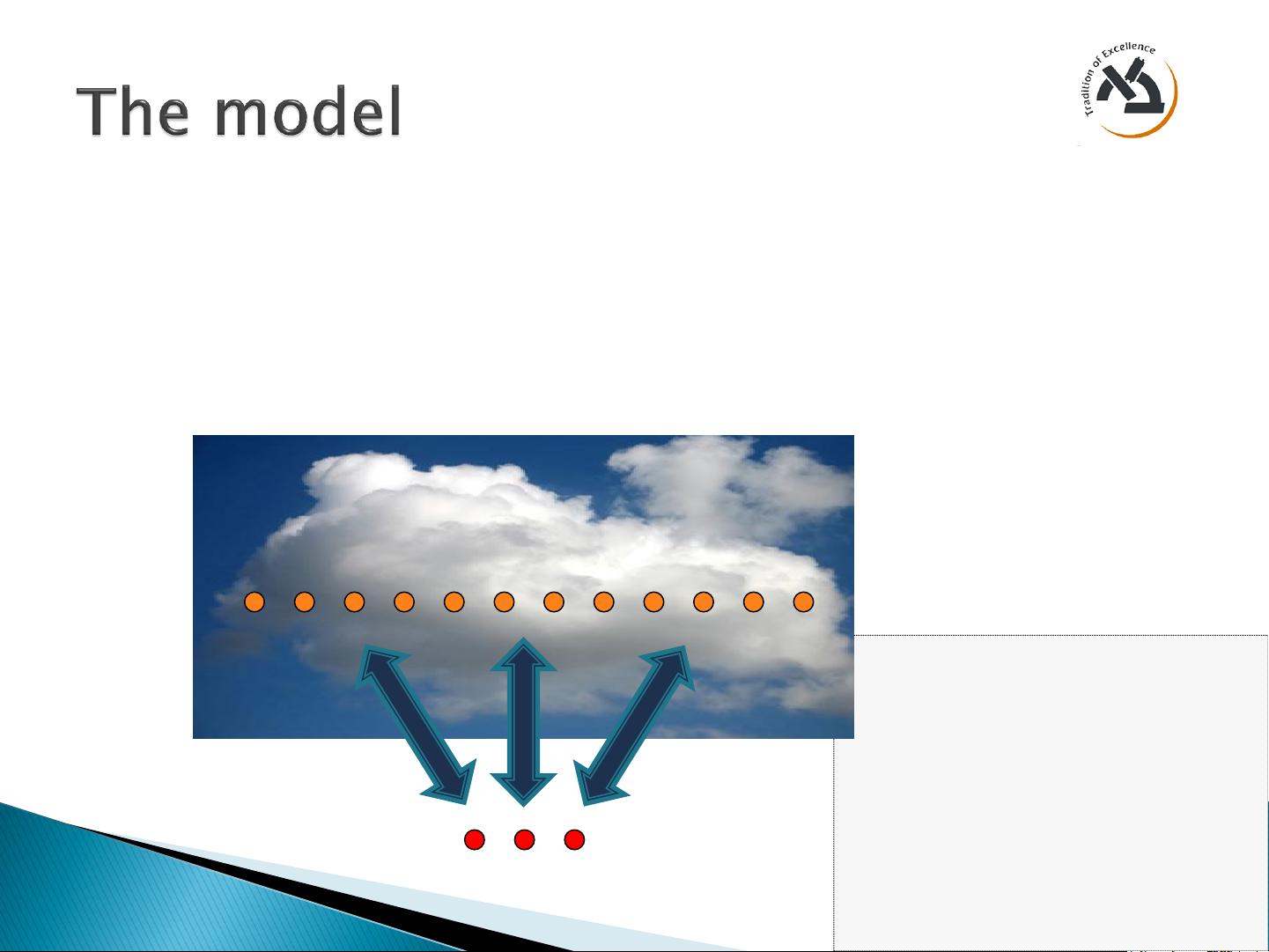
Want an encryption scheme (Gen, Enc, Dec)
◦ Say, symmetric bit-by-bit encryption
◦ Semantically secure, E(0)E(1)
Another procedure: Eval(f, C
1
,…C
t
)
◦ f is a binary polynomial in t variables, degreen
Represented as arithmetic circuit
◦ The C
i
‟s are ciphertexts
For any such f, and any C
i
=Enc(x
i
) it holds that
Dec( Eval(f, C
1
,…C
t
) ) = f(x
1
,…,x
t
)
◦ Also |Eval(f,…)| does not depend
on the “size” of f (i.e., # of vars
or # of monomials, circuit-size)
◦ That‟s called “compactness”
5
Secure Computation and Efficiency
Bar-Ilan University, Israel 2011
















