
http://jrp.sagepub.com
Composites
Journal of Reinforced Plastics and
DOI: 10.1177/0731684407079753
2007; 26; 1135 Journal of Reinforced Plastics and Composites
Zheng-Ming Huang
with a General Constitutive Relationship
Inelastic and Failure Analysis of Laminate Structures by ABAQUS Incorporated
http://jrp.sagepub.com/cgi/content/abstract/26/11/1135
The online version of this article can be found at:
Published by:
http://www.sagepublications.com
can be found at:Journal of Reinforced Plastics and Composites Additional services and information for
http://jrp.sagepub.com/cgi/alerts Email Alerts:
http://jrp.sagepub.com/subscriptions Subscriptions:
http://www.sagepub.com/journalsReprints.navReprints:
http://www.sagepub.co.uk/journalsPermissions.navPermissions:
http://jrp.sagepub.com/cgi/content/refs/26/11/1135 Citations
at ZHEJIANG UNIV LIB on May 23, 2009 http://jrp.sagepub.comDownloaded from

Inelastic and Failure Analysis of Laminate
Structures by ABAQUS Incorporated with
a General Constitutive Relationship
ZHENG-MING HUANG*
School of Aerospace Engineering and Applied Mechanics
Tongji University, 1239 Siping Road
Shanghai 200092, PR China
ABSTRACT: A general constitutive relationship for describing the inelastic and strength behavior
of laminated composites reinforced with various fiber preforms was presented in References [1,2].
The relationship is consistent in that when the fiber disappears or becomes the same as the matrix,
the nonlinear constitutive equations of the resulting composite deteriorate to those of the isotropic
matrix material. One of the best benefits of the constitutive relationship is that all the formulas
involved are in explicit form and only the properties of the constituent fiber and matrix of the
composite are required as input material data. This will significantly simplify a finite element
analysis for a laminated structure. In the present paper, the general constitutive relationship for tape
laminates was programmed into a user subroutine, UGENS, of the commercial finite element (FE)
software ABAQUS. Several laminated structures including a complicated bone plate were then
analyzed, and good correlation between the numerical results and available experimental data was
found. A list of the original computer code together with an input data file was summarized in the
appendixes of the paper.
KEY WORDS: laminated composite, composite structure, nonlinear behavior, ultimate strength,
FEM analysis, ABAQUS, user subroutine, computer code.
INTRODUCTION
A
S A STRUCTURAL material, fiber reinforced composite laminates are increasingly used
in aerospace and many other engineering fields due to high stiffness and strength to
weight ratios as well as capability in tailoring mechanical performance. In these
applications, it is necessary to assess the load carrying capacity and structural integrity
of the composite structures. It is well known that before the laminate attains its ultimate
strength, a progressive failure process takes place and some laminas in the laminate
generally have undergone inelastic deformation. Because each lamina is a statically
indeterminate element in the laminate, an accurate determination of the lamina load share
and hence the overall load carrying capacity of the laminate requires the use of a nonlinear
constitutive relationship for the composite.
*Author to whom correspondence should be addressed. E-mail: huangzm@mail.tongji.edu.cn
Figure 12 appears in color in color online: http://jrp.sagepub.com
Journal of REINFORCED PLASTICS AND COMPOSITES, Vol. 26, No. 11/2007 1135
0731-6844/07/11 1135–47 $10.00/0 DOI: 10.1177/0731684407079753
ß SAGE Publications 2007
Los Angeles, London, New Delhi and Singapore
at ZHEJIANG UNIV LIB on May 23, 2009 http://jrp.sagepub.comDownloaded from

Unfortunately, the nonlinear mechanical behavior of a composite is not well understood
in the current literature. Recently, the present author proposed a general constitutive
theory, the bridging model [3,4], for composites. By combining the bridging model with the
classical lamination theory, a general constitutive relationship was established for any
fibrous laminate, and was summarized in References [1,2]. A recently completed
worldwide failure exercise [5–8] has indicated that the bridging model constitutive
theory had two unique features. The first feature was that it was the only model in the
exercise that could be used to calculate the thermal stresses in the fiber and matrix
materials due to a thermal load (temperature variation) applied on the composite
(see Reference [6], p. 450). The second feature lay in the fact that the model is consistent
in that the laminate nonlinear constitutive equations automatically deteriorate to those
of the isotropic matrix material when the fiber content becomes zero or when the
fiber becomes the same as that of the matrix. It is noted that, the other nonlinear
constitutive models used in the exercise [9–15] described the composite
constitutive equations in a way somewhat similar to Hooke’s law. Namely, a shear
stress would not cause an extensional strain whereas a normal stress had no contribution
to a shear strain. According to a classical plasticity theory such as Prandtl–Reuss
theory for isotropic materials, however, a normal (or shear) stress will generate a shear
(or extensional) plastic strain if the material is subjected to a combination of the shear
and normal stresses.
The finite element method has been realized to be one of the most powerful tools in
improving design quality and reducing development time for engineering structures.
Several well-known commercial finite element codes, such as ABAQUS, are capable
of analyzing the nonlinear response and strength behavior of a very complicated structure.
However, their applicability to the structures made of laminated composites is restricted,
due to a shortage of an efficient inelastic constitutive module for composites in the
material libraries of those codes. The purpose of this paper is to incorporate the
bridging model based nonlinear constitutive relationship for mul tidirectional tape
laminates into ABAQUS through programming a user subroutine UGENS, as though a
new module is added into the ABAQUS material library. In this way, any structure with
tape laminates involved, either a sole laminated structure or a structure consisting
of laminates and other materials for which constitutive modules are provided in the
ABAQUS library, which is subjected to arbitrary load condition can be FE analyzed
readily. In the following sections, the routine development, original subroutine code,
instructions for providing input data, and an illustration example are pr esente d.
The original computer code and an input data file are provided in Appendices A and B
of the paper.
SUMMARY OF CONSTITUTIVE RELATIONS
For convenience of expression, necessary equations are summarized below. More details
can refer to References [1–4]. Within the scope of the classical laminate theory, the nonzero
stress and strain increments, fdg
L
k
and fd"g
L
k
, of the kth lamina of a laminate in the
laminate coordinate system (Figure 1) are given by
fdg
L
k
¼ð½T
c
Þ
k
ð½S
k
Þ
1
ð½T
T
c
Þfd"g
L
k
fg
L
k
dT
¼½ðC
L
ij
Þ
k
fd"g
L
k
fg
L
k
dT,
ð1Þ
1136
Z.-M. HUANG
at ZHEJIANG UNIV LIB on May 23, 2009 http://jrp.sagepub.comDownloaded from
where
fd"g
L
k
¼ d"
0
xx
þ
z
k
þ z
k1
2
d
0
xx
,d"
0
yy
þ
z
k
þ z
k1
2
d
0
yy
,2d"
0
xy
þðz
k
þ z
k1
Þ d
0
xy
no
T
, ð2:1Þ
and
fg
L
k
¼fð
1
Þ
L
k
, ð
2
Þ
L
k
, ð
3
Þ
L
k
g
T
¼ð½T
c
Þ
k
ð½S
k
Þ
1
fg
k
: ð2:2Þ
d"
0
xx
,d"
0
yy
, and d"
0
xy
and d
0
xx
,d
0
yy
, and d
0
xy
are the laminate in-plane strain and curvature
increments. ‘‘L’’ refers to the laminate coordinate system shown in Figure 1. z
k
and z
k1
are the z coordinates of the top and the bottom surfaces of the kth lamina in the laminate
system. [T]
c
is a coordinate transformation matrix between the laminate coordinate
system and the material principal coordinate system of the lamina, i.e., (x
1
, x
2
)in
Figure 2(b). dT is a temperature increment sustained by the laminate. By the Bridging
Model, the current compliance matrix and thermal expansion coefficient of the lamina
in the material principal coordinate system are derived as [3].
½S¼ðV
f
½S
f
þV
m
½S
m
½AÞ½Bð3Þ
fg¼V
f
f
f
gþV
m
f
m
gþV
m
ð½S
m
½S
f
Þfb
m
gð4Þ
θ=θ
1
<0
θ=θ
2
=0
θ=θ
3
>0
x
1
x
1
x
y
z
dσ
11
dσ
11
dσ
22
dσ
12
x
2
x
1
dσ
xx
dσ
xx
dσ
xy
dσ
yy
x
1
x
2
x
y
(
c
)(
b
)(
a
)
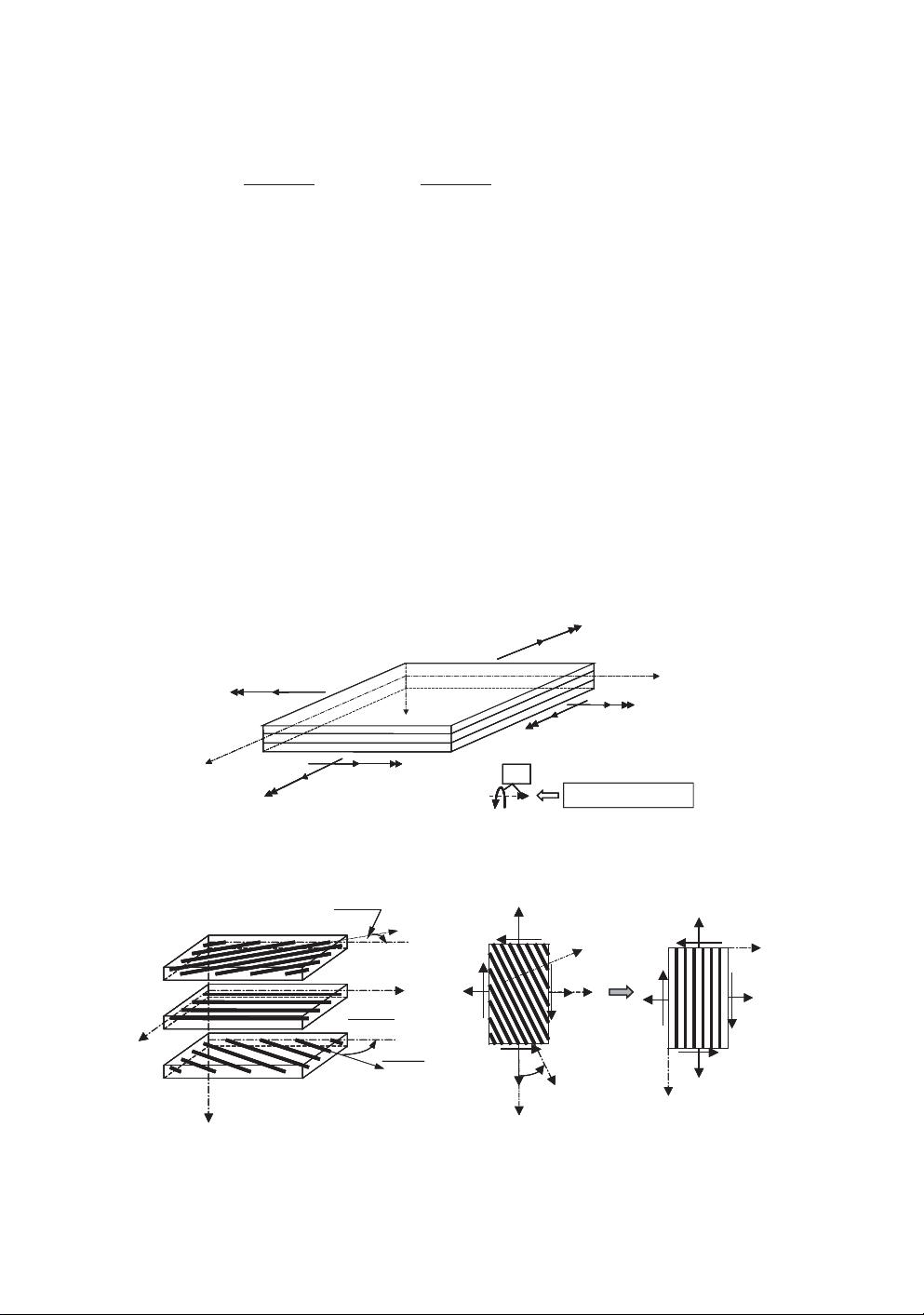
Figure 2. (a) Laminate system with ply-angle, (b) lamina in laminate system, (c) lamina in material principal
coordinate system.
dM
yx
dM
yy
dN
yy
dM
xx
dM
xy
dN
xx
dN
yx
dN
xy
dM
x
y
z
zz
z
Vector of a moment
Figure 1. Laminate coordinate system together with applied force and moment increments.
Analysis of Laminate Structures by ABAQUS 1137
at ZHEJIANG UNIV LIB on May 23, 2009 http://jrp.sagepub.comDownloaded from

where [B] ¼ (V
f
[I] þ V
m
[A])
1
, V
f
and V
m
denote the volume fractions of the fiber and
matrix materials, [S
f
] and [S
m
] are the current compliance matrices of the fiber and matrix
materials, {
f
} and {
m
} are the current thermal expansion coefficients of the fiber and
matrix materials respectively, and [I] is a unit matrix.
Internal stress increments in the matrix and fiber are correlated with the stress
increments applied to the lamina, {d } ¼ {d
11
,d
22
,d
12
}
T
, in the material principal
coordinates via:
fd
f
g¼½Bfdgþfb
f
g dT, ð5:1Þ
fd
m
g¼½A½Bfdgþfb
m
g dT, ð5:2Þ
V
f
fb
f
gþV
m
fb
m
g¼f0g, ð5:3Þ
fb
m
g¼ð½I½A½BÞð½S
f
½S
m
Þ
1
ðf
m
gf
f
gÞ, ð5:4Þ
where the stress increments in the lamina principal system are obtained from the ones in
the laminate system, given by Equation (1), through a coordinate transformation
fdg
k
¼ð½T
T
s
Þ
k
fdg
L
k
, ð6Þ
[T]
s
is another coordinate transformation matrix different from [T]
c
. The bridging matrix
[A] together with [B] are expressed as:
½A¼
a
11
a
12
a
16
0 a
22
a
26
00a
66
2
6
6
4
3
7
7
5
and ½B¼
b
11
b
12
b
16
0 b
22
b
26
00b
66
2
6
6
4
3
7
7
5
ð7Þ
Explicit expressions of a
ij
and b
ij
can be found in, e.g., Reference [3].
FAILURE CRITERIA
The total stresses in the fiber and matrix materials as well as on the lamina are updated
in the following way
f
m
g
k
¼f
m
g
k
þfd
m
g
k
, ð8:1Þ
f
f
g
k
¼f
f
g
k
þfd
f
g
k
, ð8:2Þ
and
fg
k
¼fg
k
þfdg
k
ð8:3Þ
As both the internal stresses and the lamina stresses are already known, either
a micromechanical or a macromechanical failure criterion can be employed to detect the
1138
Z.-M. HUANG
at ZHEJIANG UNIV LIB on May 23, 2009 http://jrp.sagepub.comDownloaded from



















