PyPI 官网下载 | pypolyagamma-1.1.5.tar.gz

# PyPólyaGamma [](https://travis-ci.org/slinderman/pypolyagamma) This is a Cython port of Jesse Windle's code at https://github.com/jwindle/BayesLogit. It provides a Python interface for efficiently sampling Pólya-gamma random variates. Install with: pip install pypolyagamma Please open issues if you have any trouble! # Background Pólya-gamma augmentation is a method of performing fast and simple Bayesian inference in models with Gaussian latent variables and count observations. While such models are non-conjugate, if it has the right form (specifically, if it is a Bernoulli, binomial, negative binomial, or multinomial with a logistic link function), we can introduce a set of Pólya-gamma auxiliary variables that render it conditionally conjugate. This facilitates fast Gibbs sampling algorithms on an extended space of Gaussian latent variables and Pólya-gamma auxiliary variables, where integrating out the auxiliary variables leaves the original model intact. Given the auxiliary variables, the latent Gaussian variables have a Gaussian conditional distribution. Likewise, given the Gaussian latent variables and the observed count data, the auxiliary variables have a Pólya-gamma conditional distribution. Thus, to implement the Gibbs sampling algorithm, we must be able to efficiently sample Pólya-gamma random variates. This library provides code to do exactly that. The augmented density, the non-Gaussian marginal, and the Gaussian conditionals are illustrated in the figure below. In this case, the posterior is from a simple binomial model. Next, we'll show how to perform Gibbs sampling for such a model.  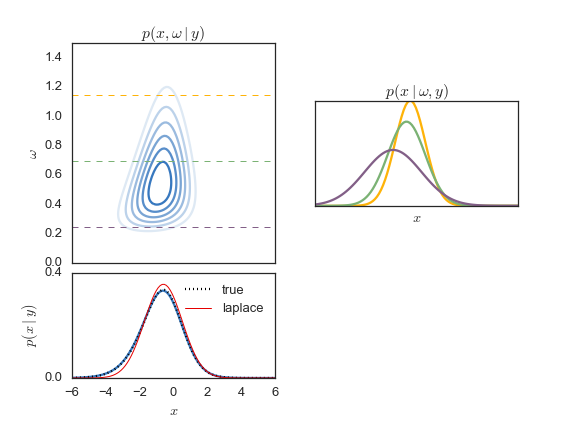See below for more references and links. # Demo For convenience, we have created classes for simple count regression models, like the Bernoulli, binomial, negative binomial, and multinomial (with stick breaking) observation models. For example, you can fit a Bernoulli regression as follows: ```python from pypolyagamma import BernoulliRegression D_out = 1 # Output dimension D_in = 2 # Input dimension reg = BernoulliRegression(D_out, D_in) # Given X, an NxD_in array of real-valued inputs, # and Y, and NxD_out array of binary observations. Fit # the linear model y_n ~ Bern(sigma(A x_n + b)), # where sigma is the logistic function. A is D_out x D_in, # b is D_out x 1, and the entries in y_n are cond. indep. samples = [] for _ in range(100): reg.resample((X,Y)) samples.append((reg.A, reg.b)) ``` Under the hood, this will instantiate Pólya-gamma auxiliary variables and perform conditionally-conjugate Gibbs sampling. We can visualize the inferred parameters in terms of the implied probability for each point in the input space.  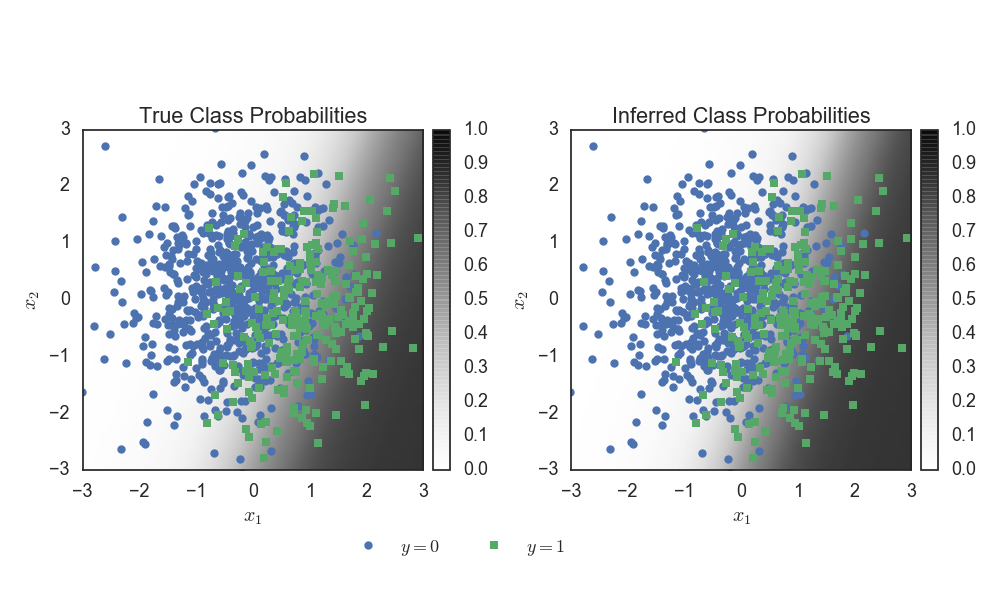Here's how you can manually perform inference in a simple binomial model with `N=10` counts and probability `p=logistic(x)`, with a standard normal prior on `x`. First, sample a count from the model: ```python from pypolyagamma import logistic, PyPolyaGamma # Consider a simple binomial model with unknown probability # Model the probability as the logistic of a scalar Gaussian. N = 10 mu = 0.0 sigmasq = 1.0 x_true = npr.normal(mu, np.sqrt(sigmasq)) p_true = logistic(x_true) y = npr.binomial(N, p_true) ``` Now we can run a Gibbs sampler to estimate the posterior distribution of `x` given `y`. ```python # Gibbs sample the posterior distribution p(x | y) # Introduce PG(N,0) auxiliary variables to render # the model conjugate. First, initialize the PG # sampler and the model parameters. N_samples = 10000 pg = PyPolyaGamma(seed=0) xs = np.zeros(N_samples) omegas = np.ones(N_samples) # Now run the Gibbs sampler for i in range(1, N_samples): # Sample omega given x, y from its PG conditional omegas[i] = pg.pgdraw(N, xs[i-1]) # Sample x given omega, y from its Gaussian conditional sigmasq_hat = 1./(1. / sigmasq + omegas[i]) mu_hat = sigmasq_hat * (mu / sigmasq + (y - N / 2.)) xs[i] = npr.normal(mu_hat, np.sqrt(sigmasq_hat)) ``` For this simple example, we can compute the true posterior and compare the samples to the target density.  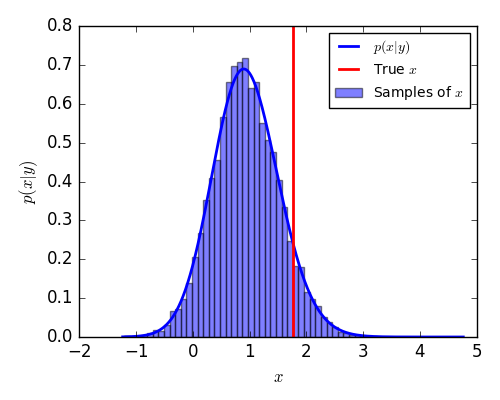# Manual Installation If you're a developer, you can also install from source: git clone git@github.com:slinderman/pypolyagamma.git cd pypolyagamma pip install -e . To check if it worked, run: nosetests If all the tests pass then you're good to go! Under the hood, the installer will download [GSL](https://www.gnu.org/software/gsl/), untar it, and place it in `deps/gsl`. It will then configure GSL and compile the Pólya-gamma code along with the required GSL source files. This way, you don't need GSL to be installed and available on your library path. ## Parallel sampling with OpenMP By default, the simple installation above will not support parallel sampling. If you are compiling with GNU `gcc` and `g++`, you can enable OpenMP support with the flag: USE_OPENMP=True pip install -e . Mac users: you can install `gcc` and `g++` with Homebrew. Just make sure that they are your default compilers, e.g. by setting the environment variables `CC` and `CXX` to point to the GNU versions of `gcc` and `g++`, respectively. With Homebrew, these versions will be in `/usr/local/bin` by default. To sample in parallel, call the `pgdrawvpar` method: ```python n = 10 # Number of variates to sample b = np.ones(n) # Vector of shape parameters c = np.zeros(n) # Vector of tilting parameters out = np.empty(n) # Outputs # Construct a set of PolyaGamma objects for sampling nthreads = 8 seeds = np.random.randint(2**16, size=nthreads) ppgs = [pypolyagamma.PyPolyaGamma(seed) for seed in seeds] # Sample in parallel pypolyagamma.pgdrawvpar(ppgs, b, c, out) ``` If you haven't installed with OpenMP, this function will revert to the serial sampler. # References - [Polson, Nicholas G., James G. Scott, and Jesse Windle. "Bayesian inference for logistic models using Pólya–Gamma latent variables." _Journal of the American statistical Association_ 108.504 (2013): 1339-1349.](http://www.tandfonline.com/doi/pdf/10.1080/01621459.2013.829001) - [Windle, Jesse, Nicholas G. Polson, and James G. Scott. "Sampling Polya-Gamma random variates: alternate and approximate techniques." _arXiv preprint arXiv:1405.0506_ (2014).](http://arxiv.org/pdf/1405.0506) - [Linderman, Scott, Matthew Johnson, and Ryan P. Adams. "Dependent Multinomial Models Made Easy: Stick-Breaking with the Polya-gamma Augmentation." _Advances in Neural Information Processing Systems (NIPS)_. 2015.](http://papers.nips.cc/paper/5660-dependent-multinomial-models-made-easy-stick-breaking-with-the-polya-gamma-augmentation.pdf) Check out our github repo, [pgmult](https://github.com/HIPS/pgmult) - [Linderman, Scott W., Ryan P. Adams, and Jonathan W. Pillow. "Bayesian latent structure discovery from multi-neuron recordings." _Advances in Neural Information Processing Systems (NIPS)_ 2016.](https://arxiv.org/pdf/1610.08465) Check out our github repo, [pyglm](https://github.com/slinderman/pyglm)) - [Linderman, Scott W., Matthew Johnson, Andrew C. Miller, Ryan P. Adams, David M. Blei, and Liam Paninski. "Bayesian learning and inference in recurrent switching linear dynamical systems." _Artificial Intelligence and Statistics (AISTATS)_ 2017.](https://arxiv.org/pdf/1610.08466.pdf)