一讲函数与方程重点二分法PPT课件.pptx
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
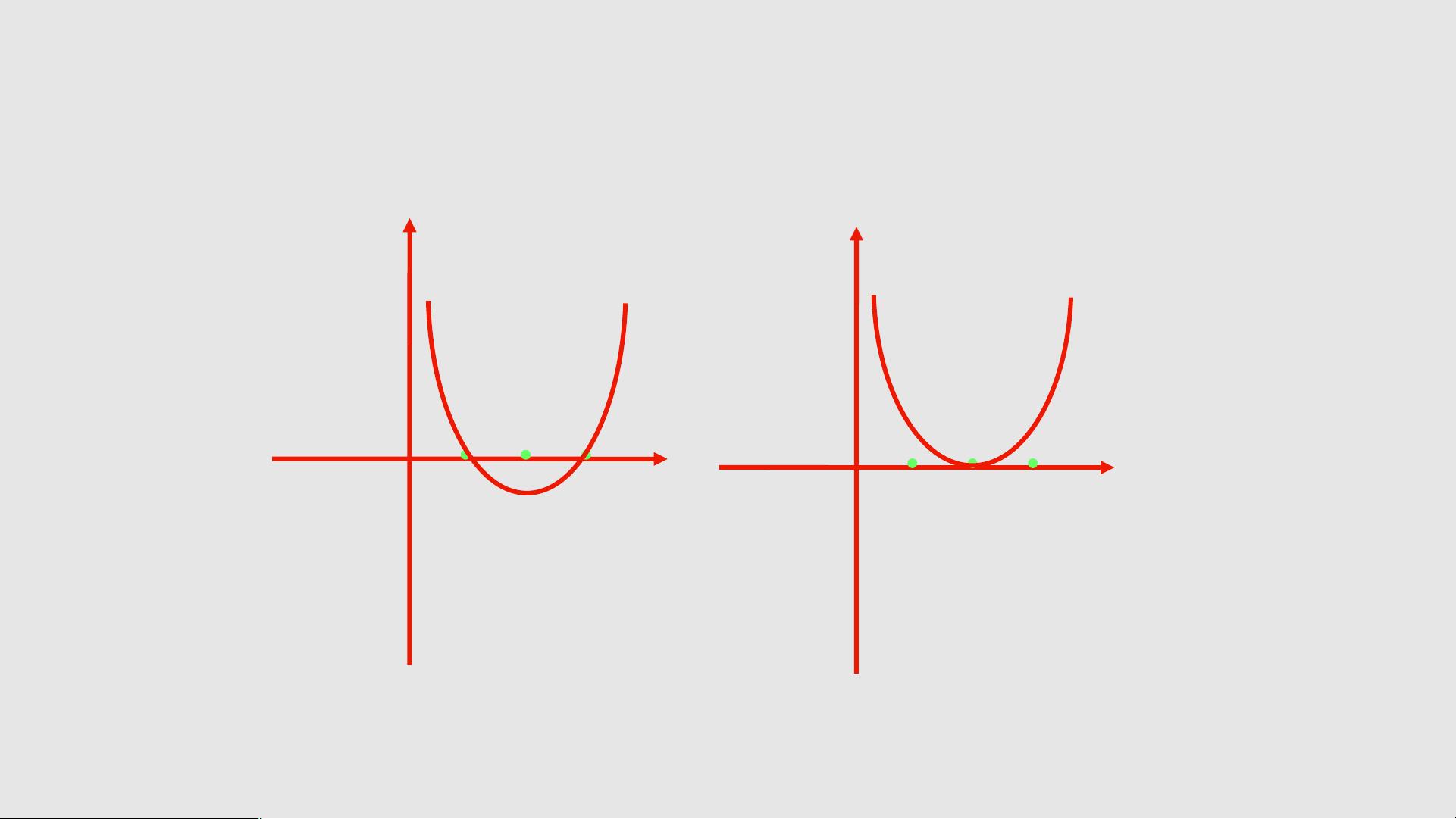
【函数的零点与方程的根】 函数的零点是指函数值等于零的自变量值,即如果函数 \( y=f(x) \) 满足 \( f(x)=0 \),那么 \( x \) 称为该函数的零点。在数学中,函数的零点与方程 \( f(x)=0 \) 的实数根是等价的概念。换句话说,当函数 \( y=f(x) \) 的图像与 \( x \) 轴相交时,交点的横坐标就是函数的零点。 例如,在提供的练习中,我们看到几个简单的函数,如 \( f(x)=2x-4 \) 和 \( f(x)=x^2-4x+3 \),要求求解它们的零点。对于线性函数 \( f(x)=2x-4 \),可以通过解方程 \( 2x-4=0 \) 得到零点;而对于二次函数 \( f(x)=x^2-4x+3 \),可以使用因式分解或者求根公式来找到零点。 **变号零点与零点存在性定理** 变号零点是指函数在某区间两端点的函数值异号,即 \( f(a)f(b)<0 \)。根据零点存在性定理,如果函数在闭区间 [a, b] 上连续,且两端点的函数值异号,则在该区间内至少存在一个变号零点。这意味着函数的图像在区间内必然穿过 \( x \) 轴,即至少有一个实数根。 **二分法求零点** 二分法是一种常用的数值求解方法,用于找到函数变号零点的近似值。具体步骤如下: 1. **确定初始区间**:首先需要确保函数在给定区间 [a, b] 内有变号零点,即 \( f(a)f(b)<0 \)。 2. **取中点**:计算区间中点 \( c = \frac{a+b}{2} \)。 3. **判断中点函数值**:计算 \( f(c) \)。如果 \( f(c)=0 \),那么 \( c \) 就是零点;如果 \( f(c) \) 与 \( f(a) \) 或 \( f(b) \) 符号相反,那么零点在子区间 [a, c] 或 [c, b] 内;如果 \( f(c) \) 与 \( f(a) \) 和 \( f(b) \) 符号相同,那么继续将包含零点的子区间一分为二,重复以上步骤。 4. **循环迭代**:不断重复上述过程,每次都将包含零点的区间长度减半,直到满足所需的精度要求。 **例题解析** 在课件中的例题中,第一个例子展示了如何使用二分法求解三次多项式 \( f(x)=x^3-3x^2+2x-6 \) 在区间 [0, 4] 内的零点。通过计算端点和中点的函数值,最终找到 \( x_2=3 \) 是一个零点。 第二个例子要求求解 \( f(x)=x^3+x^2-2x-2 \) 的一个正零点,精度要求误差不超过 0.1。通过迭代二分法,最终确定区间 [1.375, 1.5] 内的中点 \( x_3=1.438 \) 作为零点的近似值。 **练习解答** 1. 函数 \( f(x)=-x^2+8x-16 \) 在区间 [3, 5] 上有一个零点,因为 \( f(3)f(5)<0 \) 且函数在该区间内连续。 2. 函数 \( f(x)=x^3-2x^2+3x-6 \) 在区间 [-2, 4] 上的变号零点必定在 [-2, 1] 内,因为 \( f(-2)f(1)<0 \),且函数在该区间内连续。 总结来说,二分法是寻找函数零点的有效数值方法,尤其适用于不能直接解析求解的方程。它依赖于函数在特定区间内的连续性和变号性质,通过不断分割区间逼近零点,从而得到零点的近似值。在实际应用中,这种方法被广泛用于科学计算和工程问题的解决。

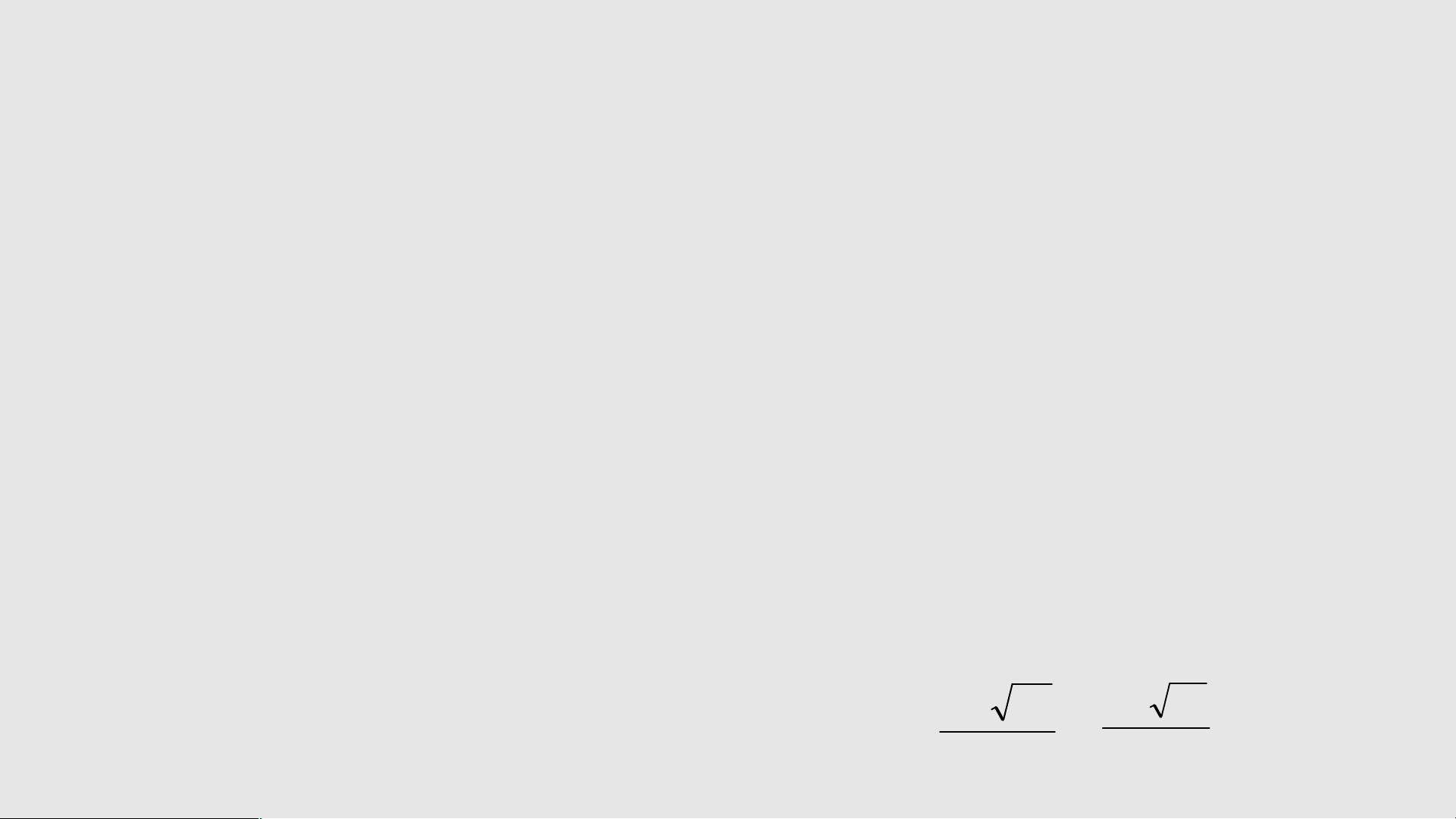
剩余12页未读,继续阅读

- 粉丝: 1401
- 资源: 52万+




 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功