三角形内角和PPT教学课件.pptx

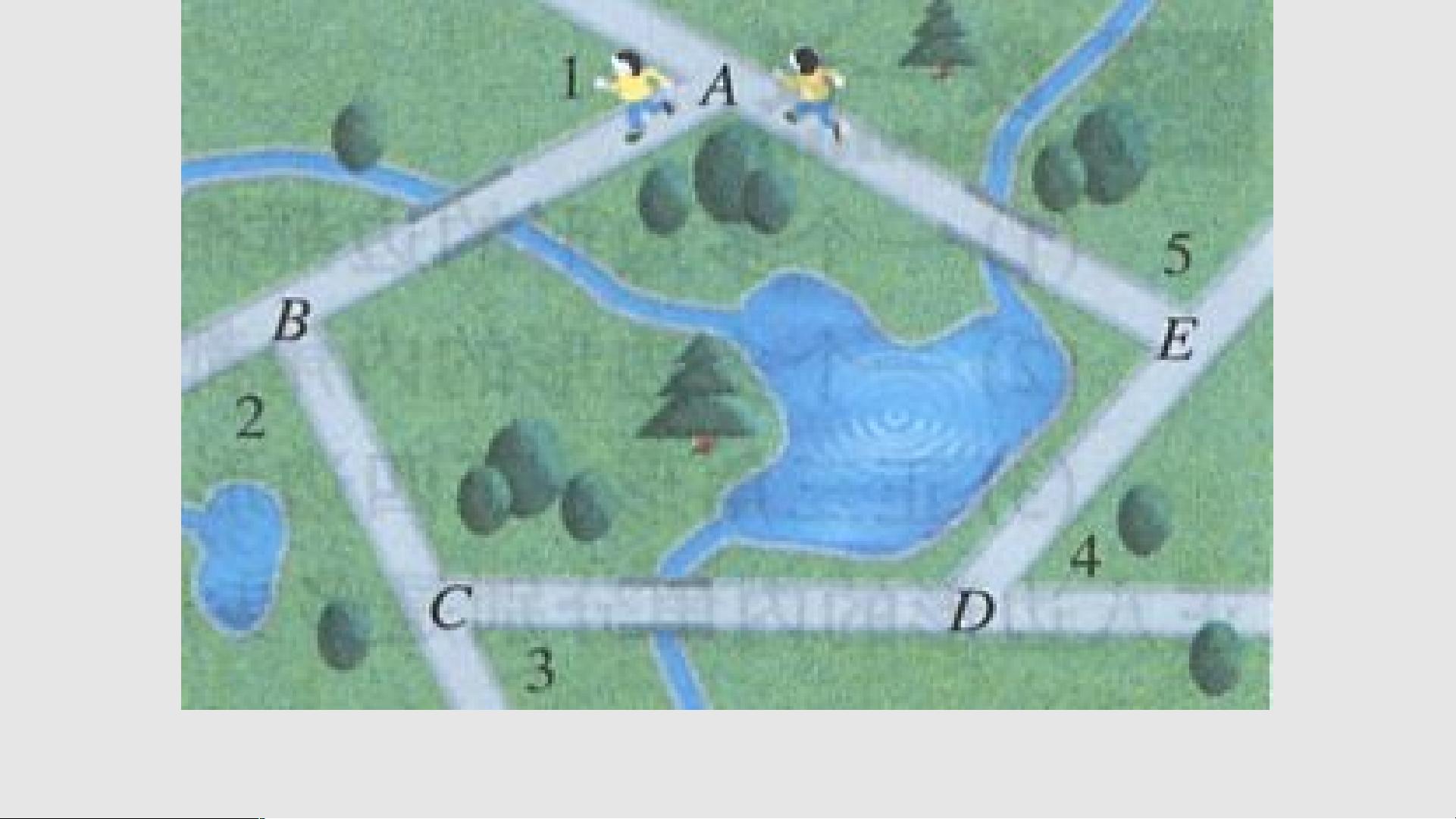
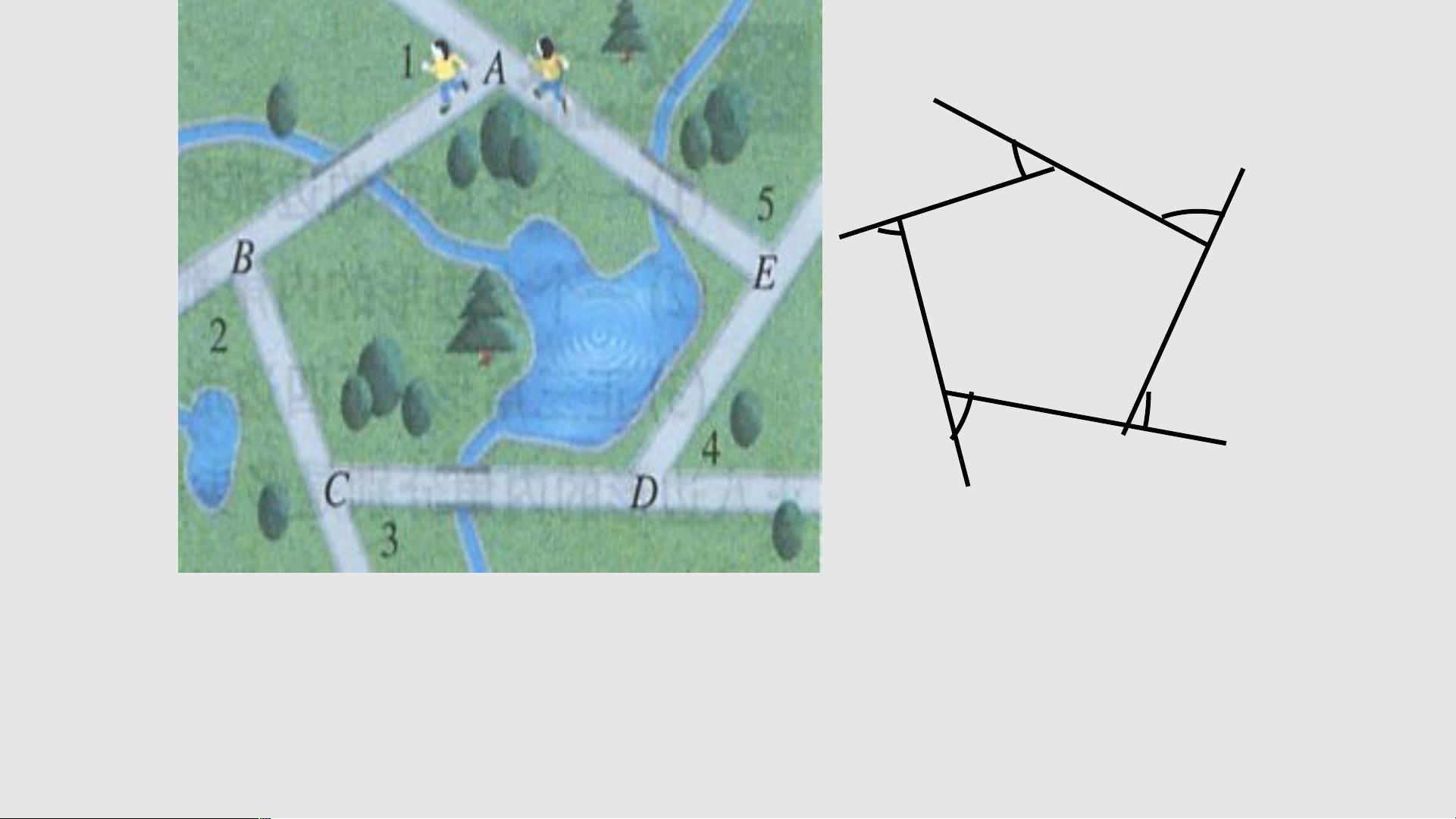
这份PPT教学课件主要讲解了与几何图形相关的知识点，特别是关于三角形和多边形内角和外角的概念及性质。以下是对这些内容的详细解释： 1. **三角形内角和**：三角形内角和是180度。例如，在问题中提到的梁小龙跑步的例子中，即使是在五边形广场周围跑，每转过一个街角，身体转过的角度构成了三角形的内角。当他跑完一圈，这些角度之和加起来会是360度。 2. **多边形的外角和**：多边形的外角和等于360度。以四边形为例，每个顶点处的外角相加总和是360度。这可以通过将多边形的每个内角分为两个相等的角，并与相邻的外角相加来理解，因为每个内角的两半与相应的外角相加总是180度。 3. **三角形的外角性质**：三角形的一个外角等于不相邻的两个内角之和。在图中，∠α、∠β和∠γ分别与三角形内的三个角相对应，它们的和为360度。 4. **四边形的外角和**：四边形的外角和同样也是360度，这可以通过将四边形的每个内角分为两个相等的部分，然后与相邻的外角相加得到。 5. **多边形的外角和**：对于任意多边形，其所有外角的和始终是360度。这意味着五边形、六边形乃至更高边数的多边形，其外角和均为360度。 6. **多边形的内角和与外角和的关系**：多边形的内角和可以通过公式 `(n - 2) × 180` 计算，其中 `n` 是多边形的边数。而外角和总是固定为360度。因此，多边形的内角和与外角和之比可以用来确定多边形的边数。 7. **练习题**：在给出的练习题中，例如第一题要求计算每个外角都是60度的多边形的边数和内角和。根据外角和的性质，我们知道这个多边形的外角和是360度，因此360除以60得到6，所以这是一个六边形。它的内角和是`(6 - 2) × 180 = 720`度。 8. **多边形剪去一个角的情况**：将四边形剪去一个角后，可能会形成新的五边形、四边形或三角形。每种情况下，外角和保持不变，始终为360度。但内角和会相应地改变，具体取决于剪切方式。 通过这些内容的学习，学生可以更好地理解和运用三角形和多边形的内角和外角性质，解决相关的问题。这在基础几何学中是非常重要的概念，有助于培养空间思维和推理能力。