基于双闭环PID控制的一阶倒立摆控制系统SIMULINK仿真设计

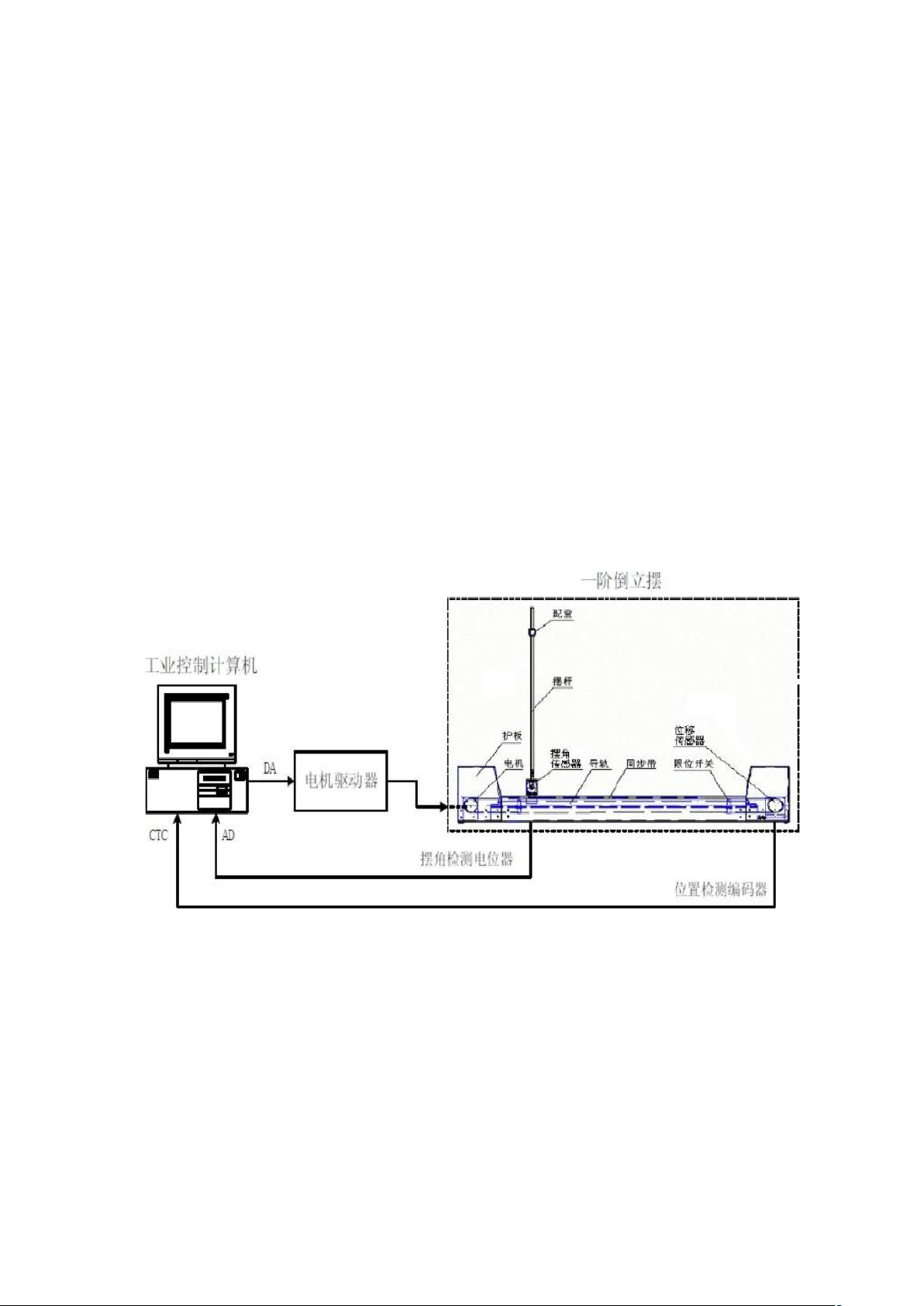
(1)通过理论分析建立对象模型（实际模型），并在原点进行线性化，得到线性化模型；将实际模型和线性化模型作为子系统，并进行封装，将倒立摆的振子质量m和倒摆长度L作为子系统的参数，可以由用户根据需要输入； (2)设计实验，进行模型验证； (3)一阶倒立摆系统为“自不稳定的非最小相位系统”。将系统小车位置作为“外环”，而将摆杆摆角作为“内环”，设计内化与外环的PID控制器； (4)在单位阶跃输入下，进行SIMULINK仿真; (5)编写绘图程序，绘制阶跃响应曲线，并编程求解系统性能指标：最大超调量、调节时间、上升时间； (6)检验系统的鲁棒性：将对象的特性做如下变化后，同样在单位阶跃输入下，检验所设计控制系统的鲁棒性能，列表比较系统的性能指标（最大超调量、调节时间、上升时间）。 倒摆长度L不变，倒立摆的振子质量m从1kg分别改变为1.5kg、2kg、2.5kg、0.8kg、0.5kg； 倒立摆的振子质量m不变，倒摆长度L从0.3m分别改变为0.5m、0.6m、0.2m、0.1m。 ### 基于双闭环PID控制的一阶倒立摆控制系统SIMULINK仿真设计 #### 1. 任务概述 一阶倒立摆控制系统是自动控制领域中的经典问题之一，其核心在于利用适当的控制策略使倒立摆保持稳定状态。本设计以双闭环PID控制策略为核心，通过理论分析建立倒立摆的数学模型，并使用MATLAB/SIMULINK工具进行仿真验证，最终实现对倒立摆系统的有效控制。 #### 2. 系统建模 ##### 2.1 对象模型 倒立摆系统可被视为一个典型的非线性系统，其动态特性受到多种因素的影响，包括但不限于摆的质量\(m\)、摆的长度\(L\)等物理参数。在建立模型时，首先需要考虑的是摆的运动方程，该方程描述了摆的角位置随时间的变化规律。对于一阶倒立摆系统，可以通过牛顿第二定律推导出摆的运动方程： \[ mL^2\ddot{\theta} + mLg\sin{\theta} = u - mL\dot{\theta}^2\sin{\theta} \] 其中，\(\theta\)为摆的角度，\(g\)为重力加速度，\(u\)为施加在小车上的控制力。该方程是非线性的，但在特定条件下（如小角度摆动）可以进行线性化处理，简化后的线性模型为： \[ mL^2\ddot{\theta} + mLg\theta \approx u \] ##### 2.2 模型建立及封装 在MATLAB/SIMULINK中，可以通过构建子系统的方式来实现模型的建立和封装。具体步骤如下： 1. **创建子系统**：在SIMULINK环境中创建一个新的模型文件，然后插入一个子系统模块。 2. **定义参数**：将倒立摆的振子质量\(m\)和倒摆长度\(L\)设置为子系统的参数，用户可以根据需求调整这些参数。 3. **搭建模型**：在子系统内部搭建实际模型和线性化模型，确保两个模型的输入输出端口一致。 4. **封装子系统**：将子系统进行封装，隐藏内部细节，只暴露必要的输入输出接口，便于后续的仿真和调试工作。 #### 3. 仿真验证 ##### 3.1 实验设计 为了验证模型的正确性，需要设计一系列实验来测试不同工况下的系统行为。实验可以包括不同的输入信号（如阶跃、斜坡等），以及改变模型参数（如摆的质量和长度）。 ##### 3.2 建立M文件编制绘图子程序 编写MATLAB脚本来自动化地执行仿真过程并绘制结果。脚本应包含以下功能： - 设置仿真时间和步长。 - 输入仿真数据（例如控制信号）。 - 调用SIMULINK模型进行仿真。 - 绘制仿真结果，如小车的位置和摆的角度随时间的变化曲线。 #### 4. 双闭环PID控制器设计 ##### 4.1 内环控制器的设计 内环控制器主要负责控制摆杆的角度，使其保持在平衡位置。设计内环PID控制器时需要考虑系统的稳定性、响应速度等因素。通过调整PID控制器的比例系数\(K_p\)、积分系数\(K_i\)和微分系数\(K_d\)，可以使系统在阶跃输入下具有良好的动态特性。 ##### 4.2 外环控制器的设计 外环控制器则关注于控制小车的位置。同样地，需要设计一个PID控制器来优化小车的移动轨迹，使其能够快速准确地跟踪给定的位置指令。 #### 5. 仿真实验 ##### 5.1 简化模型 为了方便分析和调试，可以先使用简化模型进行初步的仿真测试。简化模型通常是对复杂模型的近似，可以帮助理解系统的基本行为。 ##### 5.2 仿真实验 在SIMULINK中设置好所有参数后，运行仿真，观察系统的响应情况。特别关注系统的动态特性和稳态误差。 #### 6. 检验系统的鲁棒性 ##### 6.1 编写程序求系统性能指标 编写MATLAB程序来计算系统的性能指标，包括最大超调量、调节时间和上升时间。这些指标反映了系统的稳定性和动态性能。 ##### 6.2 改变参数验证控制系统的鲁棒性 为了验证控制系统的鲁棒性，可以改变系统的一些关键参数，如摆的质量和长度，观察系统响应的变化。具体步骤如下： - **质量变化**：保持倒摆长度\(L\)不变，将振子质量\(m\)从1kg分别改变为1.5kg、2kg、2.5kg、0.8kg、0.5kg。 - **长度变化**：保持振子质量\(m\)不变，将倒摆长度\(L\)从0.3m分别改变为0.5m、0.6m、0.2m、0.1m。 - **性能指标对比**：对于每种情况下，记录系统的最大超调量、调节时间和上升时间，并进行对比分析。 #### 7. 结论 通过对一阶倒立摆控制系统的建模、仿真和性能分析，我们可以得出结论：双闭环PID控制策略能够有效地控制倒立摆系统，即使在参数发生变化的情况下也能保持系统的稳定性和良好的动态性能。此外，通过对系统性能指标的量化分析，进一步证明了该控制策略的鲁棒性和实用性。