1
基于多种方法的系泊系统方案设计
摘要
本文针对系泊系统的状态分析、部件规格设计、方案选择等问题进行合理的数学抽
象建立基于力学平衡的物理模型,应用试算法、二分法、改进的理想点法、遗传算法等
求解方法对模型进行求解得到结果并加以分析。
问题一中,针对物理受力运用改进的集中质量多边形近似法(坐标系分解法)建立
力学模型,选取合适的试算间隔运用试算法编写 C 语言程序进行模型求解,得到在风向
为 0 度,风速为 12 m/s 和 24 m/s 时钢桶和各节钢管的倾斜角度如表 1、锚链形状如图
6、浮标的吃水深度分别为 0.736 m 和 0.751 m 及游动区域半径为 13.8576 m 和 16.9451
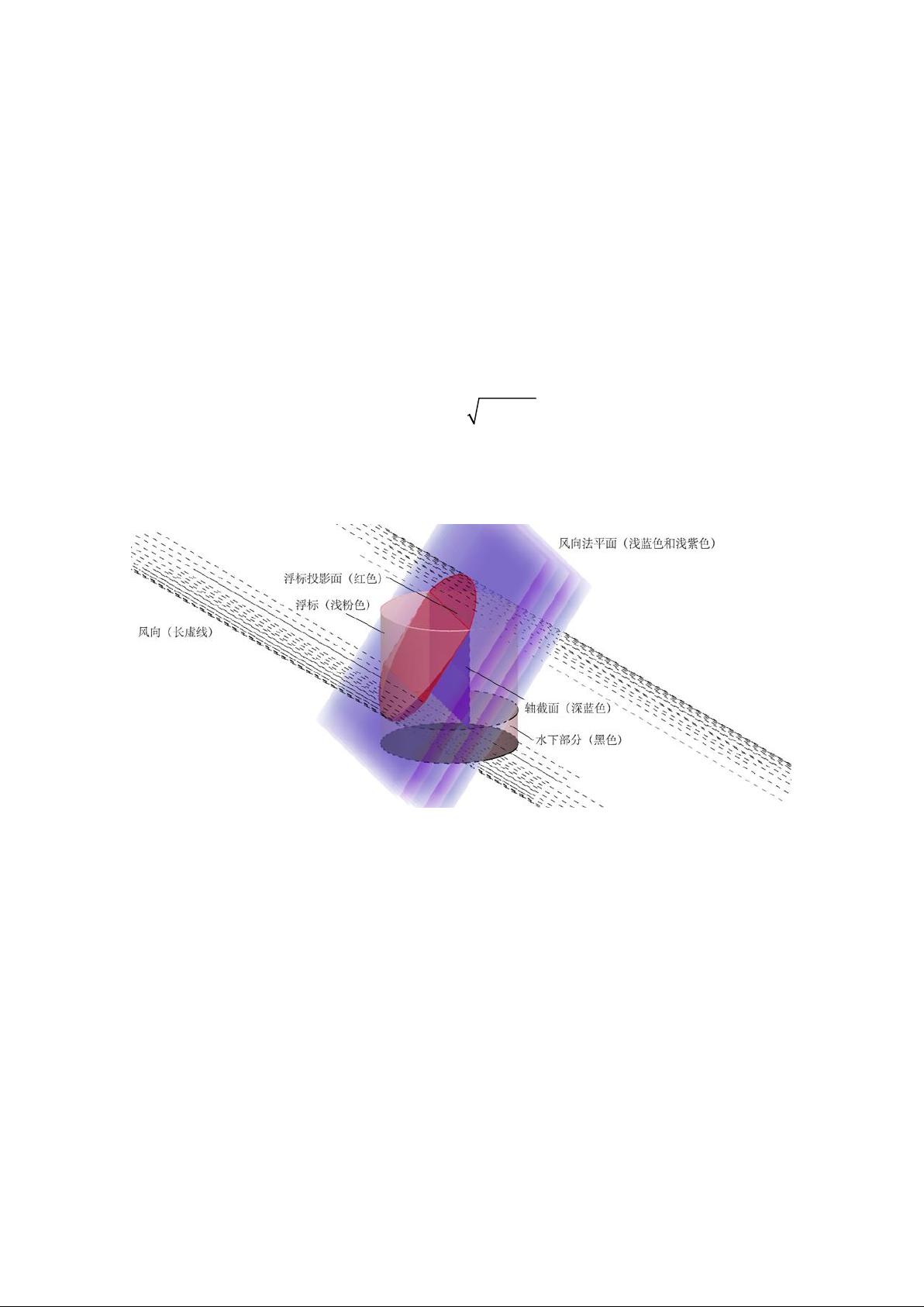
m。物体在风向法平面的投影面与风向有关,讨论后得到各个风向下的上述待求量,本
文展示出浮标吃水深度和游动区域随风向的变化曲线如图 7、9-11,并对规律曲线进行
最大值最小值分析,模型检验采用偏差分析如图 12、13。
问题二中,根据第一问的物理建模,首先试算风速为 3600 m/s,风向为 0 度及重物
球质量为 1200 kg 的系统状态如图 14,表 2,且不满足角度约束,而重物球质量为 3000
kg 时满足角度约束,进而在 1200~3000 kg 范围内由单调性通过二分法得到 2228 kg 时
铁桶和竖直面的夹角达到 86.439 度而锚链末端和海床的夹角为 15.7161 度,为恰好满足
角度的约束条件的重物球的最小质量。对结果左右的值进行角度约束灵敏度分析如图 15,
表 3。
问题三中,在第一问的模型中考虑海水的作用力及物体在海水流法平面的投影面得
到改进的物理模型并进行合理的近似处理,针对系泊系统设计的三个目标通过改进的理
想点算法将多目标转化为单一目标贴近度,在满足钢桶轴线和竖直面的夹角小于 5 度,
锚链末端、海床的夹角小于 16 度、水深介于 16~20 m及锚链不接触海床的四个约束条
件下,给定的风速,水速和风向基础下运用基于二进制编码的遗传算法对锚链型号,锚
链环数目(锚链长度)和重物球质量进行筛选,最后本文仅给出在初始条件风速为 12
m/s,风向为 0 度,海水流速为 1.5 m/s 时符合约束的最优方案,其余初始条件对应的方
案由 EXE 软件呈现。本文展示遗传算法计算 3 次 1000 和 10000 繁衍代数下的所求目标
值如表 5、6。最后通过灵敏度分析对结果可靠性进行检验。
综上所述,本文在对系泊系统深入了解的基础上针对提及的监测系泊系统通过建立
合理的物理模型,运用多种不同的计算算法对体系进行求解并进行深入分析,在得到相
应的结果同时,为深入的研究奠定了基础。
关键字: 试算法 EXE 软件 二分法 改进的理想点算法 遗传算法