第01章 线性规划.pdf
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
【项目资源】:包含前端、后端、移动开发、操作系统、人工智能、物联网、信息化管理、数据库、硬件开发、大数据、课程资源、音视频、网站开发等各种技术项目的源码。包括STM32、ESP8266、PHP、QT、Linux、iOS、C++、Java、python、web、C#、EDA、proteus、RTOS等项目的源码。【项目质量】:所有源码都经过严格测试,可以直接运行。功能在确认正常工作后才上传。【适用人群】:适用于希望学习不同技术领域的小白或进阶学习者。可作为毕设项目、课程设计、大作业、工程实训或初期项目立项。【附加价值】:项目具有较高的学习借鉴价值,也可直接拿来修改复刻。对于有一定基础或热衷于研究的人来说,可以在这些基础代码上进行修改和扩展,实现其他功能。【沟通交流】:有任何使用上的问题,欢迎随时与博主沟通,博主会及时解答。鼓励下载和使用,并欢迎大家互相学习,共同进步。 ### 知识点总结 #### 1. 线性规划概述 - **定义**: 线性规划(Linear Programming, LP)是运筹学的一个重要分支,它涉及在一系列线性约束条件下最大化或最小化一个线性目标函数。 - **历史背景**: 1947年,G.B. Dantzig提出了求解线性规划问题的单纯形方法,这标志着线性规划理论的成熟。 #### 2. 线性规划的应用背景 - **应用场景**: 生产实践中常见的一种问题是如何合理分配资源以获取最大的经济效益,这类问题可以通过线性规划的方法来解决。 - **适用范围**: 线性规划广泛应用于各种技术项目中,如前端、后端、移动开发、操作系统、人工智能、物联网等领域。 #### 3. 线性规划的实际案例分析 - **案例**: 以某机床厂为例,分析如何通过线性规划来决定生产甲、乙两种机床的数量,以使得总利润最大化。 - **数学建模**: - **目标函数**: \(z = 4x_1 + 3x_2\),其中\(x_1\)为甲机床的数量,\(x_2\)为乙机床的数量。 - **约束条件**: - \(x_1 + 2x_2 \leq 10\) - \(x_1 + x_2 \leq 8\) - \(x_2 \leq 7\) - \(x_1, x_2 \geq 0\) #### 4. 决策变量的选择 - **决策变量**: \(x_1\)和\(x_2\)代表甲机床和乙机床的生产数量,它们是解决该问题的关键变量。 - **模型建立**: 建立合适的数学模型对解决问题至关重要,正确选择决策变量是成功建立模型的第一步。 #### 5. 线性规划的Matlab标准形式 - **标准形式**: - 目标函数: \(min\ c^Tx\) - 约束条件: \(A x \leq b, A_{eq} x = b_{eq}, lb \leq x \leq ub\) - **转换规则**: 当原问题的目标函数为最大化时,可以通过取负数的方式转换为目标函数最小化。 #### 6. 线性规划问题的解的概念 - **可行解**: 满足所有约束条件的解。 - **最优解**: 在所有可行解中使目标函数值最大或最小的解。 - **可行域**: 所有可行解构成的集合。 - **顶点**: 可行域的边界上的点,线性规划问题的最优解通常位于可行域的顶点处。 #### 7. 线性规划的图解法 - **图解示意图**: 通过绘制目标函数等位线和平面直角坐标系内的约束条件图形,可以直观地找出最优解的位置。 - **最优解的确定**: 对于二维线性规划问题,最优解通常位于可行域的边界上或顶点处。 #### 8. 线性规划问题的可能状态 - **空集**: 如果没有任何解满足所有的约束条件,则线性规划问题的解集为空集。 - **有界解**: 存在有限的最优解。 - **无界解**: 如果目标函数值无限增加或减少,不存在有限的最优解。 #### 9. 线性规划的实际应用 - **应用领域**: 线性规划在制造业、物流、财务规划、资源分配等多个领域都有广泛应用。 - **软件工具**: 使用如Matlab等工具可以帮助快速构建和求解线性规划模型。 #### 10. 学习资源 - **资源推荐**: 提供了多种技术项目的源码,涵盖前端、后端、移动开发等多个领域。 - **项目质量**: 所提供的源码都经过严格测试,可以直接运行。 - **适用对象**: 适合初学者和进阶学习者,可以作为课程设计、毕设项目的基础。 线性规划是一种非常实用的数学工具,不仅可以帮助我们在复杂的决策环境中做出最优选择,而且在实际工程项目中也有着广泛的应用前景。通过学习线性规划的相关知识和技术,可以有效地提高解决问题的能力,并在多个行业中发挥重要作用。


剩余14页未读,继续阅读

- 粉丝: 1w+
- 资源: 4万+




 我的内容管理
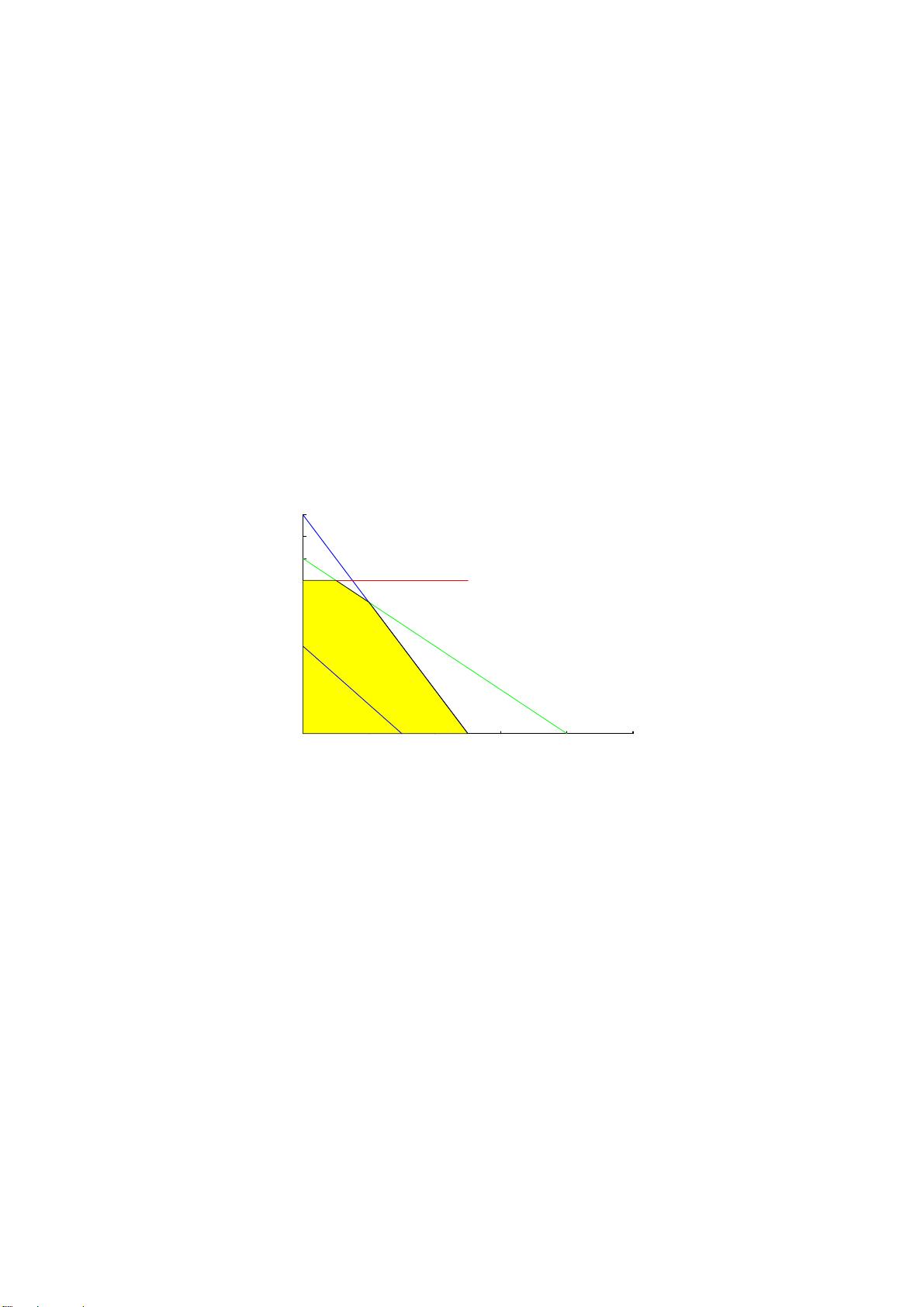
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- java浏览器(使用VSCode)
- PHPThinkphp+Vue2.0前后端分离框架通用后台源码数据库 MySQL源码类型 WebForm
- 构建一个大模型训练、微调、评估、推理、部署的全流程开发套件,基于MindSpore内置的并行技术和组件化设计
- 基于SpringCloud+Vue的财务数据管理系统(后端代码)
- 基于SpringBoot+Vue的在线课程管理系统(前端代码)
- 基于SpringBoot+Vue的在线课程管理系统(后端代码)
- MindInsight为MindSpore提供了简单易用的调优调试能力 用于模型优化的可视化仪表板
- 野火霸道开发板485原工程
- 国产化自主可控的人工智能开源平台 平台面向人工智能研究中的数据处理、算法开发、模型训练、算力管理和推理应用等各个流程的技术难点
- 基于Springboot+Vue的江西红色旅游景点宣传网站(后端代码)


 信息提交成功
信息提交成功