微分+蒙特卡洛+蒙卡

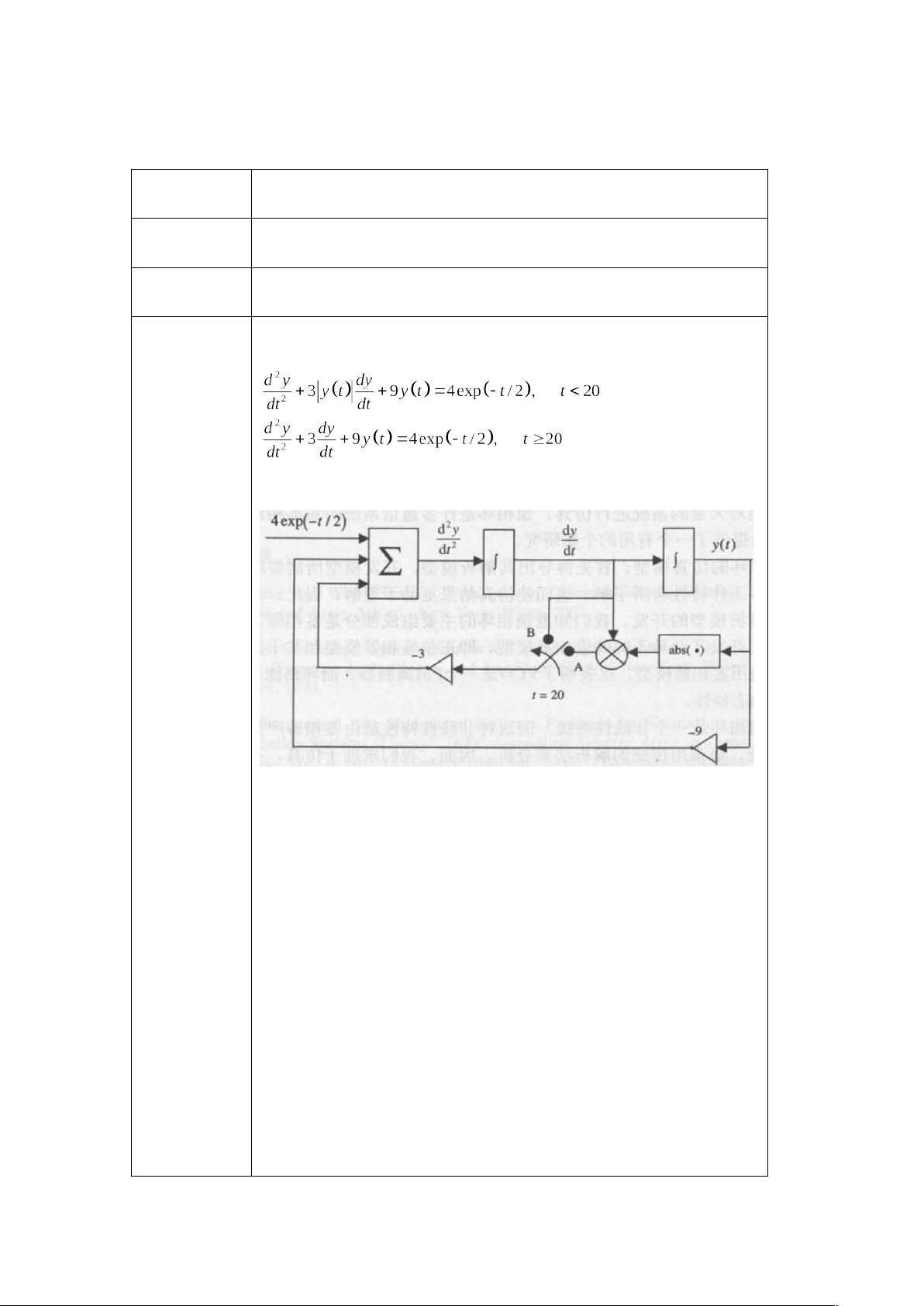
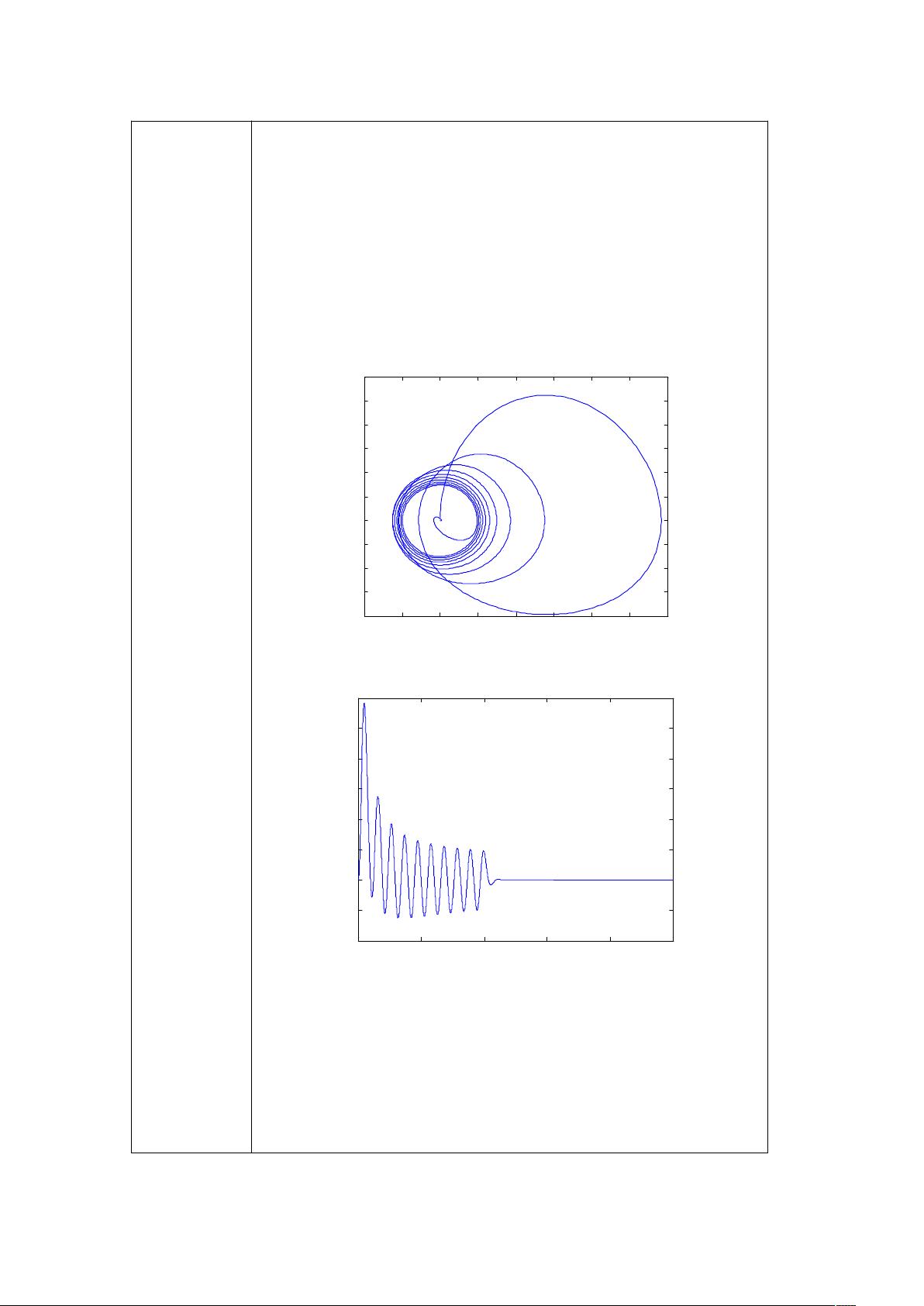
根据给定的信息，我们可以将知识点概括为以下几个方面： ### 一、微分方程与计算机仿真 #### 1. 微分方程简介 - **定义**：微分方程是一种数学模型，用来描述物理系统随时间变化的行为。在工程、物理和其他科学领域中广泛应用。 - **类型**：微分方程可以分为普通微分方程(ODEs)和偏微分方程(PDEs)。本实验主要涉及的是ODEs。 #### 2. 计算机仿真求解 - **目的**：通过计算机编程语言来模拟微分方程的解，从而预测系统的动态行为。 - **方法**：常用的方法包括欧拉法、龙格-库塔法等数值积分技术。 - **工具**：MATLAB是一种常用的软件工具，适用于科学计算、算法开发以及数据分析等领域，尤其适合解决微分方程问题。 ### 二、实验内容详解 #### 实验一：求解微分方程 - **微分方程**： \[ \frac{d^2y}{dt^2} = 4e^{-\frac{t}{2}} - 3\left|\frac{dy}{dt}\right|y - 9y \] 当 \(t < 20\) 时；当 \(t \geq 20\) 时，方程简化为 \[ \frac{d^2y}{dt^2} = 4e^{-\frac{t}{2}} - 3\frac{dy}{dt} - 9y \] - **实验代码解析**： - 初始化变量：设置初始条件和仿真参数。 - 模拟循环：通过迭代计算每个采样点上的状态值。 - 输出结果：记录每个时间点的 \(\frac{dy}{dt}\) 和 \(y(t)\) 的值。 #### 实验二：分析系统的稳定性 - **微分方程**： \[ \frac{d^2x}{dt^2} = 20\sin(2t) - 8x - 4\frac{dx}{dt} \] - **实验代码解析**： - 相同的初始化过程。 - 使用相同的方法进行数值积分。 - 绘制相平面图和 \(x(t)\) 随时间变化的波形图。 - **稳定性分析**： - 观察相平面图的形状来判断系统是否稳定。 - 分析 \(x(t)\) 波形图的变化趋势，判断是否存在稳定的周期性或者收敛行为。 ### 三、蒙特卡洛方法的应用 虽然实验描述中没有明确提到蒙特卡洛方法的具体应用，但基于题目中的关键词“蒙特卡洛”，我们可以推测它可能被用于以下几个方面： - **参数估计**：通过随机抽样来估计微分方程中的未知参数。 - **不确定性分析**：利用蒙特卡洛模拟来评估系统性能受到随机输入影响时的不确定性。 - **敏感性分析**：确定哪些参数对系统行为的影响最大。 ### 四、总结 本实验旨在通过计算机仿真的方法求解微分方程，并利用MATLAB作为主要工具来进行实验。通过对两个具体的微分方程进行求解和稳定性分析，不仅可以加深对微分方程理论的理解，还能提高编程能力并掌握使用MATLAB进行科学计算的方法。此外，尽管实验中未直接涉及到蒙特卡洛方法的应用，但该方法在处理复杂的微分方程问题时具有广泛的应用前景，值得进一步研究和探索。