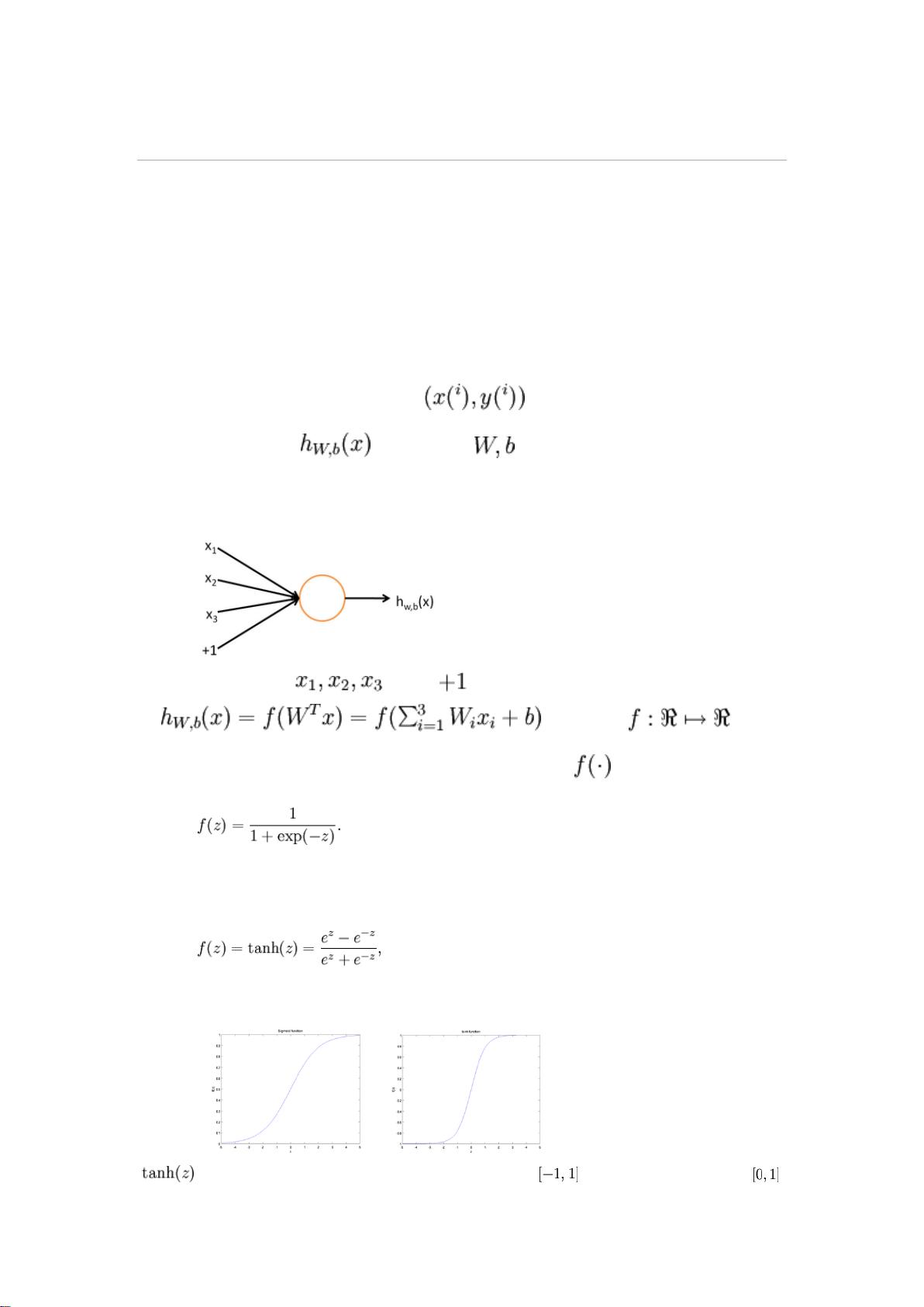
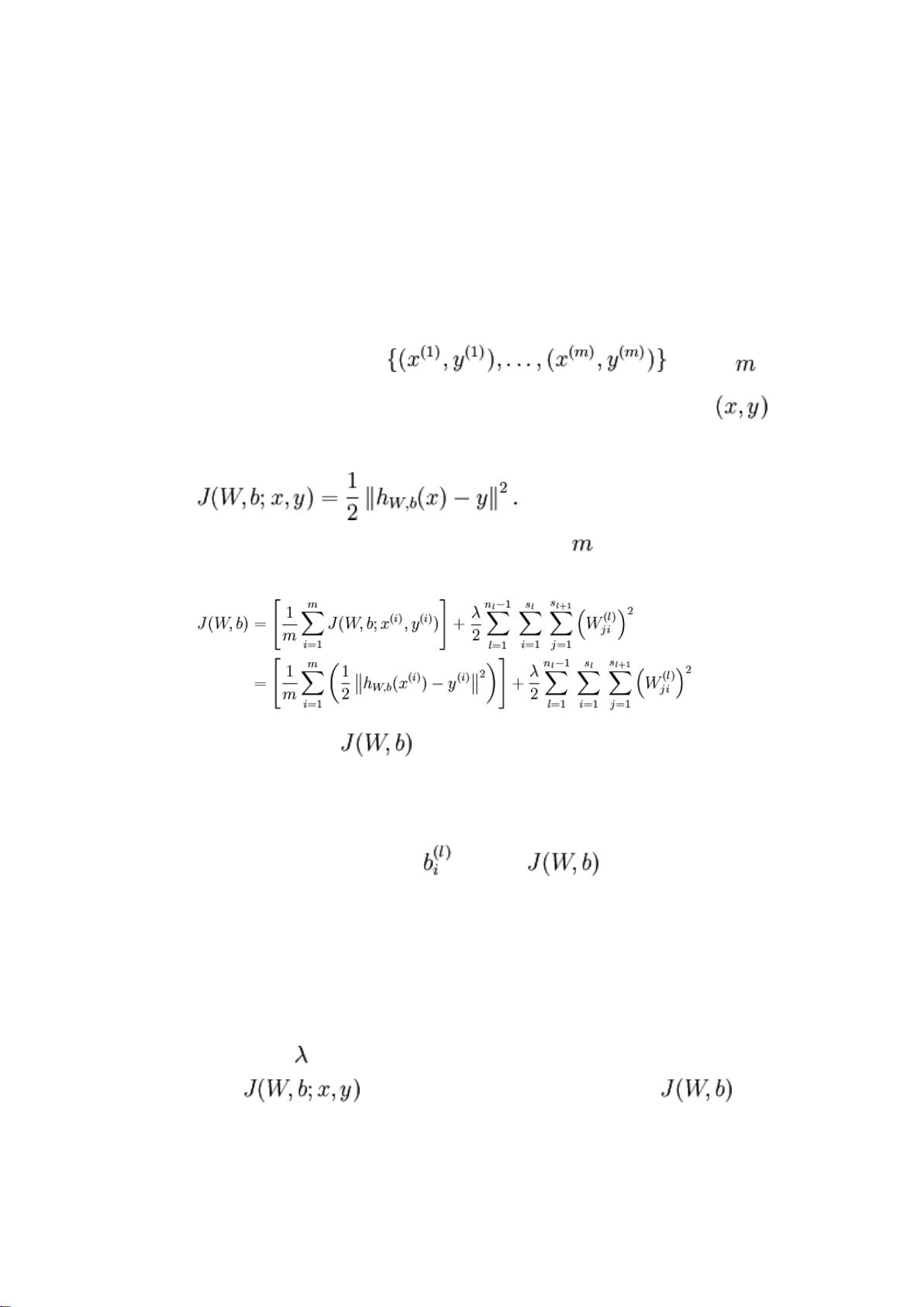
UFLDL 教程-深度神经网络

### UFLDL 教程-深度神经网络 #### 概述 本文档旨在介绍无监督特征学习和深度学习的核心概念，特别关注深度神经网络。通过本教程的学习，读者不仅能掌握核心理论，还将学会如何实现并调整相关的算法。教程假定读者具备一定的机器学习基础知识。 #### 第一章：稀疏自编码器与神经网络基础 ##### 神经网络的基本概念 神经网络是一种模拟人脑神经元结构的计算模型，广泛应用于各种复杂的分类、回归和聚类任务。以监督学习为例，假设我们有一组训练样本集 \(\{(x^{(i)}, y^{(i)})\}_{i=1}^m\)，其中 \(x^{(i)}\) 是输入特征向量，\(y^{(i)}\) 是对应的标签。神经网络能提供一个复杂且非线性的假设模型 \(h_{\theta}(x)\) 来近似这些数据，其中 \(\theta\) 表示模型的参数。 ##### 单一神经元的模型 让我们从最简单的神经网络——仅含一个“神经元”的网络开始介绍。这个神经元接受输入 \(x_1, x_2, \ldots, x_n\) 和一个额外的截距项 \(x_0 = 1\)，并通过一个激活函数 \(f\) 计算输出 \(a\)。在本教程中，我们通常选用 sigmoid 函数作为激活函数： \[ f(z) = \frac{1}{1 + e^{-z}} \] 此外，还可以考虑使用双曲正切函数 (tanh) 作为激活函数： \[ f(z) = \tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} \] 这两个函数都具有平滑且非线性的特性，使得神经网络能够捕获数据中的复杂关系。值得注意的是，sigmoid 函数的导数为： \[ f'(z) = f(z)(1-f(z)) \] 而 tanh 函数的导数为： \[ f'(z) = 1 - [f(z)]^2 \] 这些导数在后续的反向传播过程中非常关键。 ##### 多层神经网络 多层神经网络是通过将多个神经元以特定的方式连接起来构成的。例如，考虑一个简单的神经网络，该网络由输入层、一个隐藏层和一个输出层组成： - 输入层：包含 \(n\) 个节点，用于接收输入数据。 - 隐藏层：位于输入层和输出层之间，包含若干节点（隐藏单元），这些节点不直接与外部环境交互。 - 输出层：包含 \(k\) 个节点，用于输出最终结果。 对于一个具有 \(L\) 层的神经网络，我们将其记为 \(\{l_1, l_2, \ldots, l_L\}\)，其中 \(l_1\) 代表输入层，\(l_L\) 代表输出层，而 \(l_2, l_3, \ldots, l_{L-1}\) 分别代表各隐藏层。每个层的节点数分别为 \(s_1, s_2, \ldots, s_L\)（不包括偏置节点）。 神经网络中的每个连接都有一个权重 \(w\)，以及每个隐藏单元还有一个偏置项 \(b\)。权重和偏置项共同决定了网络的输出。 ##### 前向传播 前向传播是神经网络中的一个核心过程，用于计算从输入层到输出层的值。假设我们已经确定了网络的参数 \(\theta\)，则可以使用前向传播算法来计算每一层的激活值 \(a^{(l)}\)。具体来说，对于任意层 \(l\)，其激活值可以通过以下步骤计算： 1. **计算加权和**：对于第 \(l\) 层中的每个单元 \(j\)，计算加权和 \(z_j^{(l)} = \sum_{i=1}^{s_{l-1}} w_{ji}^{(l-1)} a_i^{(l-1)} + b_j^{(l)}\)。 2. **应用激活函数**：计算 \(a_j^{(l)} = f(z_j^{(l)})\)。 通过重复上述过程，直到最后一层，即可得到网络的输出值。 ##### 参数矩阵化 为了简化计算，可以将权重和偏置项矩阵化，从而利用高效的线性代数运算。例如，对于第 \(l\) 层到第 \(l+1\) 层的连接，可以定义权重矩阵 \(W^{(l)}\) 和偏置向量 \(b^{(l)}\)，然后通过矩阵乘法计算下一层次的加权和 \(Z^{(l+1)} = W^{(l)}A^{(l)} + b^{(l)}\)，其中 \(A^{(l)}\) 是当前层的激活值矩阵。 #### 第二章：反向传播算法 在了解了神经网络的基本结构之后，接下来讨论如何调整网络参数以最小化训练误差。对于给定的训练集 \(\{(x^{(i)}, y^{(i)})\}_{i=1}^m\)，可以通过批量梯度下降法来优化神经网络的参数。具体而言，对于单个训练样例 \((x^{(i)}, y^{(i)})\)，可以定义代价函数 \(J(\theta)\) 如下： \[ J(\theta) = \frac{1}{2} \sum_{k=1}^{K} (h_{\theta}(x^{(i)})_k - y_k^{(i)})^2 \] 其中 \(h_{\theta}(x^{(i)})\) 是神经网络对于输入 \(x^{(i)}\) 的输出，\(y_k^{(i)}\) 是对应的期望输出。对于整个训练集，总代价函数 \(J(\theta)\) 为所有训练样例的平均代价： \[ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} \sum_{k=1}^{K} (h_{\theta}(x^{(i)})_k - y_k^{(i)})^2 \] 为了最小化 \(J(\theta)\)，需要计算每个参数的梯度 \(\frac{\partial J(\theta)}{\partial \theta_{ij}^{(l)}}\)，这一过程可以通过反向传播算法实现。反向传播算法利用链式法则和前向传播时计算的激活值，高效地计算每个参数的梯度，进而更新网络的权重和偏置项。 通过这种方式，神经网络能够自动地调整其参数，以达到最小化训练误差的目的。随着迭代次数的增加，网络的性能会逐渐提高，直至收敛到一个局部最优解。 ### 总结 本章节介绍了无监督特征学习和深度学习的基础知识，重点讲述了深度神经网络的基本结构、前向传播和反向传播算法。这些基础知识为后续深入探索更复杂的神经网络模型奠定了坚实的基础。通过实践这些算法，读者将能够更好地理解和应用深度学习技术解决实际问题。