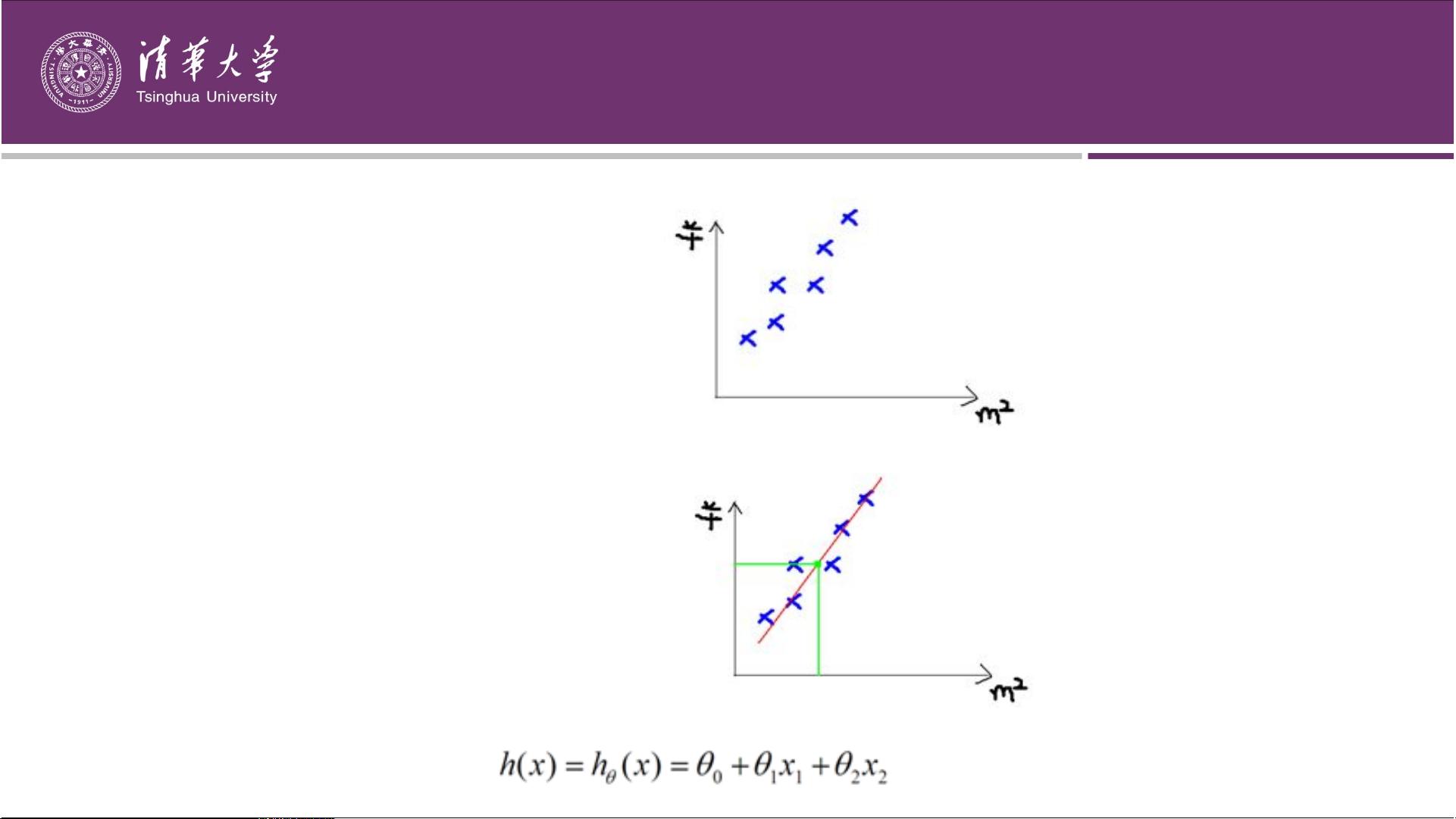
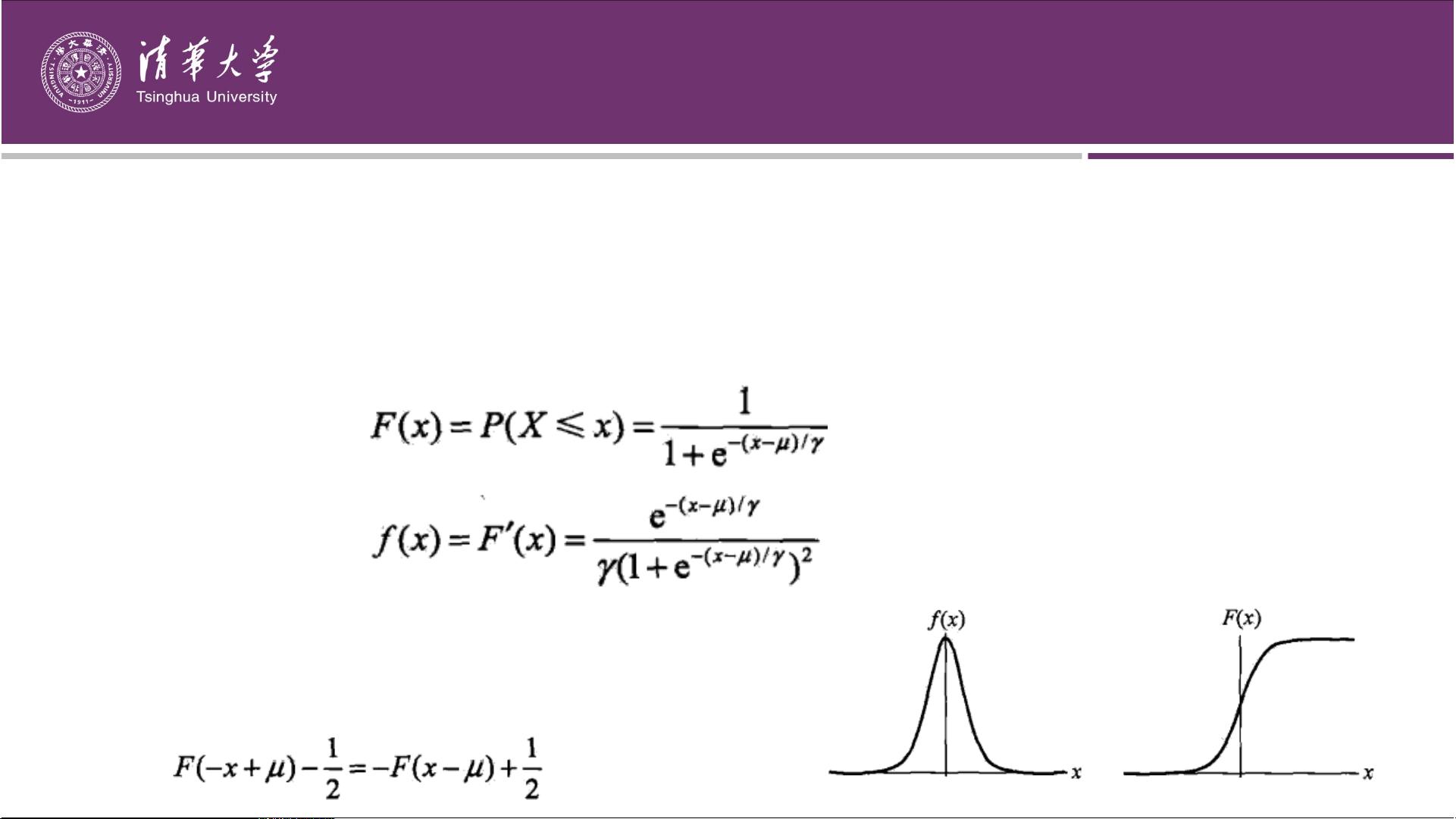
【课程简介】
本课程适合所有需要学习机器学习技术的同学，课件内容制作精细，由浅入深，适合入门或进行知识回顾。
本章为该课程的其中一个章节，如有需要可下载全部课程
全套资源下载地址：https://download.csdn.net/download/qq_27595745/85252312
【全部课程列表】
第1章 机器学习和统计学习 共75页.pptx
第2和12章 感知机和统计学习方法总结 共27页.pptx
第3章 k-近邻算法 共69页.pptx
第4章 贝叶斯分类器 共79页.pptx
第5章 决策树 共98页.pptx
第6章 Logistic回归 共75页.pptx
第7章 SVM及核函数 共159页.pptx
第8章 adaboost 共75页.pptx
第9章 EM算法 共48页.pptx
第10章 隐马尔科夫模型 共64页.pptx
第11章 条件随机场 共63页.pptx
第13章 无监督学习概论 共27页.pptx
第14章 聚类方法 共52页.pptx
第15章 奇异值分解 共66页.pptx
第16章 主成分分析 共67页.pptx
第17章 潜在语义
【Logistic回归与最大熵模型】是机器学习中两种重要的分类方法，它们在处理二分类或多分类问题时具有广泛的应用。Logistic回归是基于广义线性模型的一种方法，其特点是输出连续值，但经过Sigmoid函数转换后，输出值位于(0,1)之间，适合用于预测事件发生的概率。
**Logistic回归**
1. **Sigmoid函数**：Logistic回归的核心是Sigmoid函数，它将任意实数值映射到(0,1)区间，形如1/(1+e^(-x))，曲线呈S型，也称为逻辑斯蒂函数。
2. **二项逻辑斯蒂回归**：适用于二分类问题，通过将线性回归的连续输出转换为概率值，即通过Sigmoid函数。它建立在事件发生的几率(odds)基础上，通过计算对数几率(log-odds)来估计模型参数。
3. **似然函数与极大似然估计**：在Logistic回归中，通过极大似然函数找到最优的模型参数。似然函数是参数的函数，表示给定参数下观测数据出现的概率，最大化似然函数能找出最合理的参数估计。
**最大熵模型(Maximum Entropy Model)**
1. **最大熵原理**：在满足特定约束条件下，熵最大的概率模型被认为是最优的。熵是衡量模型不确定性的量，均匀分布具有最大熵。
2. **多项逻辑回归**：当面临多分类问题时，可以使用多项逻辑回归，它扩展了二项逻辑回归的概念，模型参数估计方法与二项逻辑回归类似。
3. **特征函数与约束最优化**：最大熵模型的学习过程通常涉及到特征函数，通过约束最优化问题寻找满足所有约束条件并具有最大熵的模型。特征函数的期望值在模型与经验分布之间相等，形成模型学习的优化目标。
**学习过程**
1. **梯度下降法**：在模型参数估计过程中，常使用梯度下降法来优化似然函数，寻找使函数值最大化的参数值。
2. **拟牛顿法**：另一种优化方法，通过迭代更新参数，快速逼近局部最优解，适用于非凸优化问题。
这些概念在机器学习课程中是基础且重要的，对于理解和应用机器学习算法，特别是分类问题，至关重要。学习者可以通过深入理解Logistic回归和最大熵模型的原理，结合实际数据集进行实践，从而掌握这些模型的使用技巧。课程中提供的课件详细介绍了每个主题，帮助初学者逐步掌握这些理论知识。
VIP享7折，此内容立减4.47元 
