T-SNE算法介绍

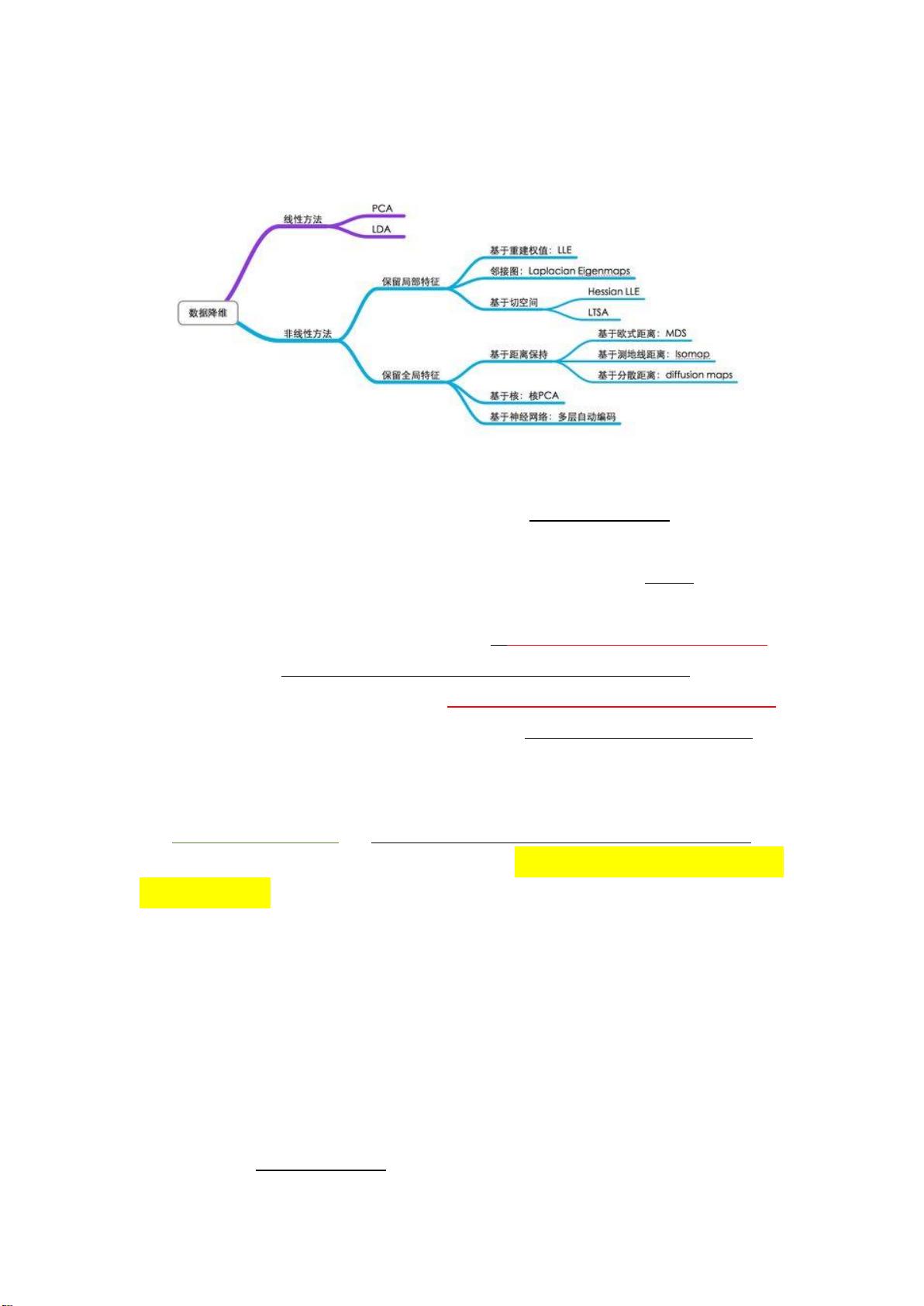
t-SNE(t-distributed stochastic neighbor embedding)：t分布随机邻域嵌入是用于高维数据的降维算法，是由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出来。此外，t-SNE 是一种非线性降维算法，非常适用于高维数据降到2维或者3维，进行可视化。 ### T-SNE算法详解 #### 一、T-SNE算法简介 T-SNE（t-distributed Stochastic Neighbor Embedding）是一种非线性降维技术，主要用于高维数据的可视化。该算法由Laurens van der Maaten和Geoffrey Hinton在2008年提出。相较于传统的降维方法如PCA（Principal Component Analysis），T-SNE能够更好地保留数据的局部结构，非常适合将高维数据降至二维或三维进行可视化。 #### 二、T-SNE的关键特性 1. **非线性降维**：T-SNE是一种非线性降维方法，能够捕获数据集中的复杂非线性结构，这对于高维数据的降维尤为重要。相比之下，PCA等线性方法无法捕捉特征之间的复杂关系。 2. **保持局部结构**：T-SNE着重于保持数据点之间的局部相似性，这意味着即使在低维空间中，相邻的数据点也应尽可能地保持相近。 3. **非参数模型**：T-SNE是一种非参数模型，这意味着它不会学习一组固定的参数来拟合数据。相反，它根据数据点之间的相互关系动态调整其表示。 #### 三、T-SNE的工作原理 T-SNE的工作流程可以分为以下几个步骤： 1. **计算高维空间中的相似度**：T-SNE计算每个数据点与其他数据点之间的高维相似度。这种相似度通常是通过高斯核来计算的，高斯核的带宽σ可以根据数据点的位置自适应地调整，以确保每个数据点都有相似数量的邻居。 2. **计算低维空间中的相似度**：接下来，T-SNE在低维空间中为每个数据点分配一个位置，并计算这些位置之间的相似度。与高维空间不同，低维空间中的相似度通常采用t分布而不是高斯分布，这是因为t分布更有利于数据点之间的聚集，从而更好地保持局部结构。 3. **最小化相似度差异**：T-SNE的目标是最小化高维空间和低维空间中相似度分布之间的差异。这一过程通常通过梯度下降法实现，旨在使高维空间中的相似点在低维空间中也保持相似。 #### 四、SNE与T-SNE的关系 T-SNE是从SNE（Stochastic Neighbor Embedding）发展而来的。SNE的基本思想是将高维数据点之间的相似度映射到低维空间中，以保持数据点间的相对距离。然而，SNE存在“crowding problem”（拥挤问题），即在低维空间中难以同时保持数据点之间的全局结构和局部结构。为了解决这个问题，T-SNE引入了t分布，有效地缓解了拥挤问题，并提高了算法的性能。 #### 五、T-SNE的应用场景 T-SNE因其优秀的可视化能力和非线性的特性，被广泛应用于各种高维数据集的分析中，包括但不限于： - **图像处理**：如面部表情识别。 - **自然语言处理**：例如使用Word2Vec进行文本比较。 - **基因组数据分析**：如识别肿瘤亚群。 - **语音处理**：如语音识别和分类。 #### 六、总结 T-SNE作为一种高效的降维和可视化工具，在处理复杂高维数据时表现出色。通过对数据点之间的相似性进行建模，T-SNE能够在低维空间中保持数据的局部结构，从而为数据科学家提供了深入理解数据模式的有效手段。尽管T-SNE在某些方面存在局限性，如计算成本较高以及可能存在的过度拥挤问题，但它仍然是当前数据分析领域不可或缺的重要工具之一。