第五章 解析结构模型.ppt

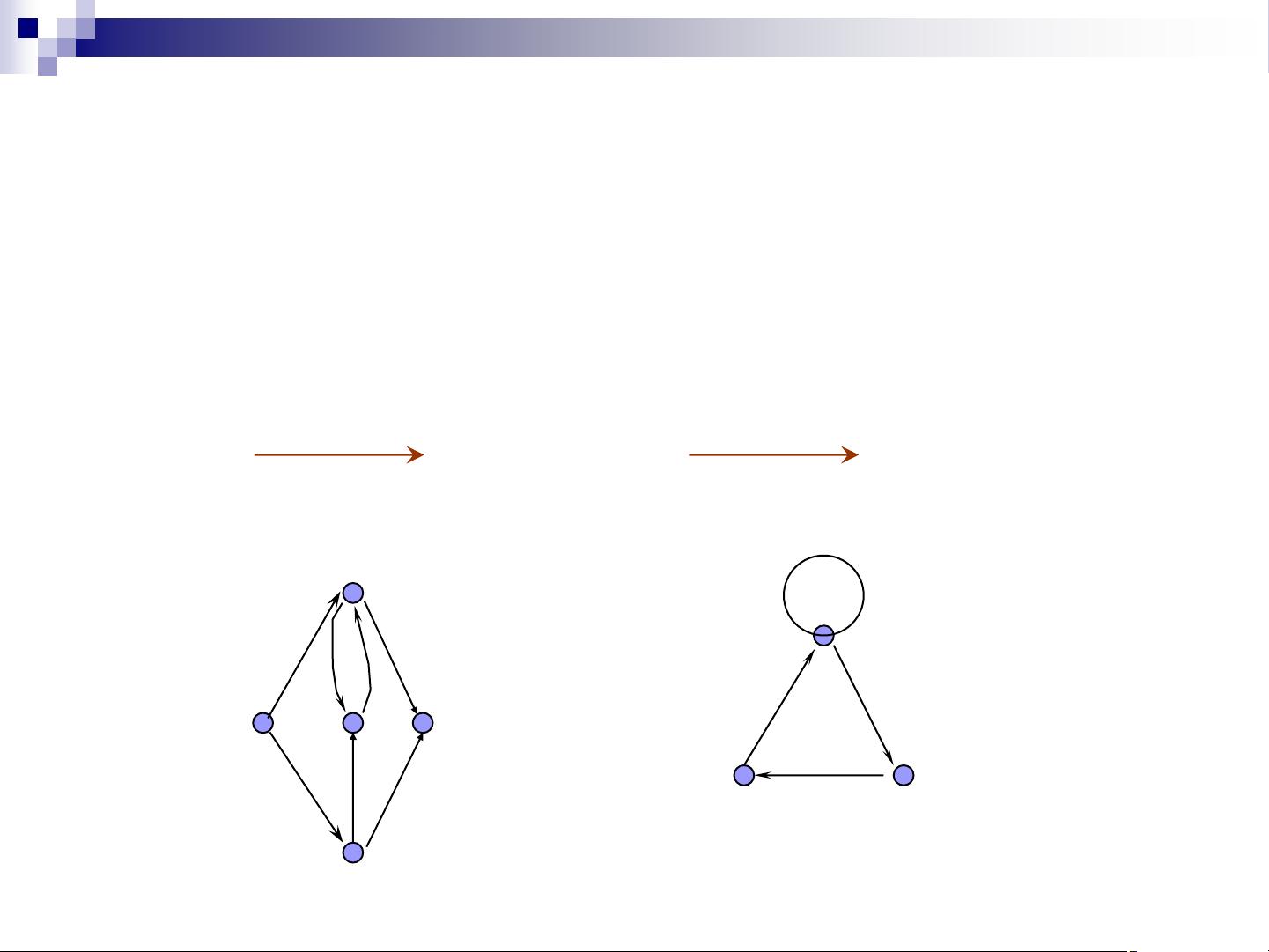
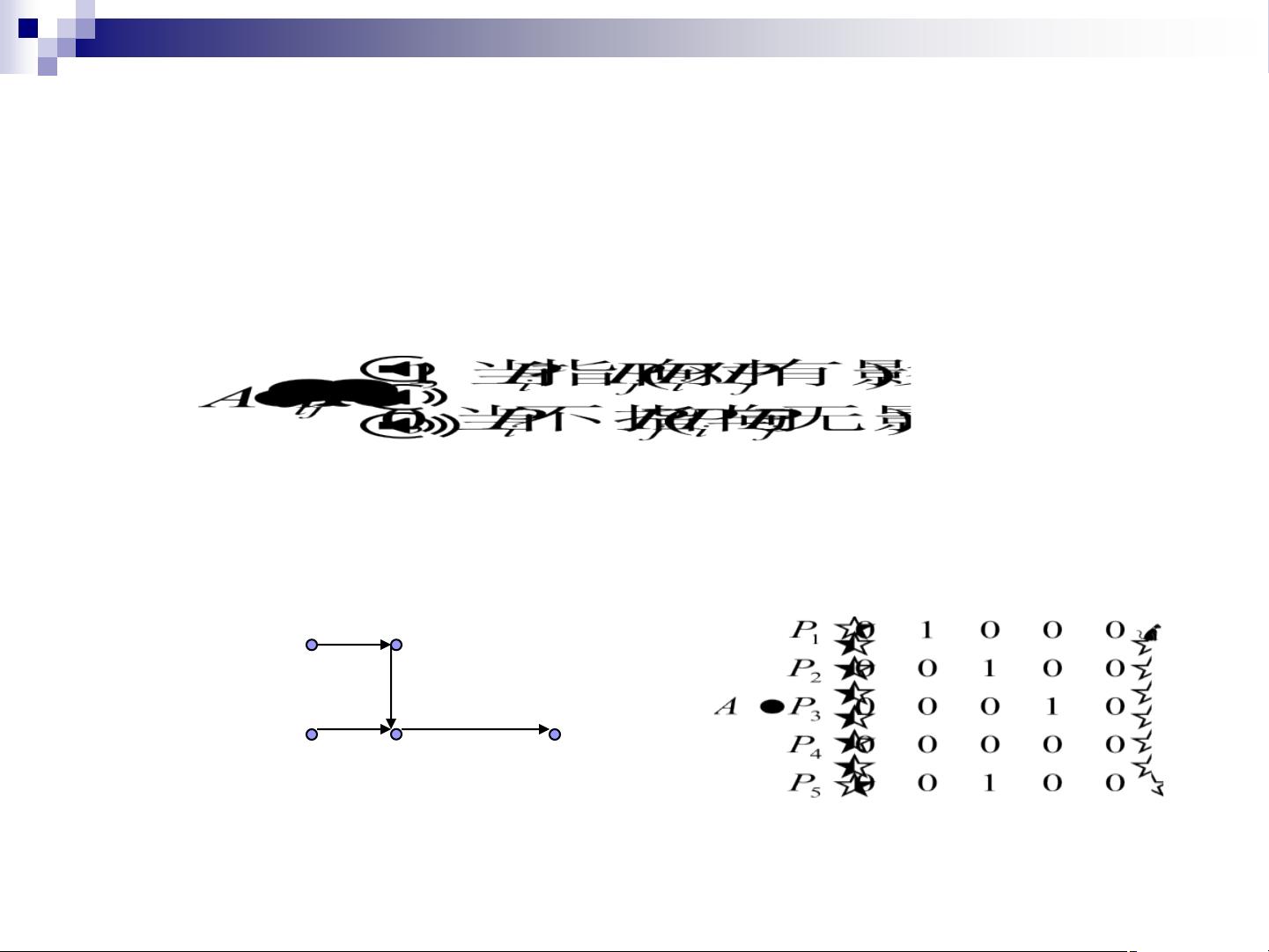
解析结构模型（ISM模型）是一种用于描绘复杂系统中各组件之间相互关系的理论框架，尤其在社会科学、管理科学以及信息技术领域广泛应用。模型的核心是通过有向图和邻接矩阵来表示系统内各单元的相互作用。 有向图是ISM模型的基础，由结点（顶点）和边（支路或弧）组成，其中边的方向（箭头）表示了影响或依赖的方向。例如，在一个能源系统中，哈尔滨可能通过煤炭生产热能，这个关系可以用一个从"煤"到"热能"的有向边来表示。有向图能够直观地展示系统内的因果链。 邻接矩阵是将有向图转换为数值形式的工具，它是一个二维数组，其中的元素aij表示结点Pi对结点Pj是否有直接影响。如果Pi影响Pj，那么aij为1，否则为0。邻接矩阵的特性包括： 1. 全零行对应的结点是汇点，意味着没有其他结点对其有影响，即系统输出。 2. 全零列对应的结点是源点，没有其他结点对其有依赖，即系统输入。 3. 每个点的行中1的数量代表离开该点的影响数。 4. 每个点的列中1的数量表示影响该点的其他结点数。 5. 邻接矩阵的转置AT表示反向的有向图。 可达矩阵是基于邻接矩阵构建的，用于描述系统中两点间是否存在长度不超过n-1的通路。通过迭代计算邻接矩阵的幂，可以得到可达矩阵R。例如，若R中的元素rij为1，表示从Pi可以经过不超过k条边到达Pj。 逻辑关系也可以用来建立可达矩阵，通过中心要素构造法。首先选择系统中的一个要素或子系统作为中心要素Pi，然后找出其上位集L（Pi）（被Pi影响的要素）、下位集D（Pi）（影响Pi的要素）以及无关集V（Pi）（与Pi无关的要素）。由此，可以构建出系统中所有元素间的可达性关系矩阵。 在数学证明方面，如果已知两个矩阵A和B都是可达矩阵，并且存在一个矩阵X，那么根据可达矩阵的性质，可以证明XA+BX=X。这是因为X乘以A或B的结果反映了系统中所有可达路径的组合，而这两个组合相加后，由于可达矩阵的定义，路径会被重复计算一次，从而得出原矩阵X。 ISM模型通过有向图、邻接矩阵和可达矩阵提供了一种系统分析的方法，帮助我们理解复杂系统中各个部分如何相互影响，并可应用于决策支持、系统设计和问题解决等多个领域。