Sequential Minimal Optimization A Fast Algorithm for Training

preview
试读
21页
smo算法
需积分: 0 0 下载量 174 浏览量 更新于2023-03-05 收藏 87KB PDF 举报
Sequential Minimal Optimization (SMO) Algorithm for Training Support Vector Machines SMO 算法是 John C. Platt 于 1998 年提出的一个快速算法，用于训练支持向量机（Support Vector Machines，SVM）。该算法的提出主要是为了解决传统 SVM 训练算法的两个主要问题：计算时间长和内存需求高。 SMO 算法的主要思想是将大型二次规划（Quadratic Programming，QP）问题分解成一系列小型的 QP 问题，每个小型 QP 问题可以通过解析方法解决，从而避免了使用数值优化方法对大型 QP 问题进行求解。这种方法可以显著减少计算时间和内存需求。 SMO 算法的优点包括： 1. 快速计算：SMO 算法可以显著加速 SVM 训练过程，特别是在处理大规模数据集时。 2. 低内存需求：SMO 算法的内存需求与训练集大小呈线性关系，这使得该算法可以处理非常大的训练集。 3. 简单实现：SMO 算法的实现相对简单，易于理解和实现。 SMO 算法的应用前景非常广泛，包括图像识别、自然语言处理、文本分类、生物信息学等领域。 SMO 算法的实现步骤可以概括为以下几个步骤： 1. 数据预处理：对训练数据进行预处理，包括数据 normalization、特征提取等步骤。 2. 初始化：初始化 SVM 模型的参数，包括惩罚参数、kernel 参数等。 3. SMO 算法：使用 SMO 算法来解决 SVM 训练问题，包括将大型 QP 问题分解成小型 QP 问题、解析解决小型 QP 问题、更新 SVM 模型参数等步骤。 4. 模型评估：对训练好的 SVM 模型进行评估，包括计算准确率、召回率、F1 值等指标。 SMO 算法的优点和缺点： 优点： * 快速计算 * 低内存需求 * 简单实现 缺点： * 只适用于训练 SVM 模型 * 对于某些数据集，SMO 算法可能不如其他算法快 SMO 算法是一种快速、简单且高效的 SVM 训练算法，适用于解决大规模 SVM 训练问题。
1
Sequential Minimal Optimization:
A Fast Algorithm for Training Support Vector Machines
John C. Platt
Microsoft Research
jplatt@microsoft.com
Technical Report MSR-TR-98-14
April 21, 1998
© 1998 John Platt
ABSTRACT
This paper proposes a new algorithm for training support vector machines: Sequential
Minimal Optimization, or SMO. Training a support vector machine requires the solution of
a very large quadratic programming (QP) optimization problem. SMO breaks this large
QP problem into a series of smallest possible QP problems. These small QP problems are
solved analytically, which avoids using a time-consuming numerical QP optimization as an
inner loop. The amount of memory required for SMO is linear in the training set size,
which allows SMO to handle very large training sets. Because matrix computation is
avoided, SMO scales somewhere between linear and quadratic in the training set size for
various test problems, while the standard chunking SVM algorithm scales somewhere
between linear and cubic in the training set size. SMO’s computation time is dominated by
SVM evaluation, hence SMO is fastest for linear SVMs and sparse data sets. On real-
world sparse data sets, SMO can be more than 1000 times faster than the chunking
algorithm.
1. INTRODUCTION
In the last few years, there has been a surge of interest in Support Vector Machines (SVMs) [19]
[20] [4]. SVMs have empirically been shown to give good generalization performance on a wide
variety of problems such as handwritten character recognition [12], face detection [15], pedestrian
detection [14], and text categorization [9].
However, the use of SVMs is still limited to a small group of researchers. One possible reason is
that training algorithms for SVMs are slow, especially for large problems. Another explanation is
that SVM training algorithms are complex, subtle, and difficult for an average engineer to
implement.
This paper describes a new SVM learning algorithm that is conceptually simple, easy to
implement, is generally faster, and has better scaling properties for difficult SVM problems than
the standard SVM training algorithm. The new SVM learning algorithm is called Sequential
Minimal Optimization (or SMO). Instead of previous SVM learning algorithms that use
numerical quadratic programming (QP) as an inner loop, SMO uses an analytic QP step.
This paper first provides an overview of SVMs and a review of current SVM training algorithms.
The SMO algorithm is then presented in detail, including the solution to the analytic QP step,
2
heuristics for choosing which variables to optimize in the inner loop, a description of how to set
the threshold of the SVM, some optimizations for special cases, the pseudo-code of the algorithm,
and the relationship of SMO to other algorithms.
SMO has been tested on two real-world data sets and two artificial data sets. This paper presents
the results for timing SMO versus the standard “chunking” algorithm for these data sets and
presents conclusions based on these timings. Finally, there is an appendix that describes the
derivation of the analytic optimization.
1.1 Overview of Support Vector Machines
Vladimir Vapnik invented Support Vector Machines in 1979 [19]. In its simplest, linear form, an
SVM is a hyperplane that separates a set of positive examples from a set of negative examples
with maximum margin (see figure 1). In the linear case, the margin is defined by the distance of
the hyperplane to the nearest of the positive and negative examples. The formula for the output
of a linear SVM is
uwxb=⋅−
rr
, (1)
where w is the normal vector to the hyperplane and x is the input vector. The separating
hyperplane is the plane u=0. The nearest points lie on the planes
u =±1. The margin m is thus
m
w
=
1
2
|| ||
.
(2)
Maximizing margin can be expressed via the following optimization problem [4]:
min || || ( ) , ,
,
r
rrr
wb
ii
wywxbi
1
2
2
1subject to ⋅−≥∀ (3)
Positive Examples
Negative Examples
Maximize distances to nearest
points
Space of possible inputs
Figure 1 A linear Support Vector Machine
3
where x
i
is the ith training example, and y
i
is the correct output of the SVM for the ith training
example. The value y
i
is +1 for the positive examples in a class and –1 for the negative examples.
Using a Lagrangian, this optimization problem can be converted into a dual form which is a QP
problem where the objective function Ψ is solely dependent on a set of Lagrange multipliers α
i
,
min ( ) min ( ) ,
rr
r
rr
αα
αααα
Ψ= ⋅ −
===
∑∑∑
1
2
111
yy x x
i
j
N
i
N
ji j ij i
i
N
(4)
(where N is the number of training examples), subject to the inequality constraints,
α
i
i≥
∀
0, , (5)
and one linear equality constraint,
y
i
i
N
i
=
∑
=
1
0
α
. (6)
There is a one-to-one relationship between each Lagrange multiplier and each training example.
Once the Lagrange multipliers are determined, the normal vector
r
w
and the threshold b can be
derived from the Lagrange multipliers:
rrrr
wyxbwxy
i
i
N
ii k k
==⋅− >
=
∑
1
0
αα
,.for some
k
(7)
Because
r
w
can be computed via equation (7) from the training data before use, the amount of
computation required to evaluate a linear SVM is constant in the number of non-zero support
vectors.
Of course, not all data sets are linearly separable. There may be no hyperplane that splits the
positive examples from the negative examples. In the formulation above, the non-separable case
would correspond to an infinite solution. However, in 1995, Cortes & Vapnik [7] suggested a
modification to the original optimization statement (3) which allows, but penalizes, the failure of
an example to reach the correct margin. That modification is:
min || || ( ) , ,
,,
r
r
rrr
wb
i
i
N
ii i
wC ywxb i
ξ
ξξ
1
2
2
1
1+⋅−≥−∀
=
∑
subject to (8)
where ξ
i
are slack variables that permit margin failure and C is a parameter which trades off wide
margin with a small number of margin failures. When this new optimization problem is
transformed into the dual form, it simply changes the constraint (5) into a box constraint:
0 ≤≤∀
α
i
C
i,. (9)
The variables ξ
i
do not appear in the dual formulation at all.
SVMs can be even further generalized to non-linear classifiers [2]. The output of a non-linear
SVM is explicitly computed from the Lagrange multipliers:
4
uyKxxb
j
j
N
jj
=−
=
∑
1
α
(,) ,
rr
(10)
where K is a kernel function that measures the similarity or distance between the input vector
r
x
and the stored training vector
r
x
j
. Examples of K include Gaussians, polynomials, and neural
network non-linearities [4]. If K is linear, then the equation for the linear SVM (1) is recovered.
The Lagrange multipliers α
i
are still computed via a quadratic program. The non-linearities alter
the quadratic form, but the dual objective function Ψ is still quadratic in α:
min ( ) min ( , ) ,
,,
.
rr
r
rr
αα
αααα
α
α
Ψ= −
≤≤∀
=
===
=
∑∑∑
∑
1
2
111
1
0
0
yyK x x
Ci
y
ij i j i j
j
N
i
N
i
i
N
i
ii
i
N
(11)
The QP problem in equation (11), above, is the QP problem that the SMO algorithm will solve.
In order to make the QP problem above be positive definite, the kernel function K must obey
Mercer’s conditions [4].
The Karush-Kuhn-Tucker (KKT) conditions are necessary and sufficient conditions for an
optimal point of a positive definite QP problem. The KKT conditions for the QP problem (11)
are particularly simple. The QP problem is solved when, for all i:
α
α
α
iii
iii
iii
yu
Cyu
Cyu
=⇔ ≥
<<⇔ =
=⇔ ≤
01
01
1
,
,
.
(12)
where u
i
is the output of the SVM for the ith training example. Notice that the KKT conditions
can be evaluated on one example at a time, which will be useful in the construction of the SMO
algorithm.
1.2 Previous Methods for Training Support Vector Machines
Due to its immense size, the QP problem (11) that arises from SVMs cannot be easily solved via
standard QP techniques. The quadratic form in (11) involves a matrix that has a number of
elements equal to the square of the number of training examples. This matrix cannot be fit into
128 Megabytes if there are more than 4000 training examples.
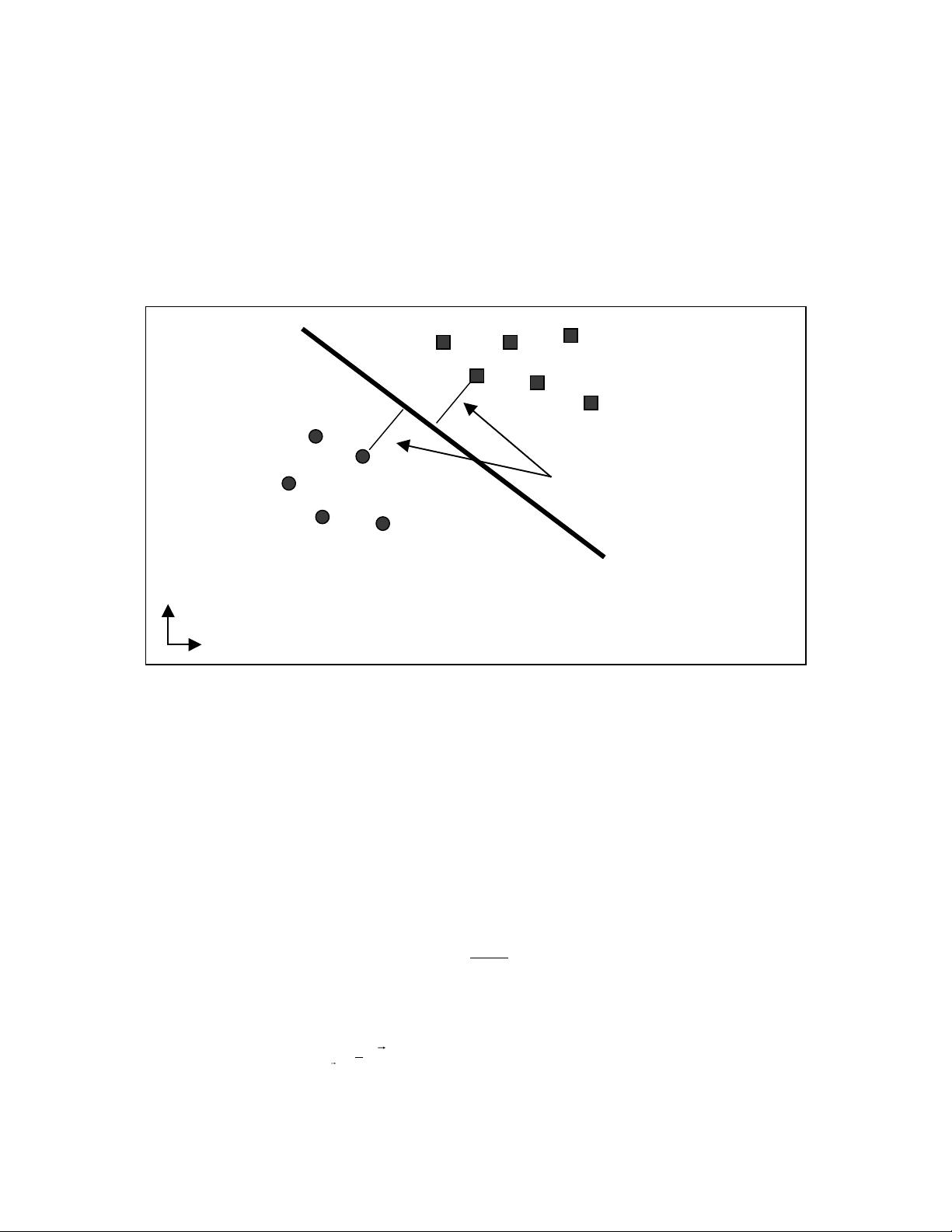
Vapnik [19] describes a method to solve the SVM QP, which has since been known as
“chunking.” The chunking algorithm uses the fact that the value of the quadratic form is the same
if you remove the rows and columns of the matrix that corresponds to zero Lagrange multipliers.
Therefore, the large QP problem can be broken down into a series of smaller QP problems, whose
ultimate goal is to identify all of the non-zero Lagrange multipliers and discard all of the zero
Lagrange multipliers. At every step, chunking solves a QP problem that consists of the following
examples: every non-zero Lagrange multiplier from the last step, and the M worst examples that
violate the KKT conditions (12) [4], for some value of M (see figure 2). If there are fewer than M
examples that violate the KKT conditions at a step, all of the violating examples are added in.
Each QP sub-problem is initialized with the results of the previous sub-problem. At the last step,

剩余20页未读，继续阅读

资源推荐
资源评论
楼兰小石头
  • 粉丝: 118
  • 资源: 15
上传资源 快速赚钱
voice
center-task 前往需求广场，查看用户热搜

最新资源