第3章 第3节 堆及其应用(C++版).ppt

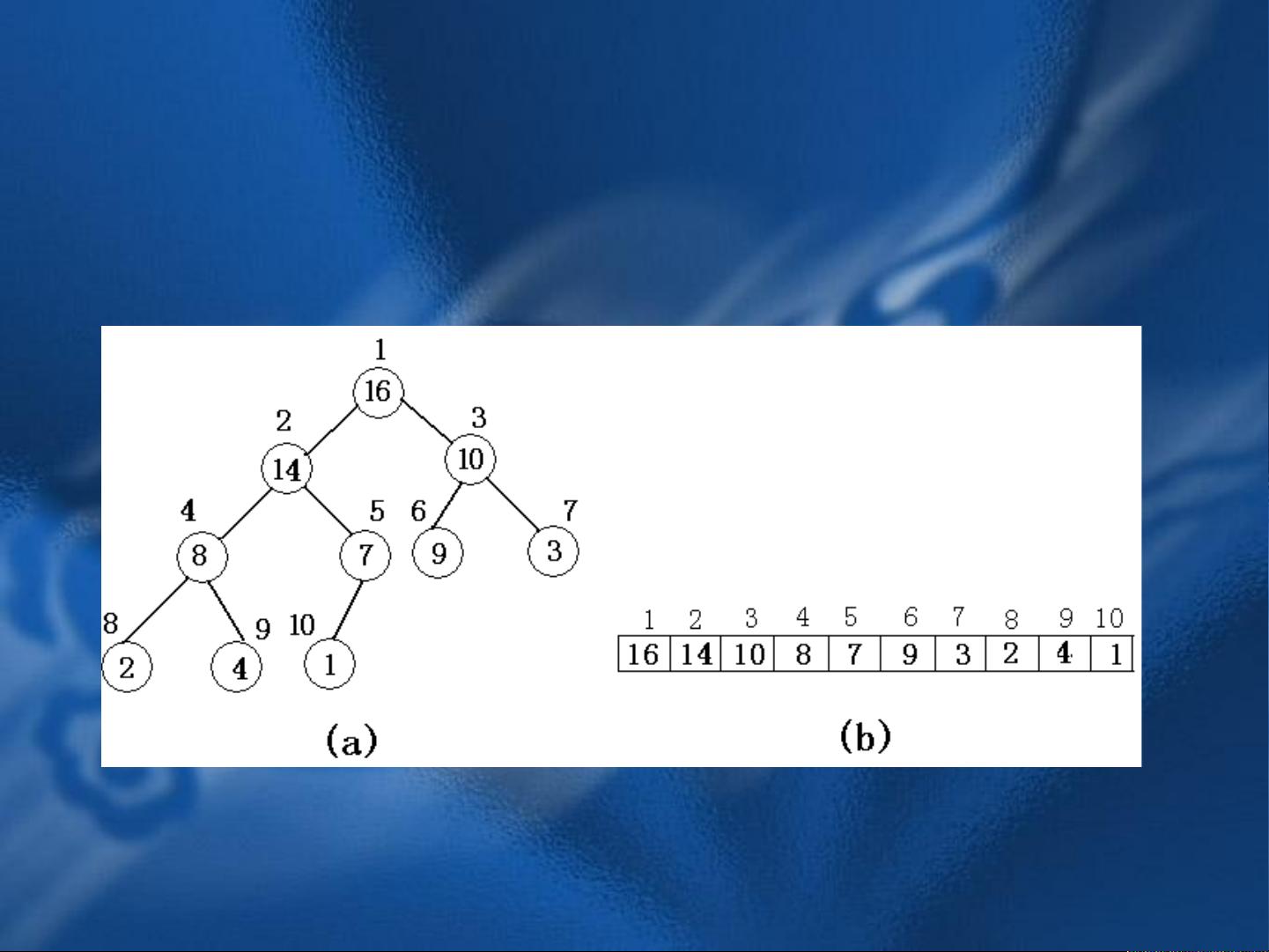
标题中的“第3章 第3节 堆及其应用(C++版).ppt”指的是一个关于数据结构中的堆的讲解，特别关注C++实现。描述中没有提供额外信息，但标签明确指出了“数据结构”，表明内容将围绕数据结构的堆进行讨论。 在数据结构中，堆是一种特殊的树形数据结构，它同时具备数组的特性。**完全二叉树**是堆的基础概念，它是一种深度为K的二叉树，除了最后一层外，所有层的节点都完全填充，且最后一层的节点尽可能地靠左。这意味着在数组中表示完全二叉树时，每个节点的位置与其在树中的位置相对应。 **堆的定义**是基于完全二叉树的数组表示。堆中的每个元素都有一个对应的数组索引，根节点位于索引1的位置，而其他节点可以通过父节点（index/2）、左孩子（2*index）和右孩子（2*index + 1）的计算公式找到。堆有两种主要类型：**大根堆**和**小根堆**。在大根堆中，除了根节点之外，每个节点的值都不大于其父节点的值，因此根节点始终存储最大值。相反，小根堆则确保每个节点的值不小于其父节点的值，根节点是最小值。 **堆的操作**主要包括**put操作**和**get操作**。put操作用于向堆中添加元素，这通常涉及将新元素添加到数组的末尾，然后自下而上地调整以保持堆的性质。在C++中，可以使用STL中的`push_heap`函数实现这个操作，对于小根堆，需要传递一个比较器`greater<int>`来保证插入的元素被放置在正确的位置。get操作则是从堆中移除并返回最大（或最小）元素。这个操作涉及到替换根节点为末尾元素，减小堆的大小，然后自上而下地调整以恢复堆的性质。在C++中，可以使用`pop_heap`函数完成这一过程。 通过put和get操作，可以构建和维护堆结构，使得堆常用于优先队列、排序算法（如堆排序）以及其他需要快速访问最大或最小元素的场景。堆的效率主要在于其O(log n)的时间复杂度，这是由于其树形结构和局部调整的特性。 堆是数据结构中非常重要的一个概念，尤其在处理需要高效查找最大或最小元素的问题时。C++提供了方便的STL工具来实现堆的操作，简化了编程过程。理解和掌握堆的性质以及如何通过put和get操作维护堆的结构，对于任何深入学习数据结构和算法的人来说都是至关重要的。