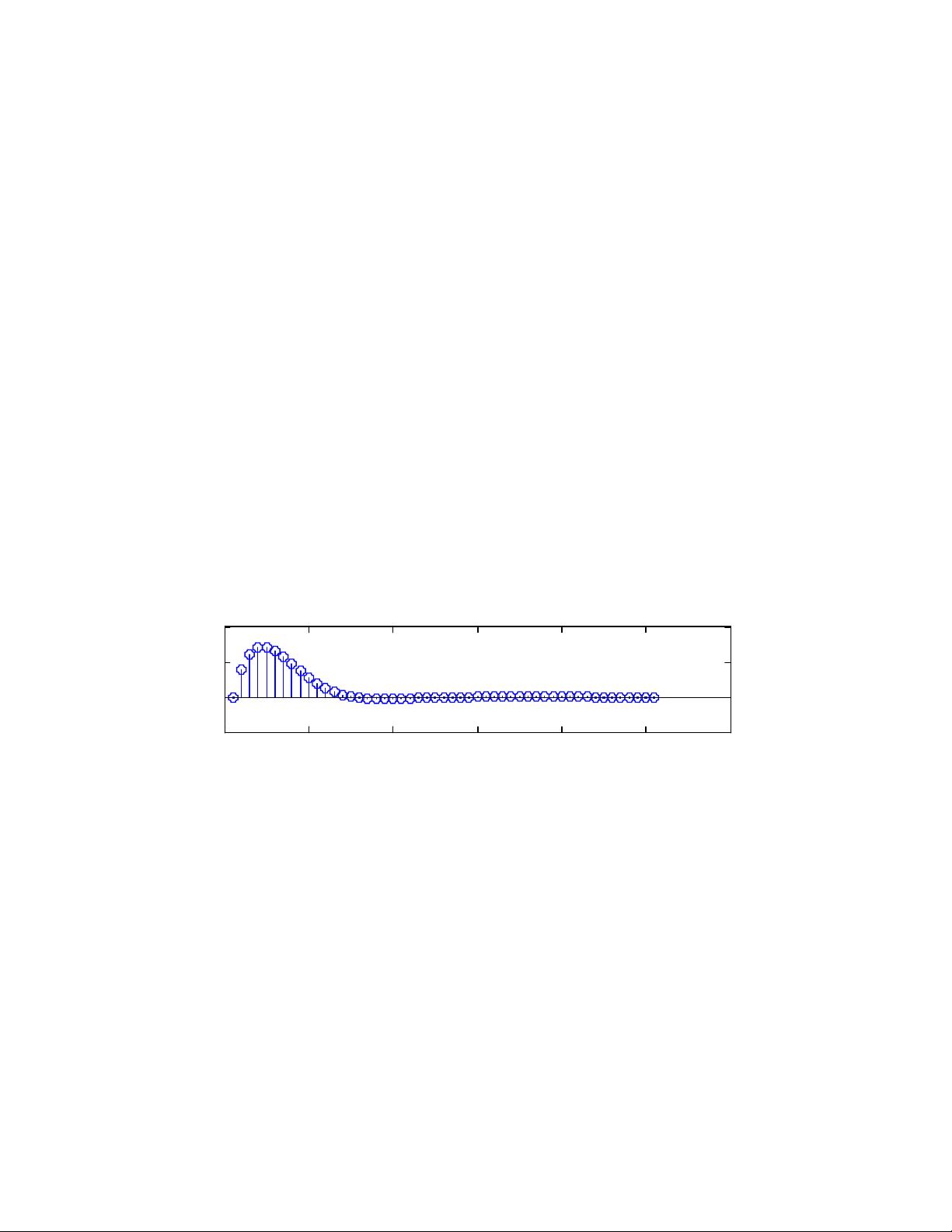
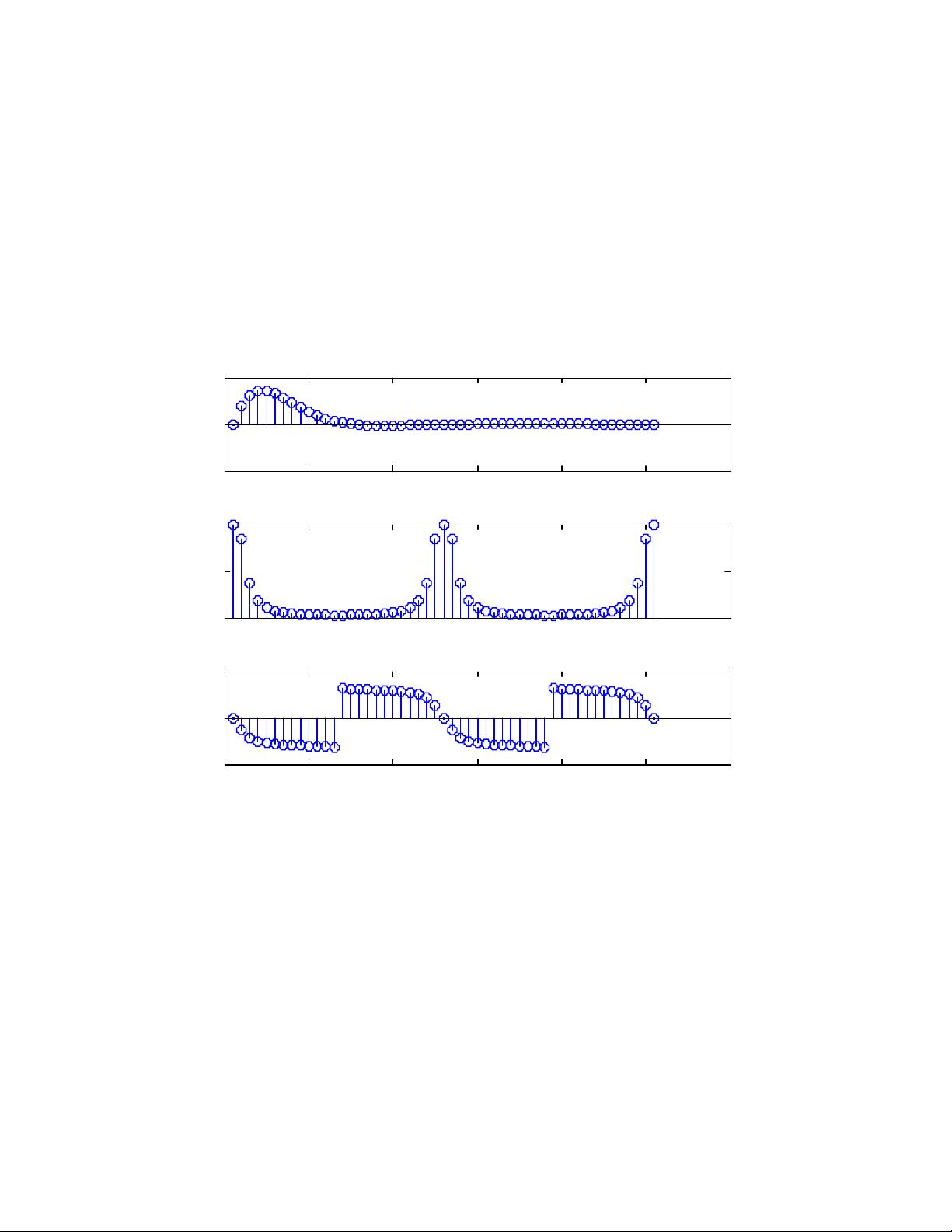
### MATLAB下的数字信号处理实现示例
#### 一、理想采样信号序列
在本示例中，我们探讨了如何在MATLAB环境下生成并分析理想采样的信号序列。理想采样信号序列通常指的是通过采样连续时间信号得到的离散时间信号。
##### 1.1 信号生成
我们需要生成一个理想的采样信号序列`x(n)`。在这个例子中，我们定义了一个长度为50的序列，并设定了相关的参数：
- `n = 0:50`: 序列的长度。
- `A = 444.128`: 信号的振幅。
- `a = 50 * sqrt(2.0) * pi`: 衰减系数。
- `T = 0.001`: 采样间隔。
- `w0 = 50 * sqrt(2.0) * pi`: 角频率。
信号`x(n)`由以下公式给出：
\[ x(n) = A \cdot e^{-anT} \cdot \sin(w_0 n T) \]
其中`.*`表示元素级别的乘法操作，这在MATLAB中用于对向量或矩阵执行逐元素运算。
```matlab
n = 0:50;
A = 444.128;
a = 50 * sqrt(2.0) * pi;
T = 0.001;
w0 = 50 * sqrt(2.0) * pi;
x = A * exp(-a * n * T) .* sin(w0 * n * T);
```
接着，我们清除已有的图形并绘制信号`x(n)`：
```matlab
close all;
subplot(3, 1, 1);
stem(x);
title('理想采样信号序列');
```
##### 1.2 信号频谱分析
接下来，我们分析该信号的幅度谱和相位谱。为此，我们定义了一个频率向量`W`，计算了信号`x(n)`的离散傅里叶变换，并绘制了幅度谱和相位谱。
- 定义频率向量`W`：
```matlab
k = -25:25;
W = (pi / 12.5) * k;
```
- 计算离散傅里叶变换`X`：
```matlab
X = x * (exp(-j * pi / 12.5)).^(n' * k);
```
- 绘制幅度谱和相位谱：
```matlab
magX = abs(X);
subplot(3, 1, 2);
stem(magX);
title('理想采样信号序列的幅度谱');
angX = angle(X);
subplot(3, 1, 3);
stem(angX);
title('理想采样信号序列的相位谱');
```
#### 二、参数变化的影响
为了观察不同参数对信号的影响，我们将采样间隔`T`改为1，角频率`Ω`改为2.0734，衰减系数`a`改为0.4，振幅`A`改为1。然后重新生成信号`x(n)`，并重复上述的信号分析步骤。这个过程有助于理解参数变化对信号形态及频谱特征的影响。
```matlab
n = 0:50;
A = 1;
a = 0.4;
T = 1;
w0 = 2.0734;
x = A * exp(-a * n * T) .* sin(w0 * n * T);
close all;
subplot(3, 1, 1);
stem(x);
title('理想采样信号序列');
k = -25:25;
W = (pi / 12.5) * k;
X = x * (exp(-j * pi / 12.5)).^(n' * k);
magX = abs(X);
subplot(3, 1, 2);
stem(magX);
title('理想采样信号序列的幅度谱');
angX = angle(X);
subplot(3, 1, 3);
stem(angX);
title('理想采样信号序列的相位谱');
```
#### 三、单位脉冲序列与特定冲击串
##### 3.1 单位脉冲序列
单位脉冲序列是数字信号处理中的基本序列之一，它在MATLAB中可以通过使用`zeros`函数来创建。下面展示了如何生成一个长度为50的单位脉冲序列，并绘制其图形以及幅度谱和相位谱。
```matlab
n = 1:50;
x = zeros(1, 50);
x(1) = 1;
close all;
subplot(3, 1, 1);
stem(x);
title('单位冲击信号序列');
k = -25:25;
X = x * (exp(-j * pi / 12.5)).^(n' * k);
magX = abs(X);
subplot(3, 1, 2);
stem(magX);
title('单位冲击信号的幅度谱');
angX = angle(X);
subplot(3, 1, 3);
stem(angX);
title('单位冲击信号的相位谱');
```
##### 3.2 特定冲击串
特定冲击串是指具有特定形状的脉冲序列。例如，在本示例中，我们创建了一个长度为50的序列，其中前四个元素分别为1, 2.5, 2.5, 1。这个序列同样可以通过`zeros`函数结合元素赋值的方式创建。我们绘制了该序列及其频谱。
```matlab
n = 1:50;
x = zeros(1, 50);
x(1) = 1;
x(2) = 2.5;
x(3) = 2.5;
x(4) = 1;
close all;
subplot(3, 1, 1);
stem(x);
title('特定冲击信号序列');
k = -25:25;
X = x * (exp(-j * pi / 12.5)).^(n' * k);
magX = abs(X);
subplot(3, 1, 2);
stem(magX);
title('特定冲击信号的幅度谱');
angX = angle(X);
subplot(3, 1, 3);
stem(angX);
title('特定冲击信号的相位谱');
```
#### 四、卷积
卷积是数字信号处理中一个重要的概念，它可以用来表示两个信号相互作用的效果。在MATLAB中，可以使用内置的`conv`函数来进行卷积运算。下面展示了一个简单的卷积示例：
```matlab
n = 1:50;
hb = zeros(1, 50);
hb(1) = 1;
hb(2) = 2.5;
hb(3) = 2.5;
hb(4) = 1;
close all;
subplot(3, 1, 1);
stem(hb);
title('系统hb[n]');
m = 1:50;
A = 444.128;
a = 50 * sqrt(2.0) * pi;
T = 0.001;
w0 = 50 * sqrt(2.0) * pi;
x = A * exp(-a * m * T) .* sin(w0 * m * T);
y = conv(x, hb);
```
通过这些示例，我们可以更深入地理解数字信号处理的基本概念和技术，特别是在MATLAB这样的工具中进行信号分析和处理的方法。
