《算法导论》完整的课件下载
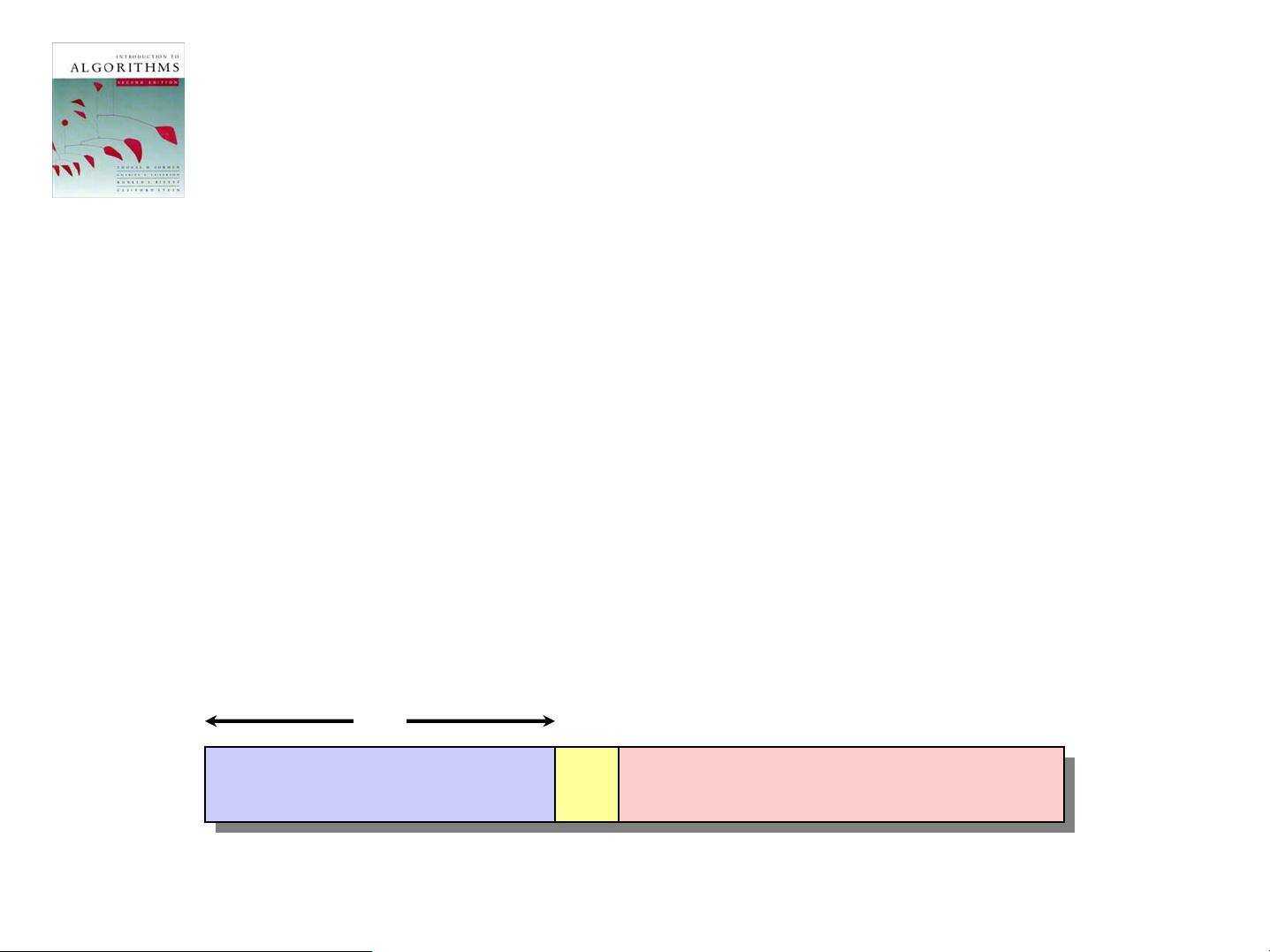
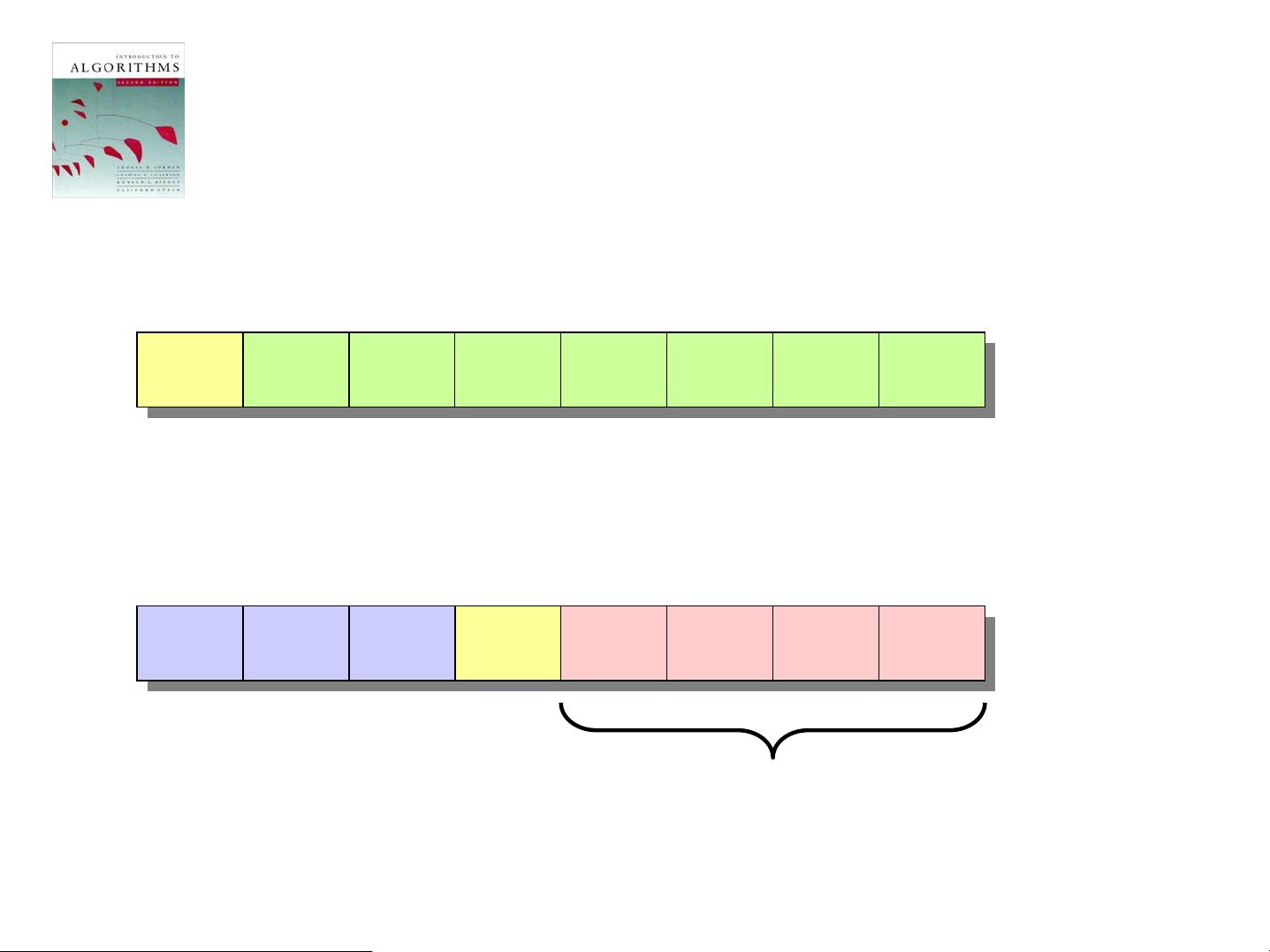
### 《算法导论》中的顺序统计量算法详解 #### 一、算法概述与背景介绍 《算法导论》是一本经典的计算机科学教材,由Thomas H. Cormen、Charles E. Leiserson、Ronald L. Rivest和Clifford Stein共同编写。该书涵盖了广泛的算法设计与分析技术,是学习算法的基础读物。本次讨论的重点在于书中提到的顺序统计量(Order Statistics)算法,这是一种找出数组中第i小元素的有效方法。 #### 二、顺序统计量算法介绍 ##### 1. 基本概念 顺序统计量问题指的是在未排序数组中找到第i小的元素,即找到具有第i个秩的元素。例如: - 当i = 1时,即寻找最小值; - 当i = n时,即寻找最大值; - 当i = ⌊(n + 1) / 2⌋ 或 ⌈(n + 1) / 2⌉ 时,即寻找中位数。 ##### 2. 常规算法 最简单的方法是先对数组进行排序,然后返回索引为i的元素。这种方法的时间复杂度为O(n log n),使用归并排序或堆排序可以达到这个时间复杂度,而快速排序在最坏情况下可能无法达到。 #### 三、随机化分治算法 为了提高效率,《算法导论》提出了一个基于随机化分治策略的算法——`RAND-SELECT`。 ##### 1. 算法描述 - 如果数组大小为1,则直接返回该元素。 - 使用随机分区函数将数组分为两部分:小于等于枢轴的部分和大于枢轴的部分。 - 计算枢轴的秩,并根据目标秩与枢轴秩的关系递归地处理相应子数组。 ```plaintext RAND-SELECT(A, p, q, i) if p = q then return A[p] r ← RAND-PARTITION(A, p, q) k ← r - p + 1 if i = k then return A[r] if i < k then return RAND-SELECT(A, p, r - 1, i) else return RAND-SELECT(A, r + 1, q, i - k) ``` ##### 2. 示例 假设我们需要找到数组`[2, 5, 3, 6, 8, 10, 13, 11]`中第7小的元素。 - 首次调用`RAND-SELECT`后,假设随机选择的枢轴是10,那么数组被划分为`[2, 5, 3, 6, 8]`和`[13, 11]`两部分,枢轴10的秩为4。 - 因为第7小的元素位于左侧子数组中,所以接下来在左侧子数组中递归地调用`RAND-SELECT`。 - 最终通过多次递归调用找到第7小的元素为8。 #### 四、算法分析 ##### 1. 平均情况分析 为了分析`RAND-SELECT`算法的平均情况运行时间,我们定义T(n)为输入规模为n时的期望运行时间。设Xk为指示随机变量,当PARTITION函数产生k:n-k-1的分割时取值为1,否则为0。 - **幸运情况**:如果分割大致均衡,那么运行时间主要取决于递归调用的深度,此时算法的期望运行时间为O(n)。 - **不幸情况**:如果总是得到最差分割,即每次都是n-1的分割,那么算法退化为O(n^2),比排序还要慢。 ##### 2. 随机化分析 对于每个可能的k值(0到n-1),我们可以计算其出现的概率,进而计算出T(n)的期望值。具体而言,我们可以利用线性代数和概率理论来推导出T(n)的期望表达式,证明其为O(n)。 #### 五、总结 《算法导论》中的顺序统计量算法通过随机化分治策略解决了传统排序方法在查找顺序统计量时效率低下的问题。通过合理的随机化,可以在期望时间内达到线性时间复杂度,从而提高了算法的效率。这一算法不仅在理论上具有重要意义,在实际应用中也有着广泛的应用前景。



剩余29页未读,继续阅读

- 粉丝: 9
- 资源: 56
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功