《算法导论》完整的课件下载
### 《算法导论》完整课件下载:关键知识点概览 #### 一、课程介绍与目标 《算法导论》是一本经典的计算机科学教材,它涵盖了算法设计和分析的基础知识,适合计算机科学专业的学生以及对算法感兴趣的自学者。这份课件提供了完整的教学资料,从最基础的概念出发,帮助学习者逐步建立起对算法的理解。 #### 二、排序算法的下界分析:决策树方法 ##### 决策树的概念 决策树是一种用于分析基于比较的排序算法效率的方法。它通过构建一棵树形结构来表示所有可能的比较序列及其结果,从而推导出任何基于比较的排序算法的时间复杂度下限。 **决策树节点**: - 内部节点代表一次元素之间的比较操作。 - 叶子节点代表一个具体的排序结果。 **决策树示例**: - 假设我们有三个元素 \(a_1, a_2, a_3\) 需要进行排序。 - 每个内部节点被标记为 \(i:j\)(其中 \(i, j \in \{1, 2, 3\}\)),表示将对 \(a_i\) 和 \(a_j\) 进行比较。 - 如果 \(a_i \leq a_j\),则沿着该节点的左子树继续进行比较;如果 \(a_i > a_j\),则沿着右子树进行比较。 - 最终达到的叶子节点代表了一种可能的排序结果。 ##### 排序算法的下界证明 决策树提供了一种理论上的证明,表明任何基于比较的排序算法在最坏情况下的时间复杂度至少为 \(O(n \log n)\)。 **证明思路**: - 对于 \(n\) 个不同的元素,存在 \(n!\) 种不同的排序结果。 - 每种排序结果对应于决策树的一个叶子节点。 - 因此,决策树必须至少有 \(n!\) 个叶子节点。 - 要使一棵决策树具有至少 \(n!\) 个叶子节点,其高度至少为 \(\log_2(n!)\)。 - 利用斯特林公式可以证明 \(\log_2(n!) = \Omega(n \log n)\)。 - 因此,任何基于比较的排序算法在最坏情况下的时间复杂度至少为 \(O(n \log n)\)。 #### 三、线性时间排序算法 ##### 计数排序 计数排序是一种适用于一定范围内的整数排序算法。它不是基于比较的排序算法,因此不受 \(O(n \log n)\) 的限制。 **基本思想**: - 创建一个大小等于输入数据范围的计数数组。 - 遍历输入数组,统计每个值出现的次数。 - 根据计数数组中的信息,构建已排序的输出数组。 **时间复杂度**: - 最佳、平均和最坏情况下均为 \(O(n + k)\),其中 \(k\) 是输入数据的最大值与最小值之差。 ##### 基数排序 基数排序是另一种线性时间排序算法,适用于整数或字符串等具有固定位数的数据类型。 **基本思想**: - 从最低有效位开始,依次按照每一位的值进行排序。 - 使用稳定的排序算法(如计数排序)来处理每一位。 **时间复杂度**: - 最佳、平均和最坏情况下均为 \(O(d(n + k))\),其中 \(d\) 表示数字的最大位数,\(k\) 是基数。 #### 四、附录:穿孔卡片 在计算机早期阶段,穿孔卡片是一种常用的数据存储方式。虽然现在已经被淘汰,但在理解早期计算机系统的工作原理时仍有一定的参考价值。 ### 总结 通过《算法导论》的学习,我们可以了解到不同类型的排序算法及其性能特点。决策树方法为我们提供了一种强有力的工具来分析和理解基于比较的排序算法的理论下限。同时,非比较型的排序算法(如计数排序和基数排序)在特定条件下可以实现更高效的排序效果。这些知识对于深入理解算法的设计与分析至关重要。


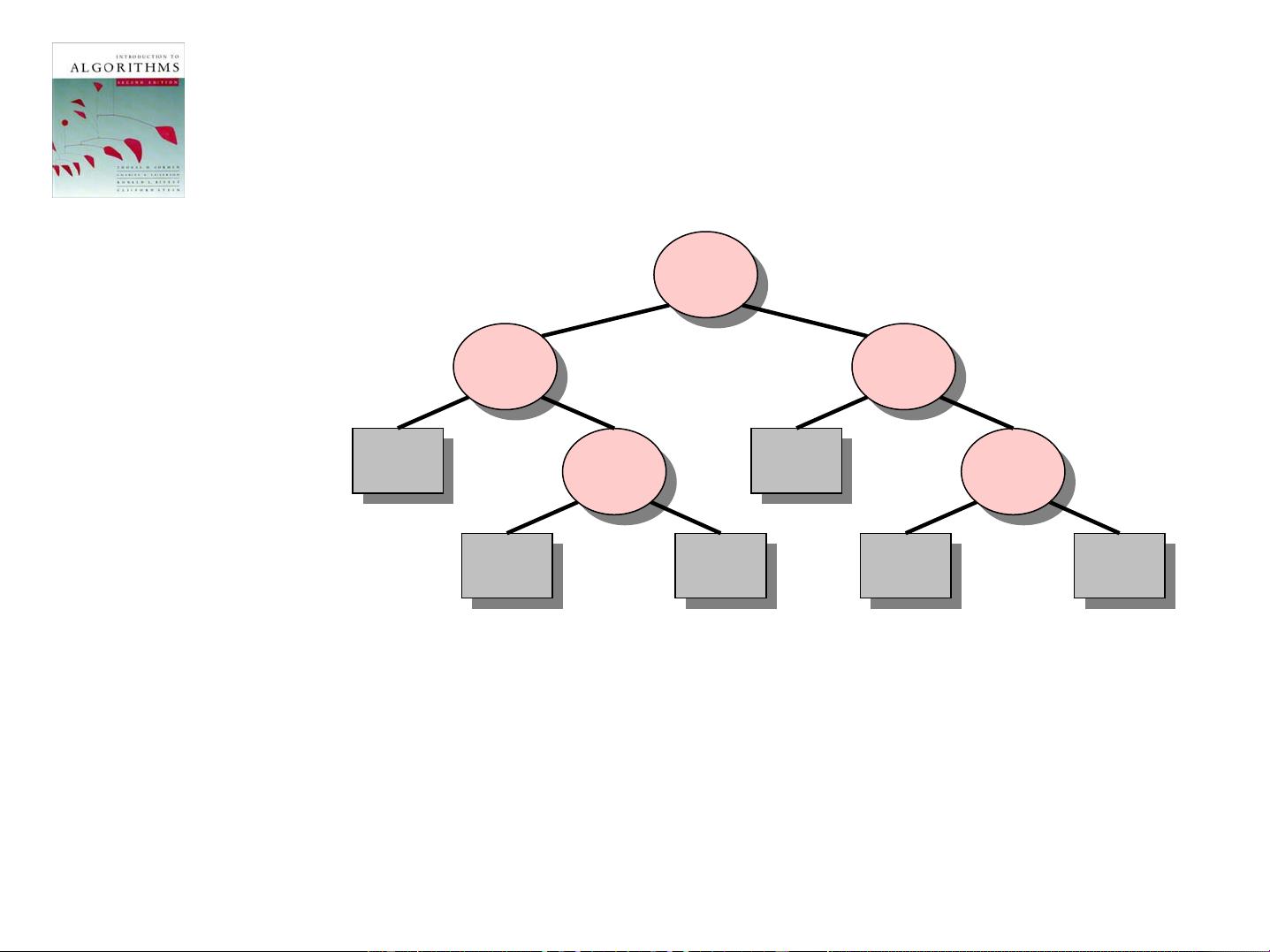
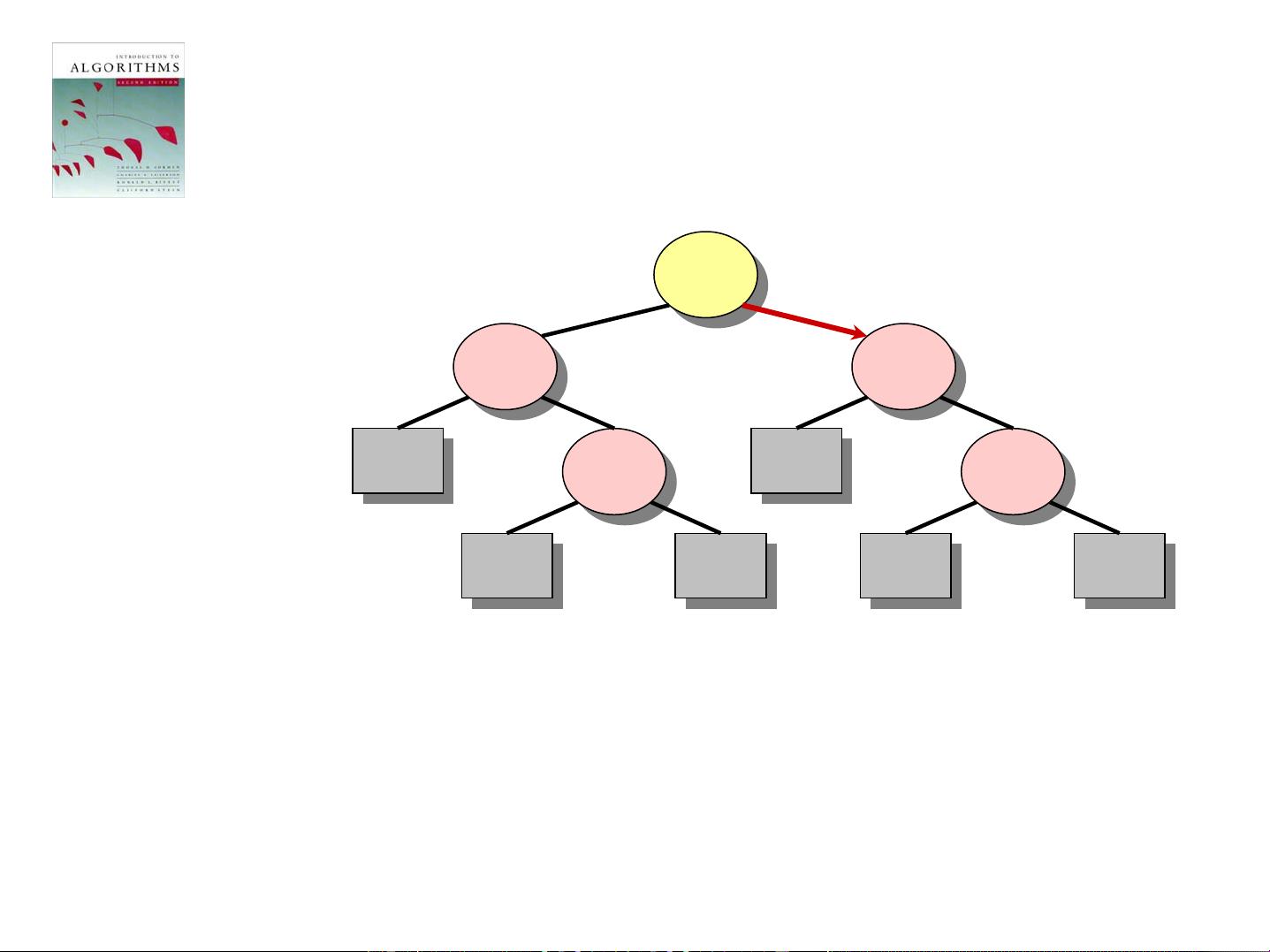
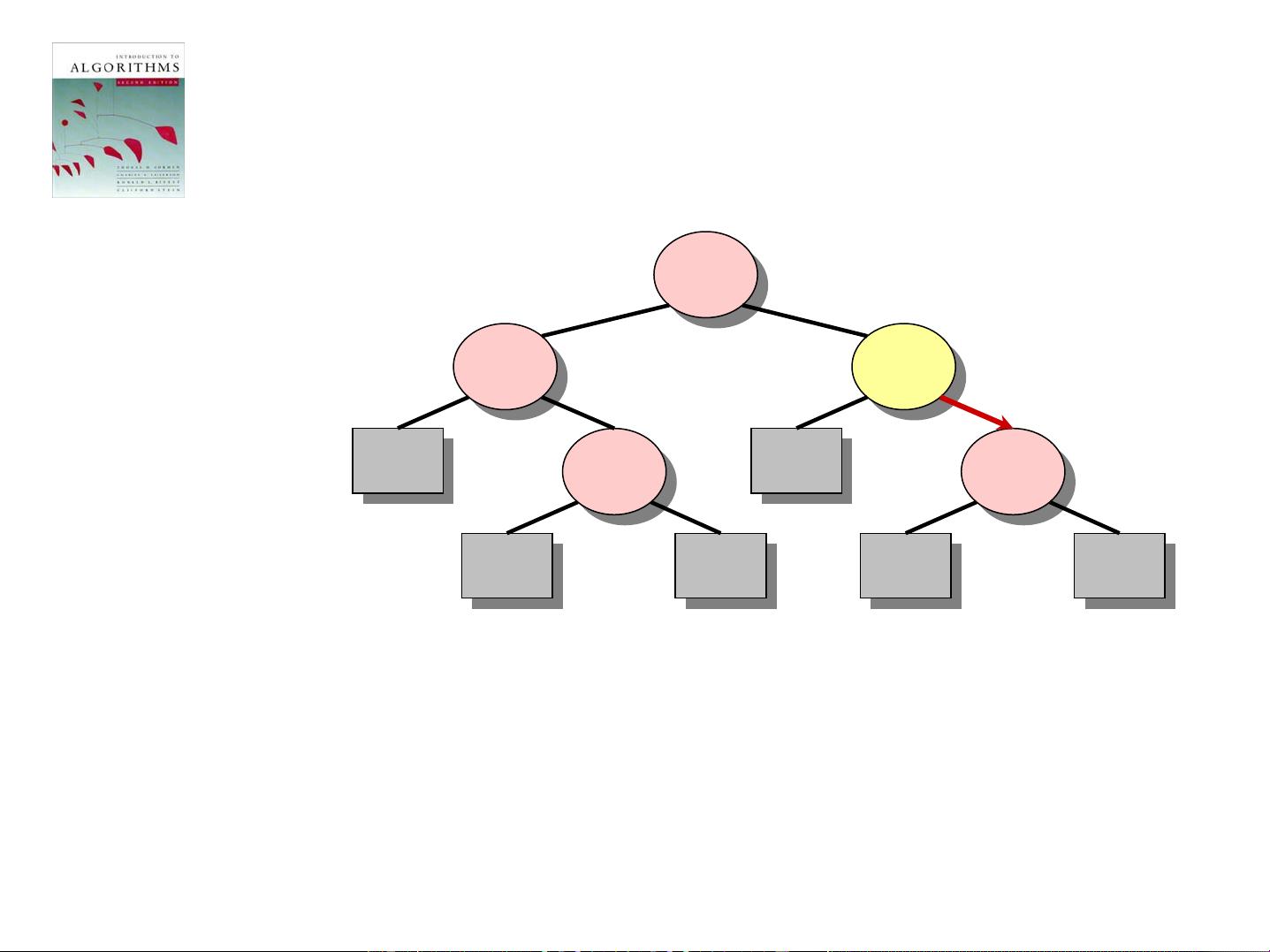
剩余40页未读,继续阅读

- 粉丝: 9
- 资源: 56
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功