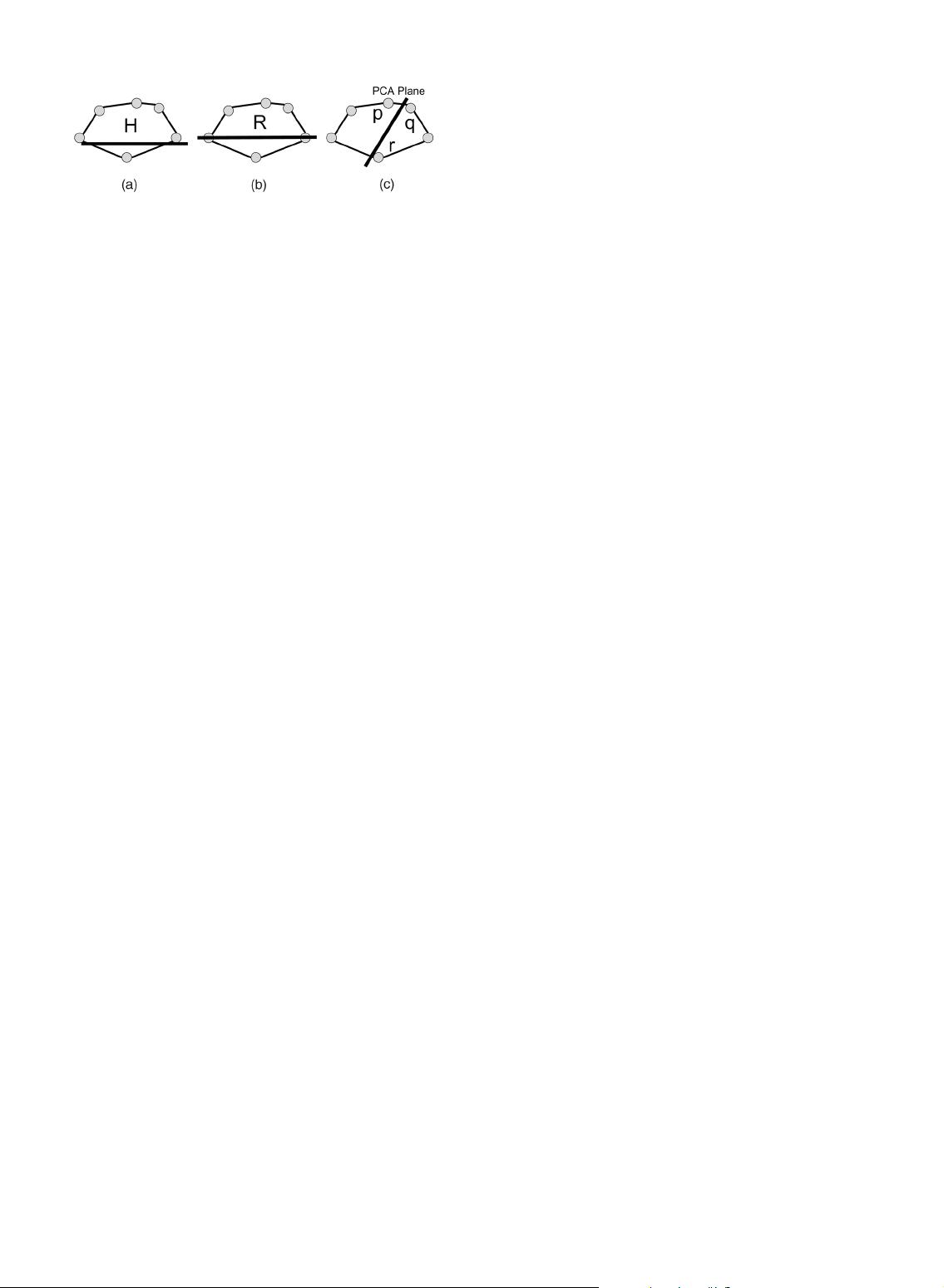kernel contains only low-frequency components, they
deduce that the first nine (low frequency) spherical
harmonics capture more than 99 percent of the reflected
energy. Using this nine-dimensional harmonic plane, a
straightforward face recognition scheme can be developed,
and results obtained in [2] are excellent. Recently Rama-
moorthi [13] developed a novel method based on spherical
harmonics to analytically compute low-dimensional (less
than nine-dimensional) linear approximations to illumina-
tion cones. His results give a theoretical explanation to many
empirical results obtained earlier, e.g., [5].
For face recognition, one way to interpret Basri and
Jacobs’ result is that, for each of the more than six billion
human faces in the world, there exist nine “universal
virtual” lighting conditions such that the nine “harmonic
images” taken for each individual under these conditions
are sufficient to approximate his/her illumination cone
with the harmonic subspace H spanned by these images.
These nine “harmonic lights” are not real lighting condi-
tions because, for some directions, the intensity is negative,
as specified by the spherical harmonic functions. Similarly,
the nine “harmonic images” (basis images) are not real
images because some of the pixel values (image irradiance)
are negative. Therefore, these images must be the result of
some computation from real images or rendered from a
geometric model of a head under synthetic harmon ic
lighting. This requires knowledge of the object’s surface
normals and albedos before the harmonic subspace can be
computed. On the other hand, simple linear algebra tells us
that any set of nine linearly independent vectors (or images)
in H is sufficient to recover the plane. This hints at the
possibility of an easier way to obtain the linear subspace,
that is, can we find a set of nine real images such that the
linear subspace spanned by them coincides with the
harmonic subspace? For all practical purposes, the answer
to this question is “no.” Any real image in H requires the
lighting over the sphere of directions to be a smooth
function specified by a linear combination of the first nine
spherical harmonics, and it would be very difficult to
physically construct such lighting conditions in a common
laboratory or application environment. However, one can
ask a different but related question: Is there another
nine-dimensional linear subspace R that can also provide
a good representation for face recognition? Can R be
constructed in some canonical fashion, perhaps with nine
physically and easily realized lighting conditions?
In this paper, we formulate the problem as follows: We
will consider only single distant and isotropic light sources.
Each such light source can be associated with a point on the
unit sphere s 2 S
2
indicating its direction. Let denote a
subset of the unit sphere S
2
. The problem we wish to solve
is the following: Given and a small integer d (typically
nine or less), find a subset fs
1
; ;s
d
g of such that the
d corresponding lighting directions fl
s
1
; ;l
s
d
g and the
associated d-dimensional subspace R generated by d images
taken under these lighting conditions are a good approx-
imation to the illumination cones of a collection of human
faces. For computational reasons, the set is always
assumed to have finite size and, in this paper, is either
a uniformly sample d sphere or a uniformly sam pled
hemisphere.
Since we know that the harmonic subspace H is a good
representation for face recognition under variable lighting,
it seems reasonable to find a plane R close to H. To make
this notion precise, we need a notion of distance between
two planes. In our first algorithm, the distance between two
planes (not necessarily of the same dimension) is defined to
be the square-sum of the cosines of the principal angles
between them. R is then defined as the plane that has the
smallest distance to H. From the recognition standpoint, it
is also preferable to require that the intersection between R
and the illumination cone C be as large as possible. This
condition is incorporated into our second algorithm. That is,
we want to find a k-dimensional linear subspace R, with k
ranging from 1 to 9, generated by elements in such that
the distance between R and H is minimized (in some way)
while the (unit)-volume R \ C is maximized. In Section 3,
we formulate both algorithms in terms of maximizing an
objective function defined over . Our end result is a set of
k directions (points) in , and R is spanned by the images
taken under the lighting conditions specified by these
k directions.
It turns out that the resulting k light source directions are
qualitatively very similar for different individuals. By
averaging the objective functions for different individuals
and maximizing this new objective function, we obtain a
sequence of configurations of light source directions, called
the universal configurations, such that, on average, the
linear spaces spanned by the corresponding images are a
good approximation to the corresponding illumination
cones. We demonstrate that, by using these universal
configurations, g ood face recognition results can be
obtained. In some cases, as few as five training images
per person are sufficient to produce reasonably accurate
face recognition results if a small error rate can be tolerated.
The main contribution of this paper is the demonstration,
both theoretically and empirically, that it is possible to
employ just a few real images (taken under single distant
and isotropic light sources) to model the various illumina-
tion effects on human faces, provided that the light source
locations are chosen carefully. From a practical standpoint,
acquiring images under a single distant and isotropic light
source is much easier and less costly than alternatives. That
is, the linear subspace R is lot easier to obtain than either the
harmonic subspace H or the illumination cone C. This is
particularly appropriate for acquiring training images of
individuals in a controlled environment such as a driver’s
license office, a bank, or a security office.
This paper is organized as follows: In Section 2, we
briefly summarize the idea of [2] using a harmonic subspace
H for face recognition. The relationship between H and the
illumination cone [3] is explained. Our algorithms for
computing R and the universal configuration are detailed in
Section 3, and Section 4 presents experimental results. The
final section contains a brief summary and conclusion of
this paper. Preliminary results on this topic were presented
in [10], [11]. Some notation used in this paper is listed in
Table 1.
2 IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 27, NO. 5, MAY 2005


 lbp.zip (2个子文件)
lbp.zip (2个子文件)  27lbp.pdf 116KB
27lbp.pdf 116KB 37.pdf 1.04MB
37.pdf 1.04MB

 z14341344612022-03-14用户下载后在一定时间内未进行评价,系统默认好评。
z14341344612022-03-14用户下载后在一定时间内未进行评价,系统默认好评。 wtx1812872022-06-22用户下载后在一定时间内未进行评价,系统默认好评。
wtx1812872022-06-22用户下载后在一定时间内未进行评价,系统默认好评。 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功