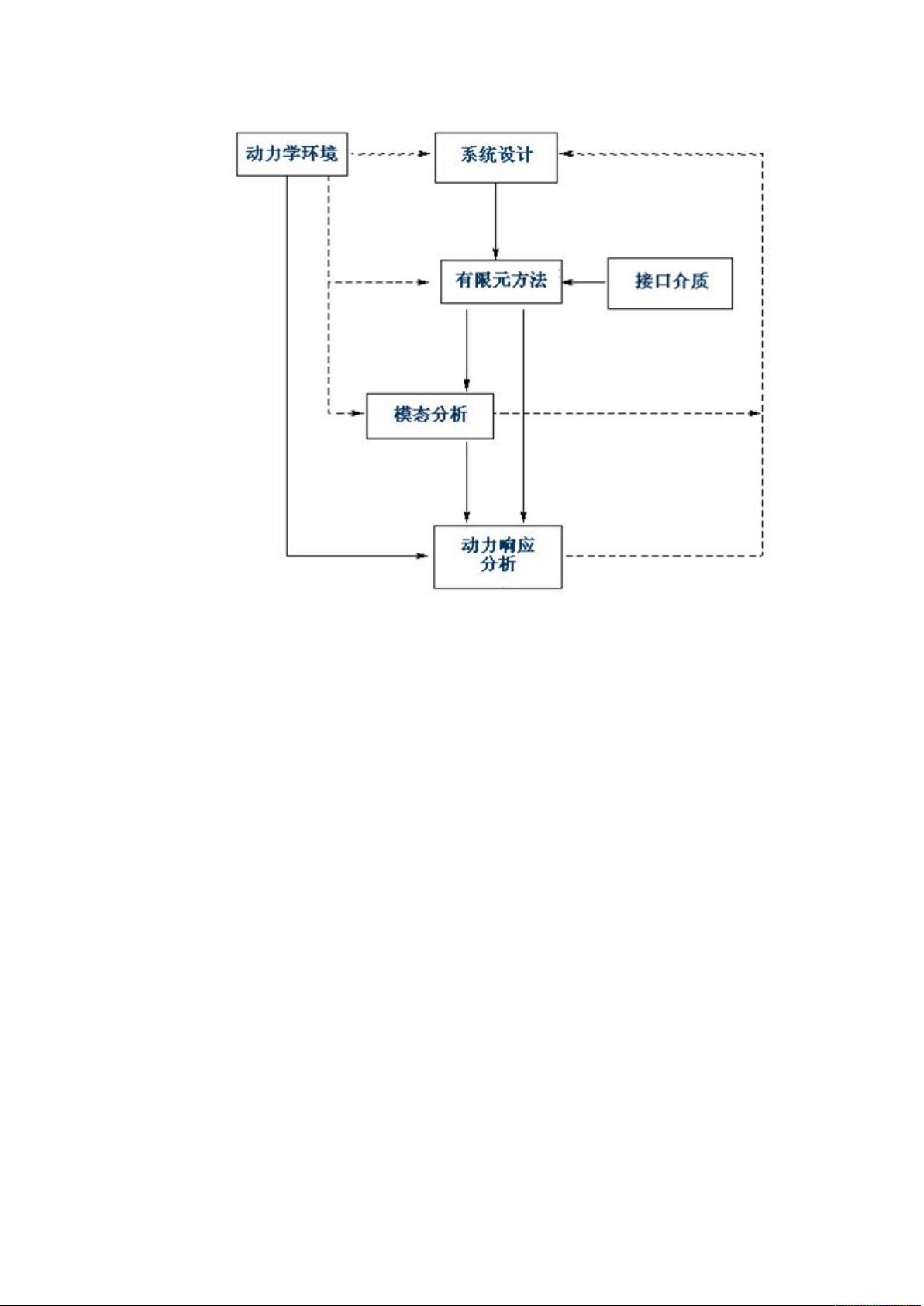
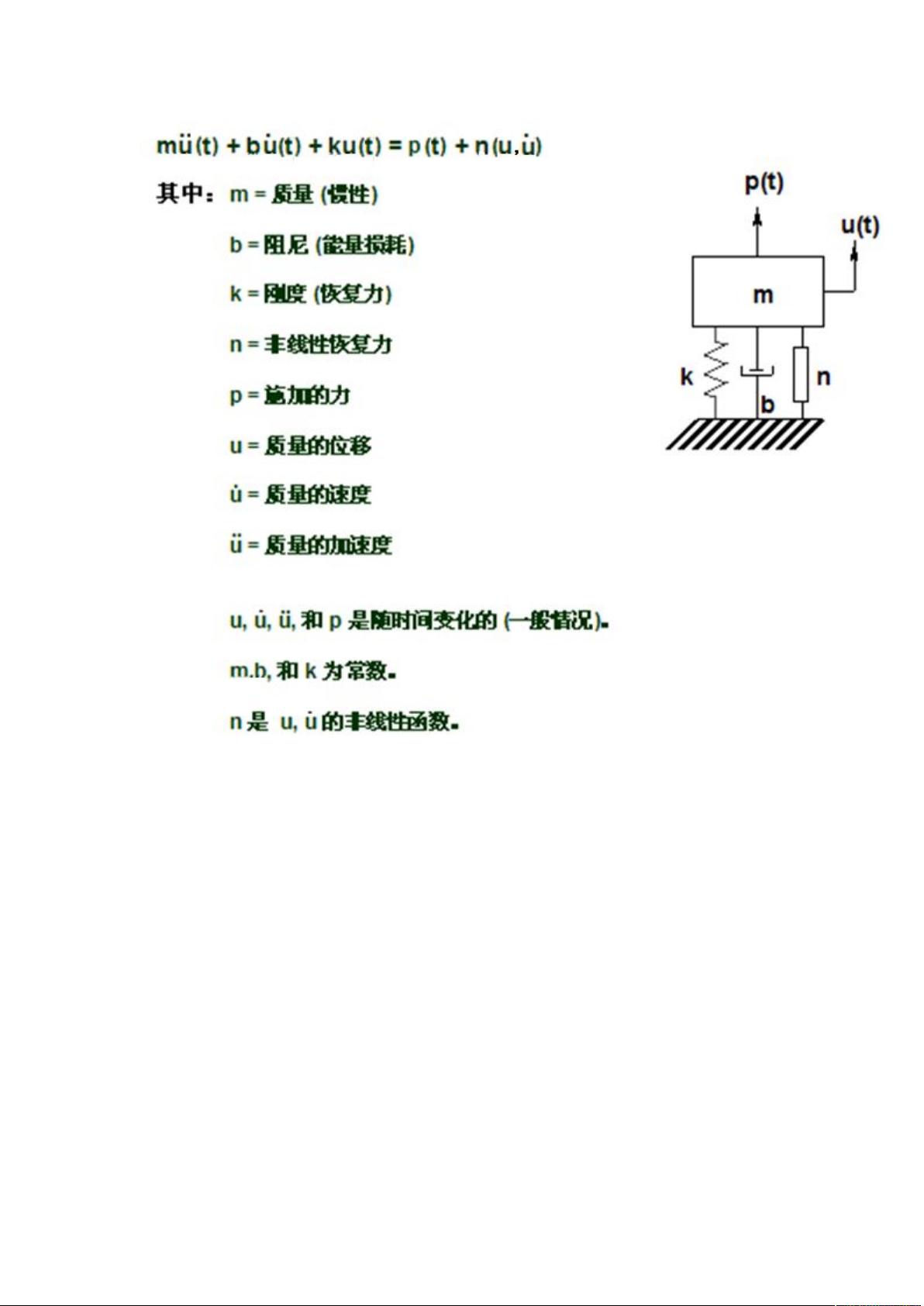
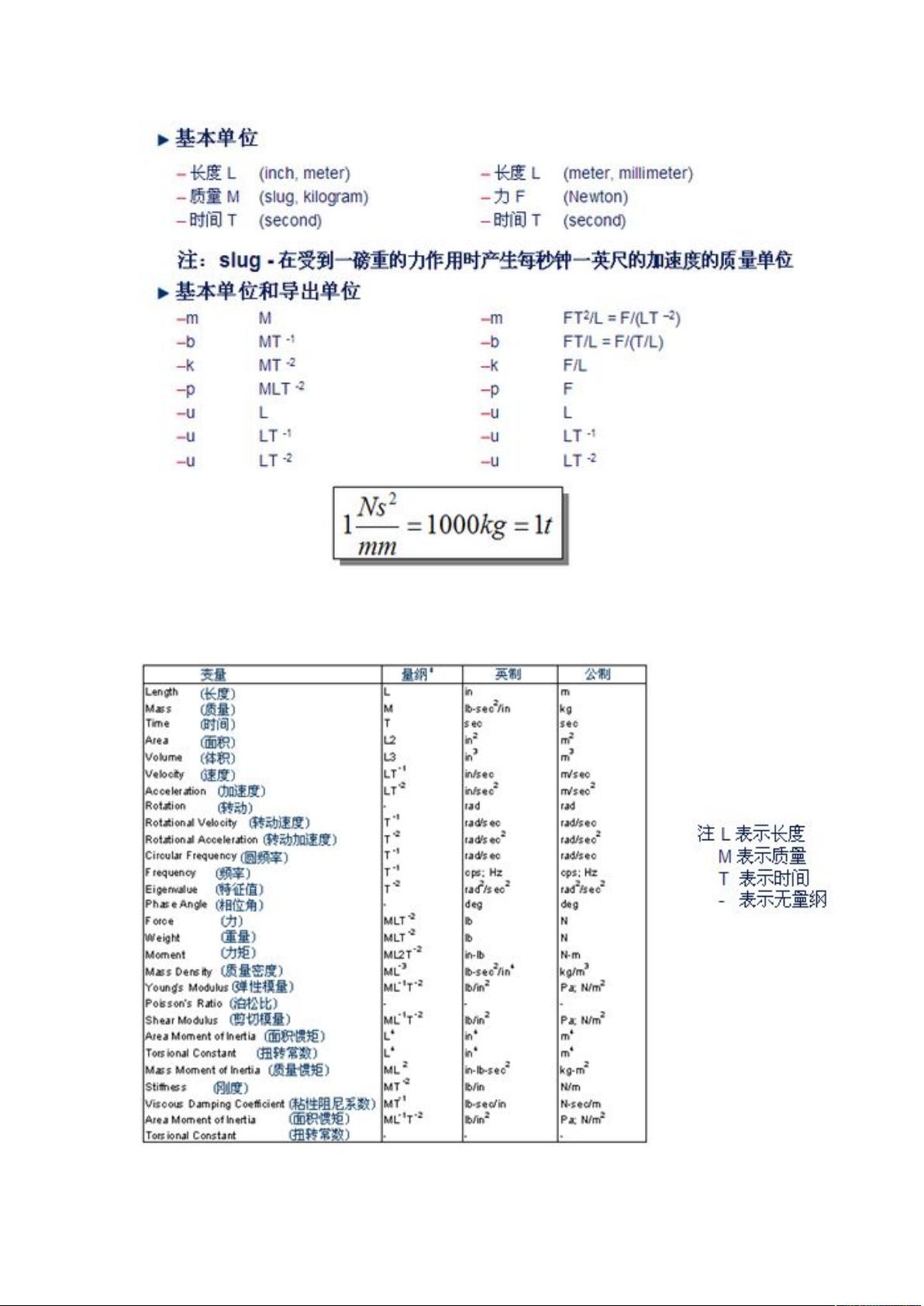
### NX Nastran动力学手册知识点总结
#### 一、理论基础回顾
1. **动力学分析过程**：动力学分析通常遵循一个标准化的过程，主要包括以下几个步骤：建立数学模型、求解模型、验证结果和解释结果。这个过程可以通过流程图的形式进行可视化表示。
2. **单自由度系统**
- **动力学运动方程**：单自由度系统的动力学运动方程为\[m\ddot{x} + c\dot{x} + kx = F(t)\]，其中\(m\)是质量，\(c\)是阻尼系数，\(k\)是刚度系数，\(F(t)\)是外力随时间的变化。
- **单位**：在进行动力学分析时，选择合适的单位非常重要。通常使用的单位包括牛顿(N)、秒(s)、米(m)等。需要注意的是，单位的一致性至关重要，错误的单位可能导致计算结果出现较大偏差。
- **无阻尼自由振动**：当系统没有阻尼时，振动方程简化为\[m\ddot{x} + kx = 0\]，其解为简谐振动\[x(t) = A\cos(\omega t + \phi)\]，其中\(A\)是振幅，\(\omega\)是角频率，\(\phi\)是初相位。
- **有阻尼自由振动**：有阻尼情况下的振动方程为\[m\ddot{x} + c\dot{x} + kx = 0\]。阻尼系数的不同会使得系统的振动特性发生变化，例如弱阻尼情况下，系统的振动将逐渐衰减。
- **单自由度系统的正弦振动**：对于无阻尼或有阻尼的单自由度系统，在正弦波激励下，系统的稳态解将呈现出特定的响应特性，这种响应通常可以通过放大因子来描述，放大因子与激励频率有关。
3. **多自由度系统**
- **概述**：多自由度系统的运动方程通常表示为\[\{M\}\{\ddot{u}\} + \{B\}\{\dot{u}\} + \{K\}\{u\} = \{P\}\]，其中\(\{u\}\)代表位移向量，\(\{M\}\)代表质量矩阵，\(\{B\}\)代表阻尼矩阵，\(\{K\}\)代表刚度矩阵，\(\{P\}\)代表外力向量。
- **动力学环境分类**：根据动力载荷的类型和来源，可以将动力学环境分为几类，例如静态载荷、动态载荷（如地震、风载荷）、瞬态载荷（如冲击）等。
- **有限元动力学建模的基本考虑**：在建立多自由度系统的动力学模型时，需要考虑的因素包括频率范围、节点/约束/单元的选择、线性或非线性的行为、是否采用超单元模型、与其他介质的相互作用、试验/测量数据的综合以及阻尼的处理方式等。
#### 二、常规模态分析
1. **定义**：常规模态分析是一种用于确定结构的动力特性的方法，主要包括固有频率和振型。
2. **应用**：通过常规模态分析，可以预测结构在不同激励下的响应特性，这对于结构的设计和优化具有重要意义。
#### 三、动力分析中的减缩
1. **概念**：动力分析中的减缩技术是指通过减少模型的自由度来简化计算，提高计算效率。
2. **方法**：常用的减缩方法包括子空间迭代法、刚体模态减缩法等。
#### 四、瞬态响应分析与频率响应分析
1. **瞬态响应分析**：瞬态响应分析关注的是系统在短时间内对外部激励的响应，通常适用于非周期性或瞬态载荷。
2. **频率响应分析**：频率响应分析则侧重于系统在稳态条件下的响应特性，主要用于评估系统对不同频率载荷的响应能力。
#### 五、其他相关知识点
1. **直接矩阵输入**：允许用户直接输入矩阵形式的数据，以便更灵活地控制计算过程。
2. **动力运动方程**：涉及动力学基本方程及其求解方法。
3. **残余矢量方法**：一种用于求解非线性问题的方法。
4. **强迫运动**：研究在外部强制运动下系统的响应特性。
5. **冲击和响应谱分析**：用于评估结构在冲击载荷作用下的响应。
6. **随机响应分析**：关注随机激励下系统的响应特性。
7. **复特征值分析**：用于解决包含阻尼的系统的动力学问题。
8. **使用局部超单元的常规模态分析**：利用局部超单元技术提高常规模态分析的效率。
9. **预加载结构的常规模态分析**：考虑预加载条件下的结构动力特性。
10. **动力设计优化**：结合动力学分析进行结构设计优化，提高结构性能。
11. **试验-分析相关性**：验证理论分析结果与实际测试数据的一致性，确保分析模型的准确性。
#### 六、参考文献
- W.C. Hurty and M.F. Rubinstein, Dynamics of Structures, Prentice-Hall, 1964.
- R.W. Clough and J. Penzien, Dynamics of Structures, McGraw-Hill, 1975.
- S. Timoshenko, D.H. Young, and W. Weaver Jr., Vibration Problems in Engineering, 4th Ed., John Wiley & Sons, 1974.
- K.J. Bathe and E.L. Wilson, Numerical Methods in Finite Element Analysis, Prentice-Hall, 1976.
- J.S. Przemieniecki, Theory of Matrix Structural Analysis, McGraw-Hill, 1968.
- C.M. Harris and C.E. Crede, Shock and Vibration Handbook, 2nd Ed., McGraw-Hill, 1976.
- L. Meirovitch, Analytical Methods in Vibrations, MacMillan, 1967.
- L. Meirovitch, Elements of Vibration Analysis, McGraw-Hill, 1975.
- M. Paz, Structural Dynamics: Theory and Computation, Prentice-Hall, 1981.
- W.T. Thomson, Theory of Vibrations with Applications, Prentice-Hall, 1981.
- R.R. Craig, Structural Dynamics: An Introduction to Computer Methods, John Wiley & Sons, 1981.
- S.H. Crandall and W.D. Mark, Random Vibration in Mechanical Systems, Academic Press, 1963.
- J.S. Bendat and A.G. Piersol, Random Data: Analysis and Measurement Procedures, John Wiley & Sons, 1986.
以上总结了NX Nastran动力学手册中的关键知识点，这些内容不仅涵盖了动力学理论的基础，还深入探讨了各种分析方法和技术，对于从事结构动力学分析的研究人员和工程师来说是非常宝贵的资源。
