
This is a Chapter from the Handbook of Applied Cryptography, by A. Menezes, P. van
Oorschot, and S. Vanstone, CR C Press, 1996.
For further information, see www.cacr.math.uwaterloo.ca/hac
CRC Press has granted the following specific permissions for the electronic vers ion of this
book:
Permission is granted to retrieve, print and store a single copy of this chapter for
personal use. This permission does not extend to binding multiple chapters of
the book, photocopying or producing copies for other than personal use of the
person creating the copy, or making electronic copies available for retrieval by
others without prior permissi on in writing from CRC Press.
Except where over-ridden by the specific permission abo ve, the standard copyright notice
from CRC Press applies to this electronic v ersion:
Neither this book nor any part may be reproduced or transmitted in any form or
by any means, electronic or mechanical, including photocopying, microfilming,
and recording, or by any information storage or retrieval system, without prior
permission in writing from the publisher.
The consent of CR C Press does not extend to copying for general distribution,
for promotion, for creating new works, or for resale. Specific permission must be
obtained in writing from CRC Press for such copying.
c
1997 by CRC Press, Inc.

Chapter
11
Digital Signatures
Contents in Brief
11.1 Introduction .............................425
11.2 A framework for digital signature mechanisms .......... 426
11.3 RSA and related signature schemes ................. 433
11.4 Fiat-Shamir signature schemes ................... 447
11.5 The DSA and related signature schemes .............. 451
11.6 One-time digital signatures ..................... 462
11.7 Other signature schemes ......................471
11.8 Signatures with additional functionality .............. 474
11.9 Notes and further references .................... 481
11.1 Introduction
This chapter considerstechniques designed to provide the digital counterpartto a handwrit-
ten signature. Adigital signatureof a messageisa number dependenton somesecret known
only to the signer, and, additionally, on the contentof the message being signed. Signatures
must be verifiable; if a dispute arises as to whether a party signed a document(caused by ei-
ther a lying signer trying to repudiate a signature it did create, or a fraudulent claimant), an
unbiased third party should be able to resolve the matter equitably, without requiringaccess
to the signer’s secret information (private key).
Digital signatures have many applications in information security, including authenti-
cation, data integrity, and non-repudiation. One of the most significant applications of dig-
ital signatures is the certification of public keys in large networks. Certification is a means
for a trusted third party (TTP) to bind the identity of a user to a public key, so that at some
later time, other entitiescan authenticatea public key without assistance froma trusted third
party.
The concept and utility of a digital signature was recognized several years before any
practical realizationwas available. The first method discovered was the RSA signaturesch-
eme, which remains today one of the most practical and versatile techniques available. Sub-
sequent research has resulted in many alternative digital signature techniques. Some offer
significant advantages in terms of functionality and implementation. This chapter is an ac-
count of many of the results obtained to date, with emphasis placed on those developments
which are practical.
425

426 Ch. 11 Digital Signatures
Chapter outline
§11.2 providesterminologyused throughoutthe chapter,anddescribesa frameworkfor dig-
ital signatures that permits a useful classification of the various schemes. It is more abstract
than succeeding sections. §11.3 provides an indepth discussion of the RSA signature sch-
eme, as well as closely related techniques. Standards which have been adopted to imple-
ment RSA and related signature schemes are also considered here. §11.4 looks at meth-
ods which arise from identification protocols described in Chapter 10. Techniques based
on the intractability of the discrete logarithm problem, such as the Digital Signature Algo-
rithm (DSA) and ElGamal schemes, are the topic of §11.5. One-time signature schemes,
many of which arise from symmetric-key cryptography, are considered in §11.6. §11.7 de-
scribes arbitrated digital signatures and the ESIGN signature scheme. Variations on the ba-
sic concept of digital signatures, including blind, undeniable, and fail-stop signatures, are
discussed in §11.8. Further notes, including subtle points on schemes documented in the
chapter and variants (e.g., designated confirmer signatures, convertible undeniable signa-
tures, group signatures, and electronic cash) may be found in §11.9.
11.2 A framework for digital signature mechanisms
§1.6 provides a brief introduction to the basic ideas behind digital signatures, and §1.8.3
shows how these signatures can be realized through reversible public-key encryption tech-
niques. This section describes two general models for digital signature schemes. A com-
plete understanding of the material in this section is not necessary in order to follow sub-
sequent sections; the reader unfamiliar with some of the more concrete methods such as
RSA (§11.3) and ElGamal (§11.5) is well advised not to spend an undue amount of time.
The idea of a redundancy function is necessary in order to understand the algorithms which
give digital signatures with message recovery. The notation provided in Table 11.1 will be
used throughout the chapter.
11.2.1 Basic definitions
1. A digital signature is a data string which associates a message (in digital form) with
some originating entity.
2. A digital signature generation algorithm (or signature generation algorithm)isa
method for producing a digital signature.
3. A digital signature verification algorithm (or verification algorithm) is a method for
verifying that a digital signature is authentic (i.e., was indeed created by the specified
entity).
4. A digital signature scheme (or mechanism) consists of a signature generation algo-
rithm and an associated verification algorithm.
5. A digital signature signing process (or procedure) consists of a (mathematical) digi-
tal signature generation algorithm, along with a method for formatting data into mes-
sages which can be signed.
6. A digital signature verification process (or procedure) consists of a verification algo-
rithm, along with a method for recovering data from the message.
1
1
Often little distinction is made between the terms scheme and process, and they are used interchangeably.
c
1997 by CRC Press, Inc. — See accompanying notice at front of chapter.

§
11.2 A framework for digital signature mechanisms 427
This chapter is, for the most part, concerned simply with digital signature schemes. In
order to use a digital signature scheme in practice, it is necessary to have a digital signature
process. Several processes related to various schemes have emerged as commercially rele-
vant standards; two such processes, namely ISO/IEC 9796 and PKCS #1, are described in
§11.3.5 and §11.3.6, respectively. Notation used in the remainder of this chapteris provided
in Table 11.1. The sets and functions listed in Table 11.1 are all publicly known.
Notation Meaning
M a set of elements called the message space.
M
S
a set of elements called the signing space.
S a set of elements called the signature space.
R a 1 − 1 mapping from M to M
S
called the redundancy function.
M
R
the image of R (i.e., M
R
=Im(R)).
R
−1
theinverseofR (i.e., R
−1
: M
R
−→ M).
R a set of elements called the indexing set for signing.
h a one-way function with domain M.
M
h
the image of h (i.e., h: M−→M
h
); M
h
⊆M
S
called the
hash value space.
Table 11.1:
Notation for digital signature mechanisms.
11.1 Note (comments on Table 11.1)
(i) (messages) M is the set of elements to which a signer can affix a digital signature.
(ii) (signing space) M
S
is the set of elements to which the signature transformations (to
be described in §11.2.2 and §11.2.3) are applied. The signature transformations are
not applied directly to the set M.
(iii) (signature space) S is the set of elements associated to messages in M. These ele-
ments are used to bind the signer to the message.
(iv) (indexing set) R is used to identify specific signing transformations.
A classification of digital signature schemes
§11.2.2 and §11.2.3 describe two general classes of digital signature schemes, which can be
briefly summarized as follows:
1. Digital signature schemes with appendix require the original message as input to the
verification algorithm. (See Definition 11.3.)
2. Digital signature schemes with message recovery do not require the original message
as input to the verification algorithm. In this case, the original message is recovered
from the signature itself. (See Definition 11.7.)
These classes can be further subdivided according to whether or not |R| =1, as noted in
Definition 11.2.
11.2 Definition A digital signature scheme (with either message recovery or appendix) is said
to be a randomized digital signature scheme if |R| > 1; otherwise, the digital signature
scheme is said to be deterministic.
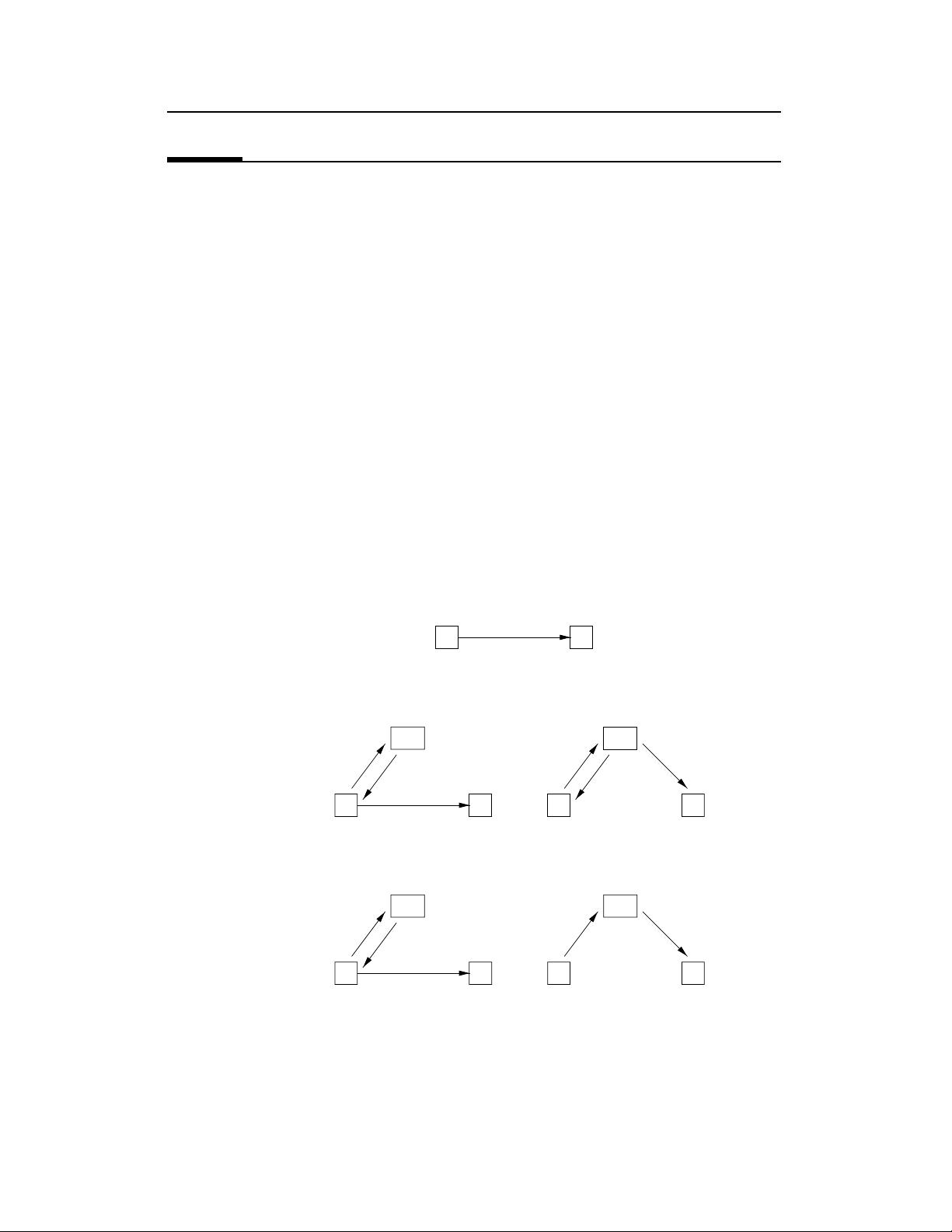
Figure 11.1 illustrates this classification. Deterministic digital signature mechanisms can
be further subdivided into one-time signature schemes (§11.6) and multiple-use schemes.
Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone.
428 Ch. 11 Digital Signatures
Digital signature schemes
message recovery
appendix
Randomized
Deterministic
Randomized
Deterministic
Figure 11.1:
A taxonomy of digital signature schemes.
11.2.2 Digital signature schemes with appendix
Digital signature schemes with appendix, as discussed in this section, are the most com-
monly used in practice. They rely on cryptographic hash functions rather than customized
redundancy functions, and are less prone to existential forgery attacks (§11.2.4).
11.3 Definition Digital signature schemes which require the message as input to the verifica-
tion algorithm are called digital signature schemes with appendix.
Examples of mechanisms providing digital signatures with appendix are the DSA
(§11.5.1), ElGamal (§11.5.2), and Schnorr (§11.5.3) signature schemes. Notation for the
following discussion is given in Table 11.1.
11.4 Algorithm Key generation for digital signature schemes with appendix
SUMMARY: each entity creates a private key for signing messages, and a corresponding
public key to be used by other entities for verifying signatures.
1. Each entity A should select a private key which defines a set S
A
= {S
A,k
: k ∈R}
of transformations. Each S
A,k
is a 1-1 mapping from M
h
to S and is called a signing
transformation.
2. S
A
defines a corresponding mapping V
A
from M
h
×Sto {true, false} such that
V
A
( em, s
∗
)=
true, if S
A,k
( em)=s
∗
,
false, otherwise,
for all em ∈M
h
, s
∗
∈S; here, em = h(m) for m ∈M. V
A
is called a verification
transformation and is constructed such that it may be computed without knowledge
of the signer’s private key.
3. A’s public key is V
A
; A’s private key is the set S
A
.
c
1997 by CRC Press, Inc. — See accompanying notice at front of chapter.
















评论0