自适应滤波器MATLAB仿真.doc

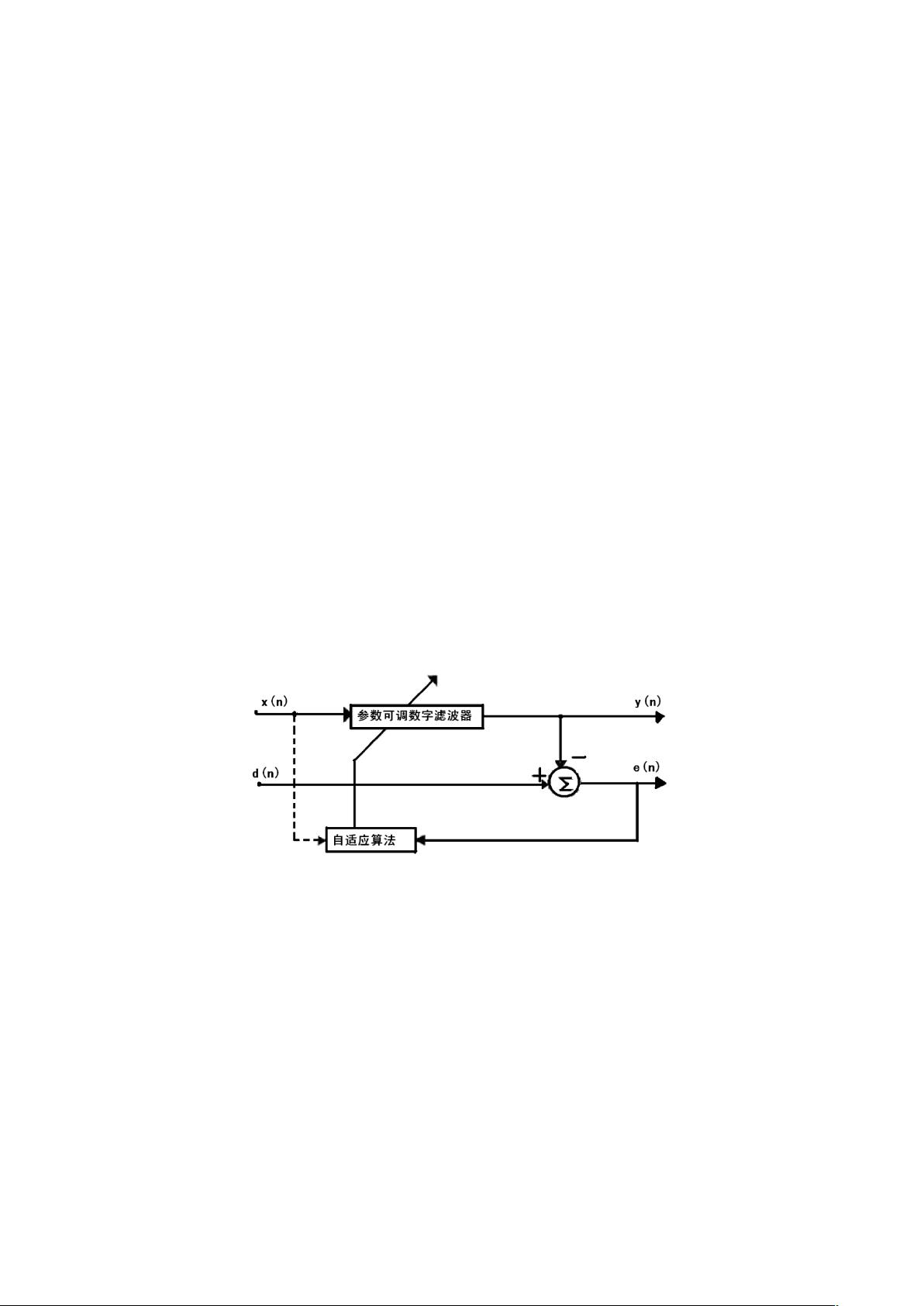
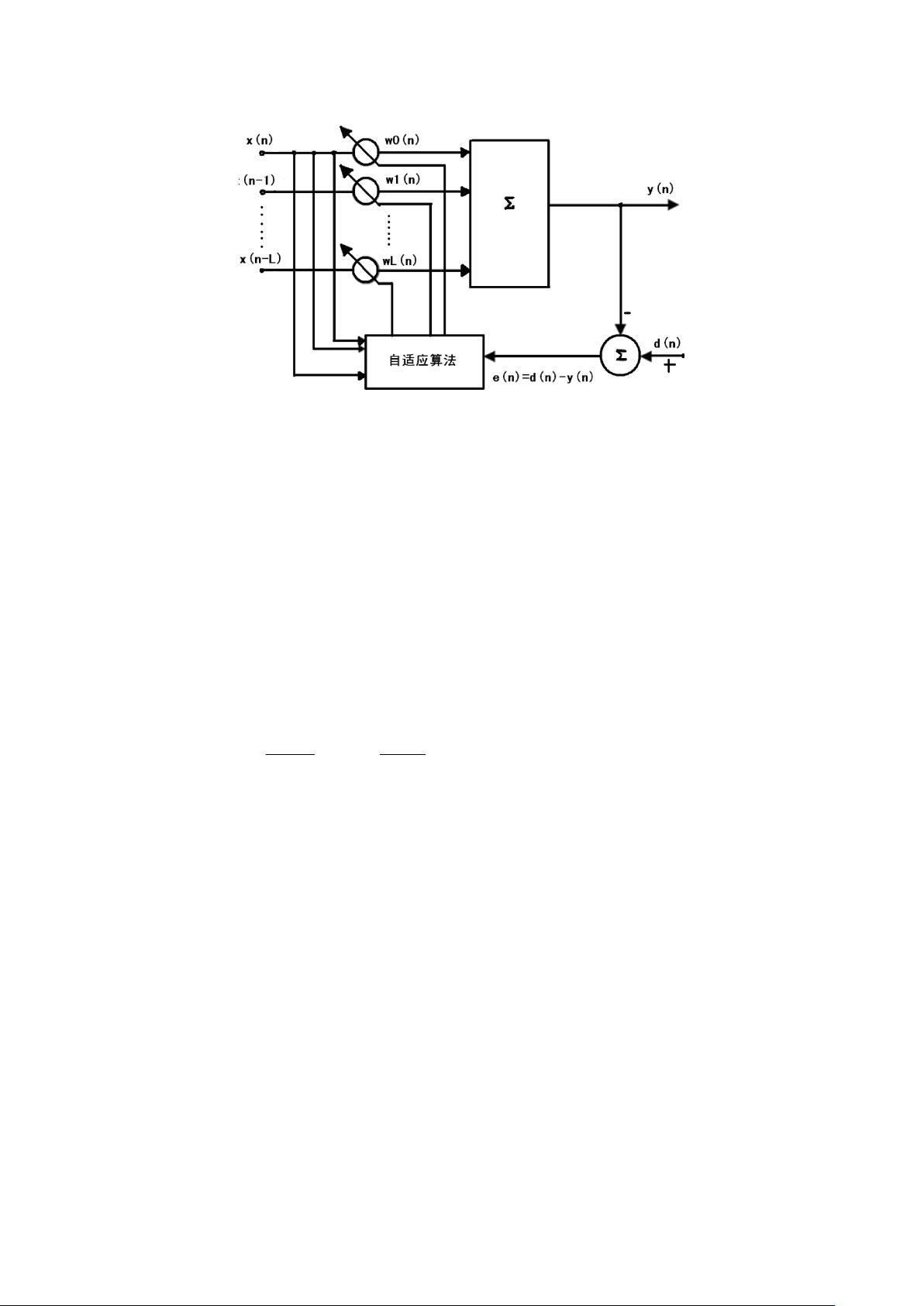
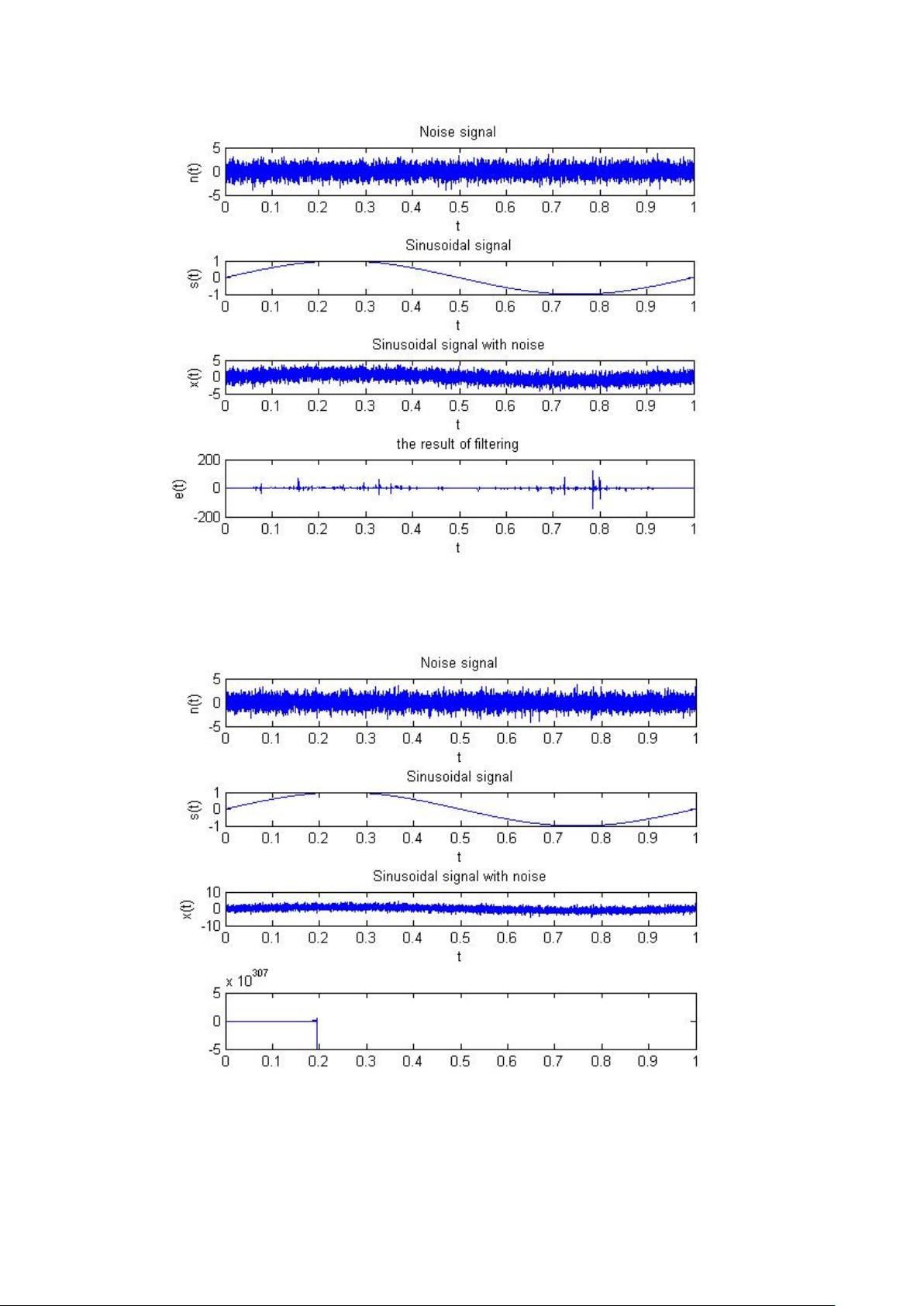
【自适应滤波器MATLAB仿真】文档主要探讨了自适应滤波器的工作原理和MATLAB7.0下的仿真过程，特别关注了最小均方误差（LMS）算法的应用。 自适应滤波器是一种最佳滤波方法，由Widrow B等人提出，它基于线性滤波理论，如维纳滤波和卡尔曼滤波。这种滤波器的优势在于其能自动适应信号环境，不需要预先了解信号和噪声的统计特性，就能实现最佳滤波效果。自适应滤波器通常由参数可调的FIR、IIR或格型滤波器组成，通过两个过程工作：输入信号通过滤波器得到输出，然后与参考信号比较产生误差信号；通过自适应算法调整滤波器参数，即权重系数，以达到最佳滤波状态。 LMS算法是自适应滤波中的核心算法，其思想是用平方误差作为优化目标，以简化计算。在实际应用中，滤波器参数的选择对滤波效果至关重要。例如，L阶加权自适应横向滤波器，其算法公式可以通过输入信号x(n)、权重系数w(n)和误差信号e(n)推导得出。误差信号e(n)是输出信号y(n)与参考信号d(n)之差，而误差信号的均方值E(e)则反映了滤波效果的好坏。通过计算梯度和最陡下降法迭代，可以更新权重系数w(n)，形成LMS算法的基本迭代公式。 在MATLAB7.0中，可以设计一个二阶FIR滤波器来模拟自适应滤波过程。生成一个标准正弦波信号s(n)和随机噪声信号n(n)，将两者相加得到带噪声的信号x(n)。然后，利用LMS算法的迭代公式（5），设计自适应滤波算法对噪声信号进行滤波，最终得到滤波后的信号e(n)。 自适应滤波器MATLAB仿真是研究和验证滤波器性能的有效工具，LMS算法是其关键组成部分。通过合理选择参数和实施仿真，可以观察滤波器对不同信号和噪声的处理能力，进一步优化滤波效果。对于学习和实践信号处理以及滤波理论的工程师和学生来说，这样的仿真具有很高的价值。