浦丰投针试验--MATLAB仿真.docx

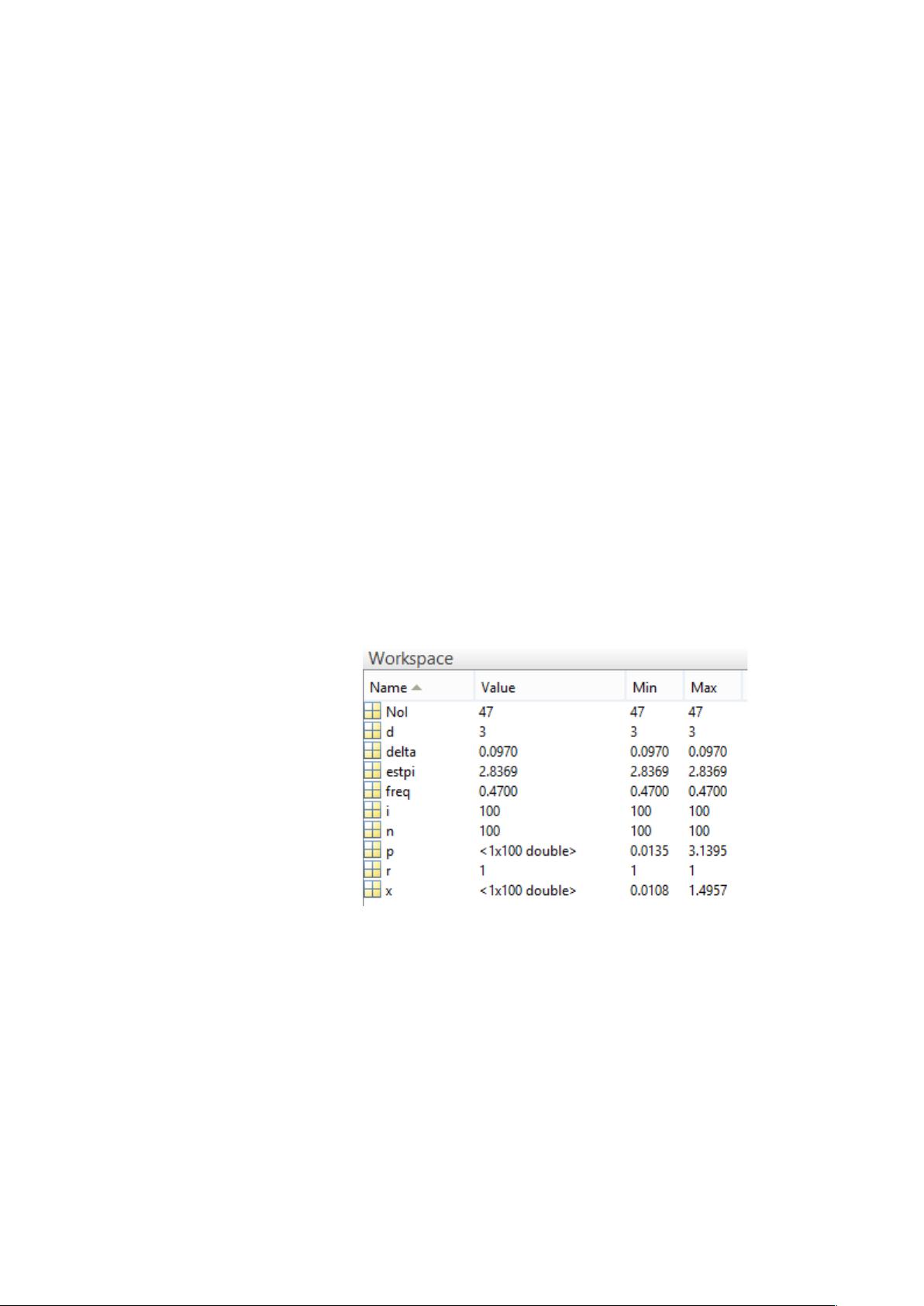
浦丰投针试验是一种经典的概率论实验，用于估算圆周率π。该实验基于几何概率原理，通过在纸上画平行线并随机投掷短针，记录针与线条相交的次数，进而推算π的值。MATLAB作为强大的数学计算软件，被用来模拟这一试验过程，从而提供了一种便捷的方法来估算π。 在MATLAB中，实验的基本步骤如下： 1. 设置参数：定义平行线间距d和针的长度l（l<d），以及针的长度的一半r。初始设定n为投针次数，例如100次。 2. 使用`rand`函数生成随机数：`x=d/2*rand(1,n)`生成针的随机起点位置，`p=pi*rand(1,n)`生成针与垂直方向的夹角。 3. 循环检查：通过`for`循环遍历所有投掷情况，使用条件判断`if x(i)<r*sin(p(i))`检查针是否与线条相交，如果相交，计数器NoI加1。 4. 计算频率(freq)：相交次数NoI除以总投掷次数n，得到针与线条相交的概率。 5. 估算π：利用公式`estpi=4*r/(d*freq)`计算圆周率的估计值。 6. 计算误差：通过`delta=abs(estpi-pi)/pi`计算相对于真实π值的相对误差。 实验过程中的观察发现，随着投掷次数n的增加，估算的π值的相对误差逐渐减小，表明样本量增大能够提高估计的准确性。同时，改变平行线间距d和针的长度l的比例d:r，也会影响估算的π值。当d/r增大时，估算的π值也呈现上升趋势。这表明平行线间距与针长比例对结果的影响，更宽的线条间距会导致π的估值偏高。 通过对不同n值和d:r比例的多次实验，可以总结出以下规律： 1. 投掷次数n增加，估算π的相对误差减小，估计值更加接近真实π值，体现了大数定律的作用。 2. d:r的比例增大，估算的π值也增大，这与几何概率的直观理解一致，因为更宽的线条间距使得针更容易相交，导致频率偏高，从而估算出较大的π值。 浦丰投针试验通过MATLAB仿真不仅能够提供一种直观有趣的π估算方法，还展示了概率统计在解决实际问题中的应用。通过调整实验参数，可以深入理解概率分布和样本大小对结果的影响，有助于提升对概率论和统计学的认识。