平行与垂直PPT.ppt

在几何学中，平面内的直线关系是基础概念之一，主要分为两类：相交和平行。这两类关系在我们的日常生活中有着广泛的应用，如建筑设计、道路规划等。本PPT主要探讨了平行线和垂直线的概念、性质以及如何识别它们。 让我们来看看平行线。在同一平面内，如果两条直线不相交，即无论延长多远，它们都不会相遇，那么这两条直线就被称作平行线。用专业术语来说，如果两条直线a和b满足这一条件，我们可以说直线a是直线b的平行线，反之亦然，或者直接说它们互相平行。这种关系可以用符号“∥”表示，如a∥b。平行线的一个关键特性是，它们之间的距离始终保持不变，这意味着任何通过一条平行线的平行线段都将与另一条平行线保持相同的距离。 接下来，我们转向垂直线。垂直线是在同一平面内相交的两条直线，但它们的特殊之处在于它们的夹角是90度，也就是直角。当两条直线形成直角时，我们说它们互相垂直。数学语言中，我们可以说直线a是直线b的垂线，反之亦然，或者a与b互相垂直，通常用符号"⊥"表示。垂足是两条垂直线相交的点，它标志着垂直关系的确立。 在实际操作中，我们可以使用小棒或其他直线物体来演示这些概念。例如，将三根小棒排列，使得其中一根与另外两根保持平行，然后检查剩下的两根小棒是否也互相平行。同样，若将两根小棒调整到与第三根垂直，我们可以发现它们也会形成90度的角，从而相互垂直。 需要注意的是，有时人们可能会混淆直线的关系。例如，认为两条直线的位置关系有平行、垂直、相交这三种，但实际上，相交线中只有一种特殊情况是垂直。另外，两条直线的交点称为交点，并非垂足，垂足特指垂直线的交点。不相交的两条直线确实被称为平行线，这个说法是正确的。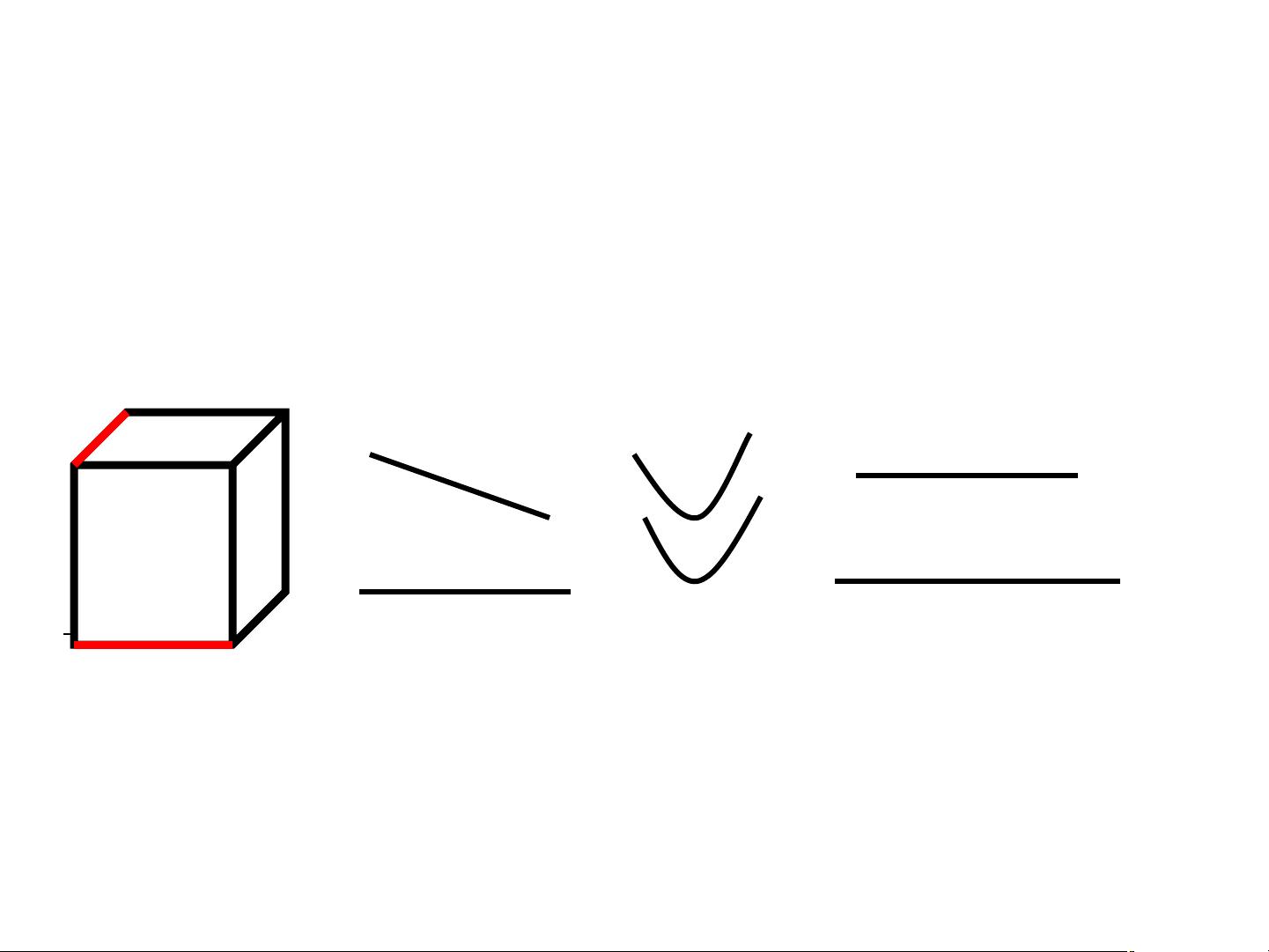 在给定的图例abcde中，可以找到多组平行线和垂直线。例如，直线a与直线b、直线c互相平行；直线d与直线e互相平行。至于垂直关系，有以下几组：直线a与直线d、直线b与直线d、直线c与直线d、直线a与直线e、直线b与直线e、直线c与直线e都是互相垂直的。这些关系可以通过观察它们之间的角度或使用直角工具来验证。 平行线和垂直线是平面几何的基本元素，理解它们的概念和性质对于解决几何问题至关重要。通过实例和练习，我们可以更好地掌握这些知识，并将其应用于实际问题中。