denoised gradually towards realistic samples [
25
,
64
,
66
].
The core building block in this process is a denoising au-
toencoder network that takes a noisy image and predicts the
denoising direction, equivalent to the score function [
30
,
71
].
This network, which is shared across different time steps of
the denoising process, is often a variant of U-Net [
25
,
57
]
that consists of convolutional residual blocks as well as self-
attention layers in several resolutions of the network. Al-
though the self-attention layers have shown to be impor-
tant for capturing long-range spatial dependencies, yet there
exists a lack of standard design patterns on how to incor-
porate them. In fact, most denoising networks often lever-
age self-attention layers only in their low-resolution feature
maps [
14
] to avoid their expensive computational complex-
ity. Recently, several works [
6
,
11
,
42
] have observed that
diffusion models exhibit a unique temporal dynamic dur-
ing generation. At the beginning of the denoising process,
when the image contains strong Gaussian noise, the high-
frequency content of the image is completely perturbed, and
the denoising network primarily focuses on predicting the
low-frequency content. However, towards the end of denois-
ing, in which most of the image structure is generated, the
network tends to focus on predicting high-frequency details.
The time dependency of the denoising network is often im-
plemented via simple temporal positional embeddings that
are fed to different residual blocks via arithmetic operations
such as spatial addition. In fact, the convolutional filters in
the denoising network are not time-dependent and the time
embedding only applies a channel-wise shift and scaling.
Hence, such a simple mechanism may not be able to opti-
mally capture the time dependency of the network during
the entire denoising process.
In this work, we aim to address the issue of lacking fine-
grained control over capturing the time-dependent compo-
nent in self-attention modules for denoising diffusion models.
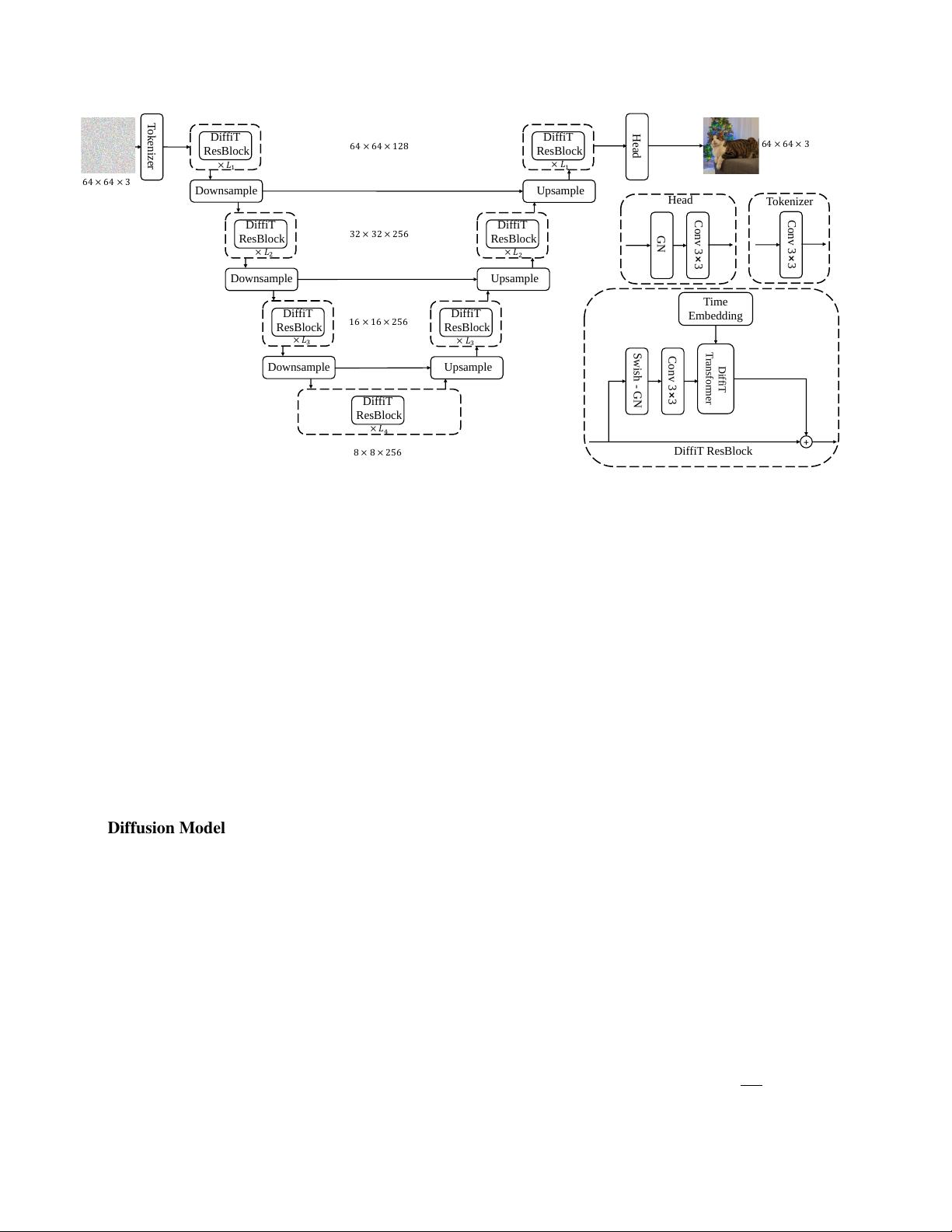
We introduce a novel Vision Transformer-based model for
image generation, called DiffiT (pronounced di-feet) which
achieves state-of-the-art performance in terms of FID score
of image generation on CIFAR10 [
43
] and FFHQ-64 [
32
]
(image space) as well as ImageNet-256 [
13
] and ImageNet-
512 [
13
] (latent space) datasets. Specifically, DiffiT proposes
a new paradigm in which temporal dependency is only in-
tegrated into the self-attention layers where the key, query,
and value weights are adapted per time step. This allows the
denoising model to dynamically change its attention mech-
anism for different denoising stages. In an effort to unify
the architecture design patterns, we also propose a hierarchi-
cal transformer-based architecture for latent space synthesis
tasks.
The following summarizes our contributions in this work:
•
We introduce a novel time-dependent self-attention mod-
ule that is specifically tailored to capture both short- and
long-range spatial dependencies. Our proposed time-
dependent self-attention dynamically adapts its behavior
over sampling time steps.
•
We propose a novel transformer-based architecture, de-
noted as DiffiT, which unifies the design patterns of de-
noising networks.
•
We show that DiffiT can achieve state-of-the-art perfor-
mance on a variety of datasets for both image and latent
space generation tasks.
2. Related Work
Transformers in Generative Modeling Transformer-
based models have achieved competitive performance in
different generative learning models in the visual domain [
10
,
15
,
16
,
27
,
79
,
80
]. A number of transformer-based archi-
tectures have emerged for GANs [
45
,
46
,
75
,
82
]. Trans-
GAN [
31
] proposed to use a pure transformer-based genera-
tor and discriminator architecture for pixel-wise image gen-
eration. Gansformer [
29
] introduced a bipartite transformer
that encourages the similarity between latent and image fea-
tures. Styleformer [
51
] uses Linformers [
72
] to scale the
synthesis to higher resolution images. Recently, a number
of efforts [
7
,
21
,
48
,
52
] have leveraged Transformer-based
architectures for diffusion models and achieved competitive
performance. In particular, Diffusion Transformer (DiT) [
52
]
proposed a latent diffusion model in which the regular U-Net
backbone is replaced with a Transformer. In DiT, the condi-
tioning on input noise is done by using Adaptive LayerNorm
(AdaLN) [
53
] blocks. Using the DiT architecture, Masked
Diffusion Transformer (MDT) [
21
] introduced a masked
latent modeling approach to effectively capture contextual
information. In comparison to DiT, although MDT achieves
faster learning speed and better FID scores on ImageNet-256
dataset [
13
], it has a more complex training pipeline. Unlike
DiT and MDT, the proposed DiffiT does not use shift and
scale, as in AdaLN formulation, for conditioning. Instread,
DiffiT proposes a time-dependent self-attention (i.e. TMSA)
to jointly learn the spatial and temporal dependencies. In ad-
dition, DiffiT proposes both image and latent space models
for different image generation tasks with different resolu-
tions with SOTA performance.
Diffusion Image Generation Diffusion models [
25
,
64
,
66
] have driven significant advances in various domains,
such as text-to-image generation [
6
,
54
,
59
], natural language
processing [
47
], text-to-speech synthesis [
41
], 3D point
cloud generation [
77
,
78
,
84
], time series modeling [
67
],
molecular conformal generation [
74
], and machine learning
security [
50
]. These models synthesize samples via an itera-
tive denoising process and thus are also known in the com-
munity as noise-conditioned score networks. Since its initial
success on small-scale datasets like CIFAR-10 [
25
], diffu-
sion models have been gaining popularity compared to other
2
