没有合适的资源?快使用搜索试试~ 我知道了~
温馨提示
Unsupervised Learning: Neighbor Embedding Manifold Learning Locally Linear Embedding (LLE) Laplacian Eigenmaps T-distributed Stochastic Neighbor Embedding (t-SNE)
资源推荐
资源详情
资源评论

Unsupervised Learning:
Neighbor Embedding
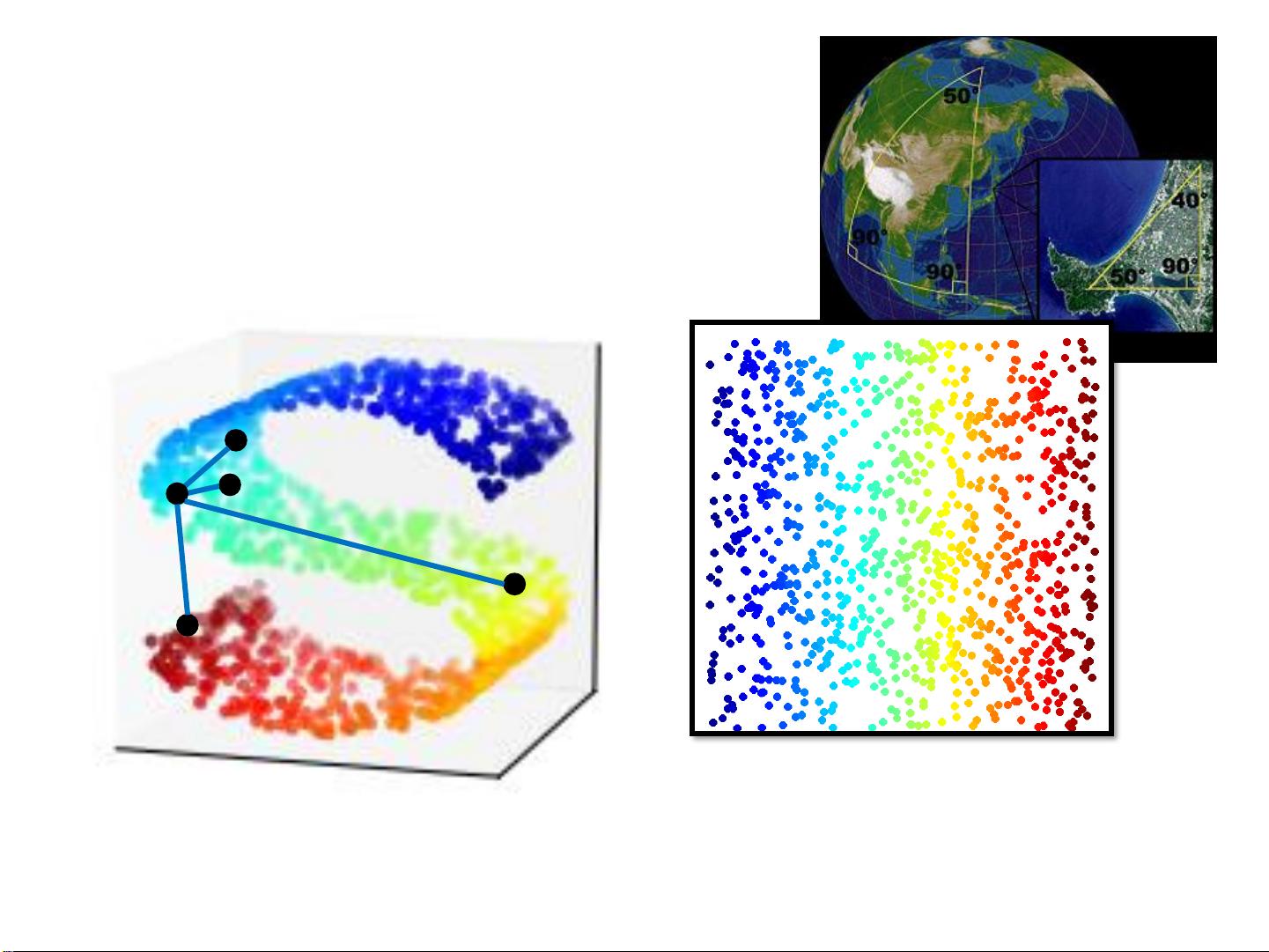
Manifold Learning
Suitable for clustering or
following supervised learning
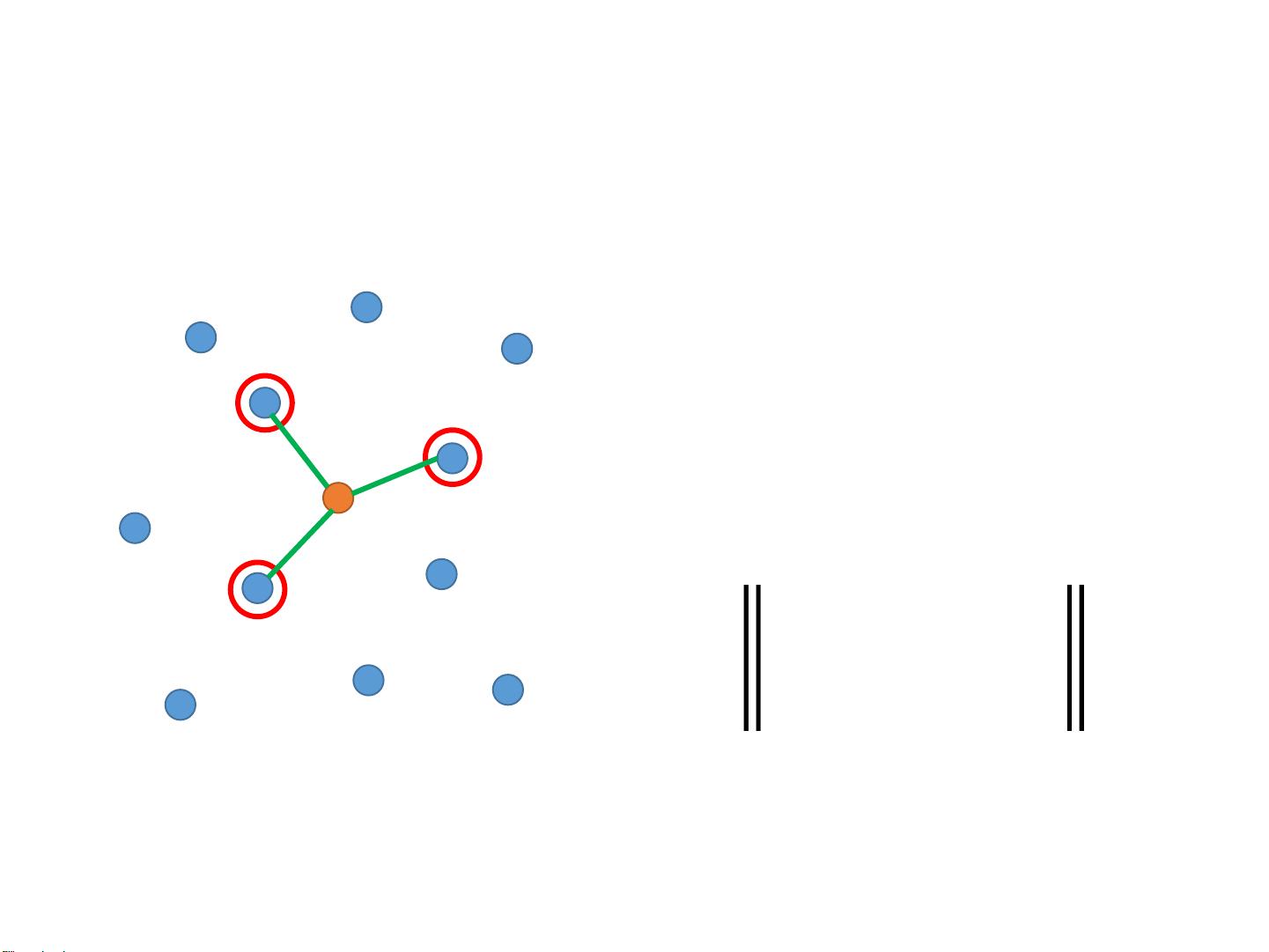
Locally Linear Embedding (LLE)
𝑥
𝑖
𝑥
𝑗
𝑤
𝑖𝑗
𝑤
𝑖𝑗
represents the relation
between 𝑥
𝑖
and 𝑥
𝑗
Find a set of 𝑤
𝑖𝑗
minimizing
𝑖
𝑥
𝑖
−
𝑗
𝑤
𝑖𝑗
𝑥
𝑗
2
Then find the dimension reduction results
𝑧
𝑖
and 𝑧
𝑗
based on 𝑤
𝑖𝑗
剩余14页未读,继续阅读
资源评论

fdtsaid
- 粉丝: 186
- 资源: 86
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 现场评定检查表——建筑外墙、屋面保温和建筑外墙装饰.docx
- 现场评定检查表--气体灭火系统.docx
- 消防第三方技术服务模拟验收抽查记录表.doc
- 现场评定检查表——总平面布局.docx
- 消防验收过程服务--现场记录表.doc
- 消防第三方技术服务现场交底监督记录表.doc
- 向日葵被控端绿色精简运行版
- 学生心理档案表.docx
- 验收确认单表格.docx
- 阳宅净宅表文.docx
- 医疗废弃物建设项目环境风险简单分析表.docx
- 原材料检测报告.docx
- 造林补助实施方案小班一览表、造林补助(新增部分)分行政村(国有林场)任务落实情况表.xls
- 造林补助(新增部分)分行政村(国有林场)任务落实情况表.docx
- 肢体残疾标准.docx
- 职工工伤与职业病致残等级分级表十级.docx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功