1
第三章 匹配理论
§3.1 匹配与最大匹配
定义3.1.1 设G 是一个图, )(GEM ⊆ ,满足:对
i
e
∀
, Me
j
∈
,
i
e 与
j
e 在 G 中不相邻,则称
M
是 G 的一个匹配。对匹配
M
中每条边 uve
=
,其两端点u和v称为被匹配
M
所匹配,而u和v
都称为是
M
饱和的(saturated vertex)。
注:每个顶点要么未被
M
饱和,要么仅被
M
中一条边饱和。
定义3.1.2 设
M
是 G 的一个匹配,若 G 中无匹配
M
′
,使得 |||| MM >
′
,则称
M
是 G 的一个
最大匹配;如果
G 中每个点都是
M
饱和的,则称
M
是 G 的完美匹配(Perfect matching).
显然,完美匹配必是最大匹配。
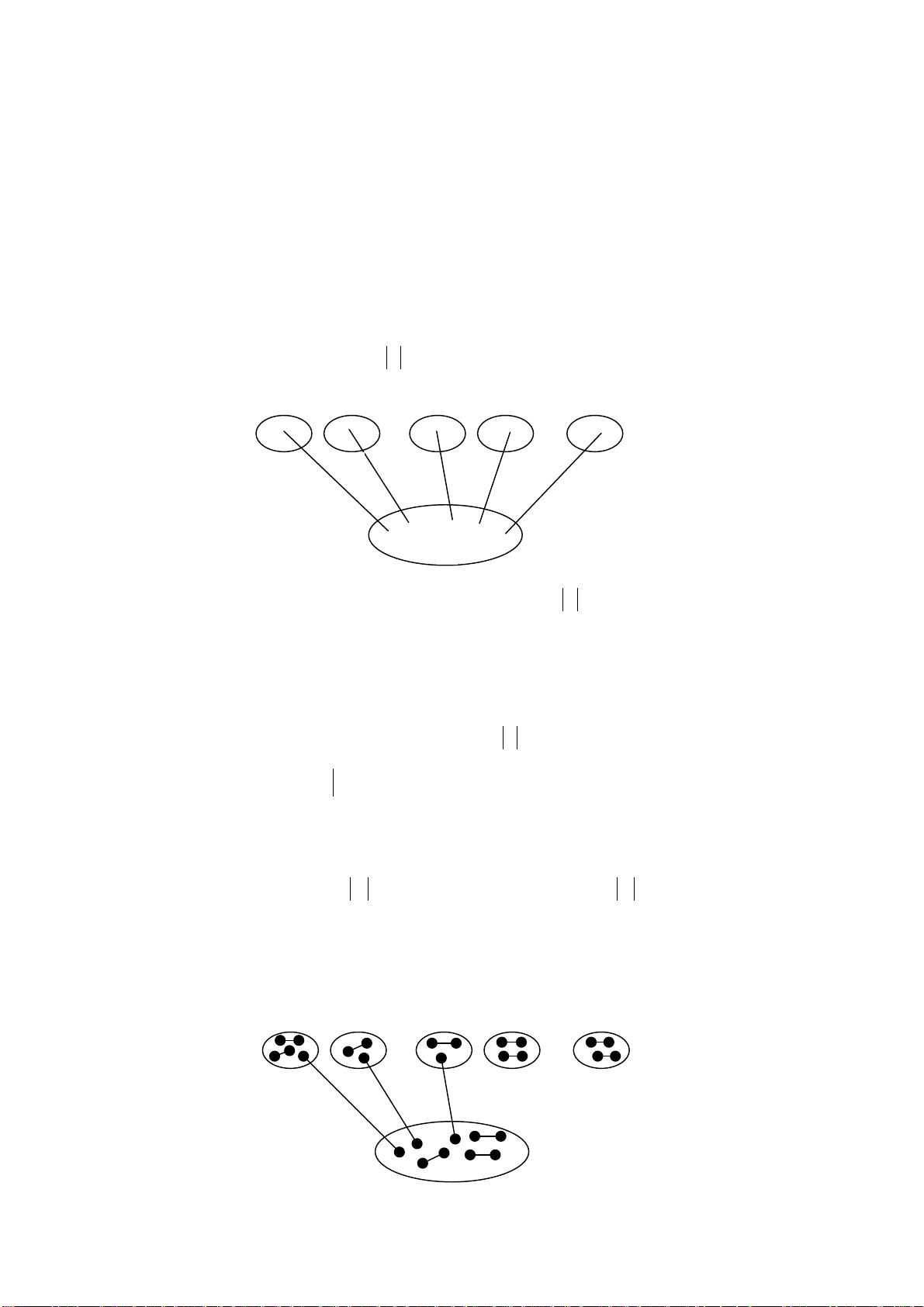
定义3.1.3 设
M
是 G 的一个匹配, G 的
M
交错路是指其边
M
和 MGE \)( 中交替出现的
路。如果 G 的一条
M
交错路(alternating path)的起点和终点都是
M
非饱和的,则称其为一条
M
可扩展路或
M
增广路(augmenting path)。
定理 3.1.1(Berge,1957) 图
G 的匹配
M
是最大匹配的充要条件是G中不存在
M
可扩展路。
证明:必要性:设
M
是 G 的一个最大匹配。如果 G 中存在一个
M
可扩展路 P,则将 P 上所有不
属于
M
的边构成集合
M
′
。显 然
M
′
也是 G 的一个匹配且比
M
多一条边。这与
M
是最大匹配
相矛盾。
充分性:设
G 中不存在
M
可扩展路。若匹配
M
不是最大匹配,则存在另一匹配
M
′
,使
|||| MM >
′
.
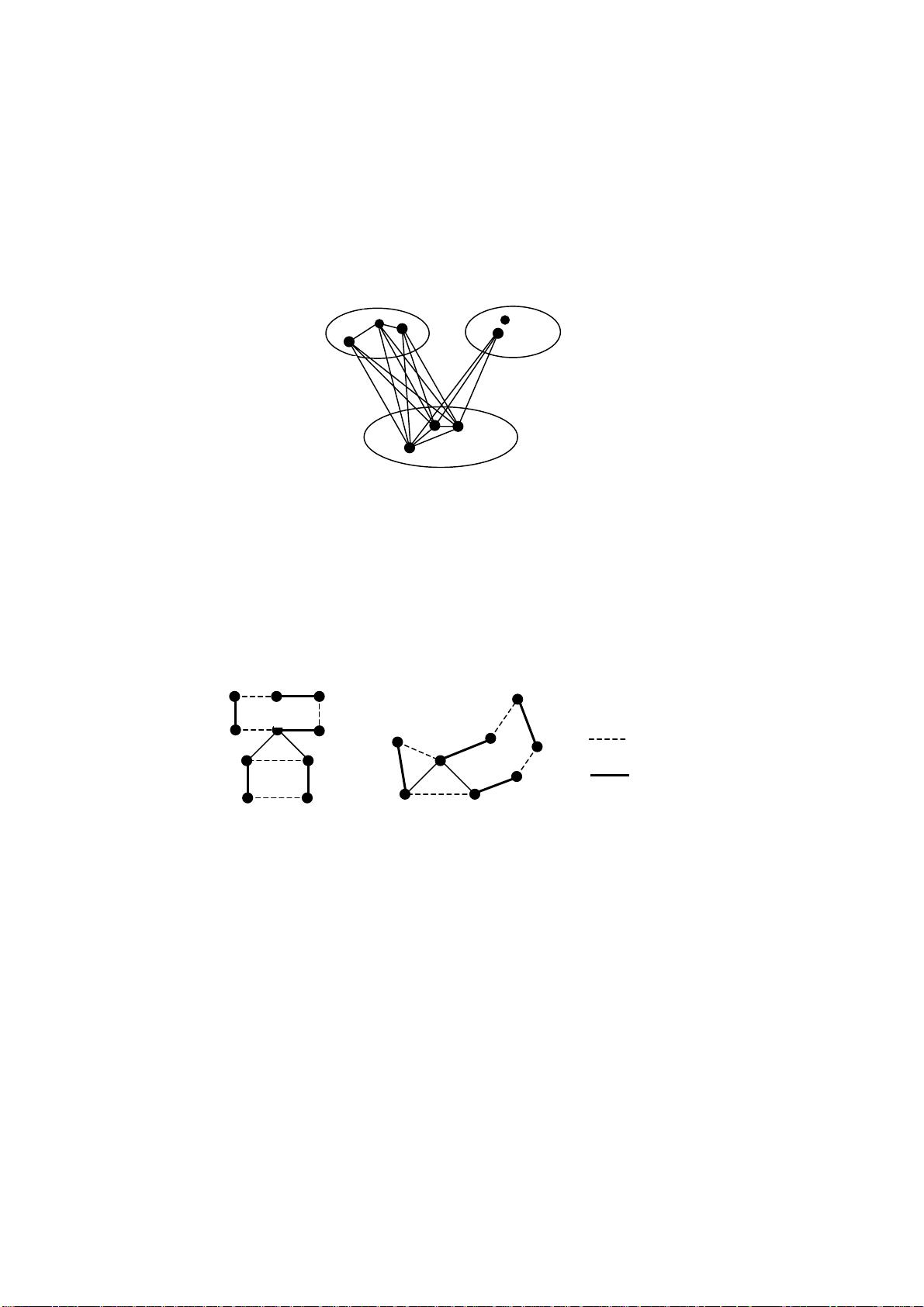
令
][ MMGH
′
⊕= ,( MMMMMM
′
−
′
=
′
⊕
IU 称为对称差)。
则
H
中每个顶点的度非1即2(这是因为一个顶点最多只与
M
的一条边及
M
′
的一条边相关
联)。故
H
的每个连通分支要么是
M
的边与
M
′
的边交替出现的一个偶长度圈,要么是
M
的
边与
M
′
的边交替出现的一条路。由于 |||| MM >
′
,
H
的边中
M
′
的边多于
M
的边,故必有
H
的某个连通分支是一条路,且始于
M
′
的边又终止于
M
′
的边。这条路是一条
M
可扩展路。这
与条件矛盾。 证毕。