三角形的内切圆和外接圆.pdf

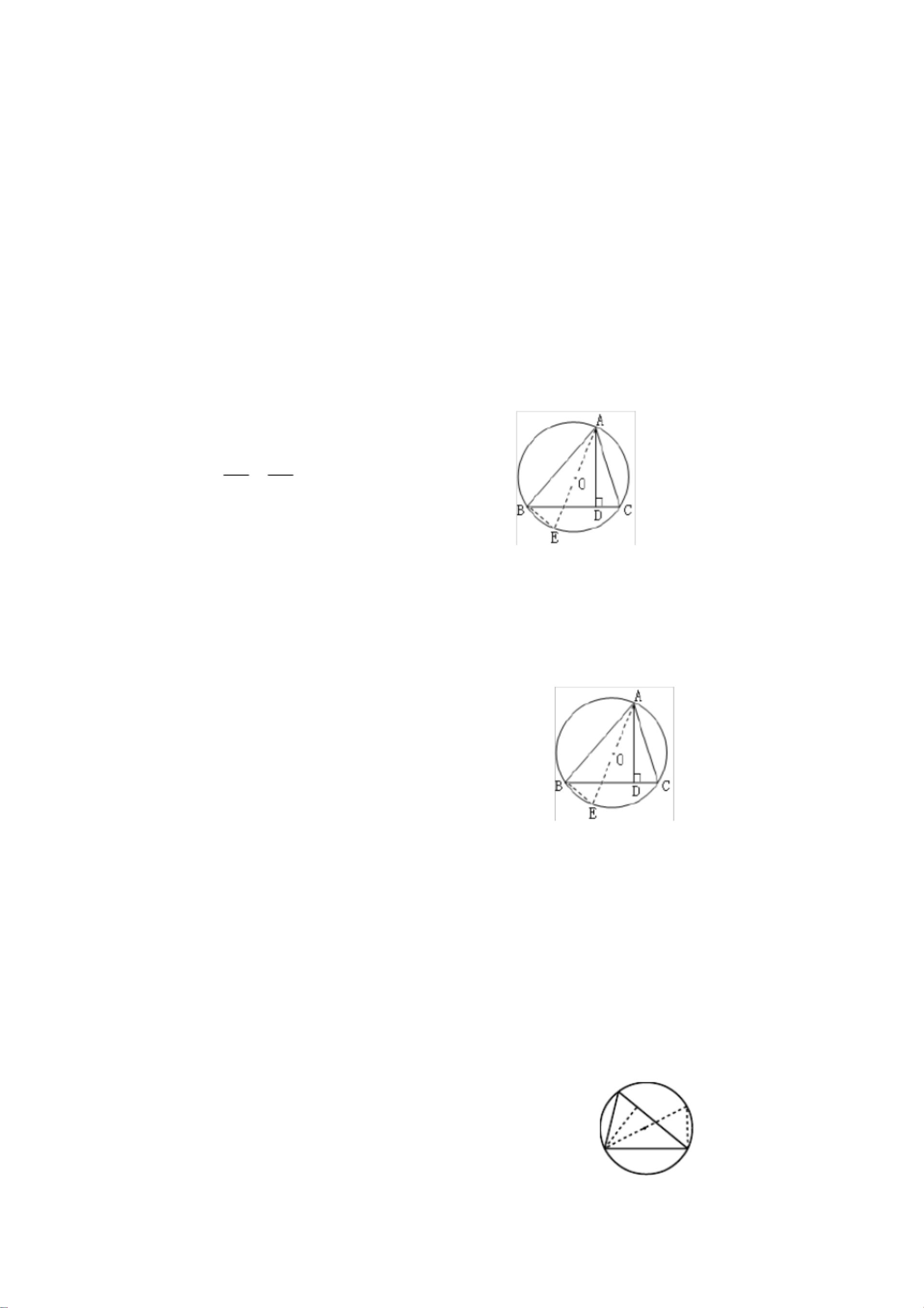
三角形的外接圆是指一个圆能够通过三角形的三个顶点，这样的圆称为外接圆，而外接圆的中心被称为三角形的外心。外心是三角形三条边的垂直平分线的交点，它具有特性，即外心到三角形每个顶点的距离相等。对于锐角三角形，外心位于三角形内部，而对于钝角三角形，外心位于三角形外部。在直角三角形中，外心恰好是斜边的中点，且外接圆的半径\( R \)与斜边长度\( c \)之间的关系为\( R = \frac{c}{2} \)。 外接圆半径的求法有多种，其中一种是利用公式\( R = \frac{ab}{2h} \)，这里的\( a \)和\( b \)是三角形两边的长度，\( h \)是这两边所夹角的对边上的高。另外，如果知道三角形的某个内角\( A \)和其对边\( a \)，可以利用正弦定理得到\( 2R = \frac{a}{\sin A} \)来求外接圆半径。 三角形内切圆则是与三角形三边都相切的圆，内切圆的圆心称为内心，是三角形三条内角平分线的交点。内心到三角形每条边的距离相等，并且内心总是位于三角形的内部。内切圆半径\( r \)可以通过三角形的面积\( S \)和周长\( p \)来计算，公式为\( r = \frac{2S}{p} \)。对于直角三角形，如果\( a \)和\( b \)是直角边，\( c \)是斜边，那么内切圆半径的另一种表达方式为\( r = \frac{ab}{a+b+c} \)或者\( r = \frac{c}{2}( \frac{1}{a} + \frac{1}{b} - \frac{1}{c}) \)。 圆内接四边形的性质指出，内接四边形的对角互补，也就是说，四边形的每个内角加上其相对的外角等于180度。此外，圆内接梯形是等腰梯形，而圆内接平行四边形是矩形。 在解决实际问题时，我们可以利用这些知识来求解外接圆半径。例如，已知三角形的三边长，可以使用\( R = \frac{ab}{2h} \)来求外接圆半径，而如果已知两边长和夹角，可以利用正弦定理\( 2R = \frac{a}{\sin A} \)来计算。同时，通过三角形的面积和周长也可以求得内切圆半径。 理解和掌握三角形的外接圆和内切圆的性质及其半径的计算方法，对于解决几何问题至关重要，尤其是在处理涉及圆的几何图形时。通过上述的知识点，我们能够有效地解决一系列与三角形及其圆相关的问题。