问题一:
利用均匀分布 UL-1,1],使用中心极限定理产生生正态分布的随机数 1000 个,
其中每次用于产生正态分布随机数的均匀分布样木容量 n>50
一.问题描述
中心极限定理给出随机变量平均值的分布情况,假如随机变量 X_{1} ...X_{n} 相互
独立, 服从同一分布,当 n 充分大时,则其随机变量之和的分布函数服从正态分
布。本题首先利用均匀分布选取 50 个以上的样本,然后对所取样本取和获得一
个随机数。独立重复上述过程 1000 次,获得 1000 个随机数,检验其是否符合正
态随机分布。
二.理论分析与理论结果
理论分析:中心极限定理的应用有着所使用的随机变量之间相互独立的前提,因
此需选取[-1,1]之间相互独立的随机数。本题中,应通过均匀分布 U[-1,1]随机选
取 100 个随机变量并求和作为随机数,选取的 1000 组随机数间应不存在任何关
联,相互独立。根据大数定理:n 个相互独立的随机变量,在 n 充分大时满足随
机变量之和的分布服从正态分布。即本实验中的 1000 组随机数的分布符合正态
分布。
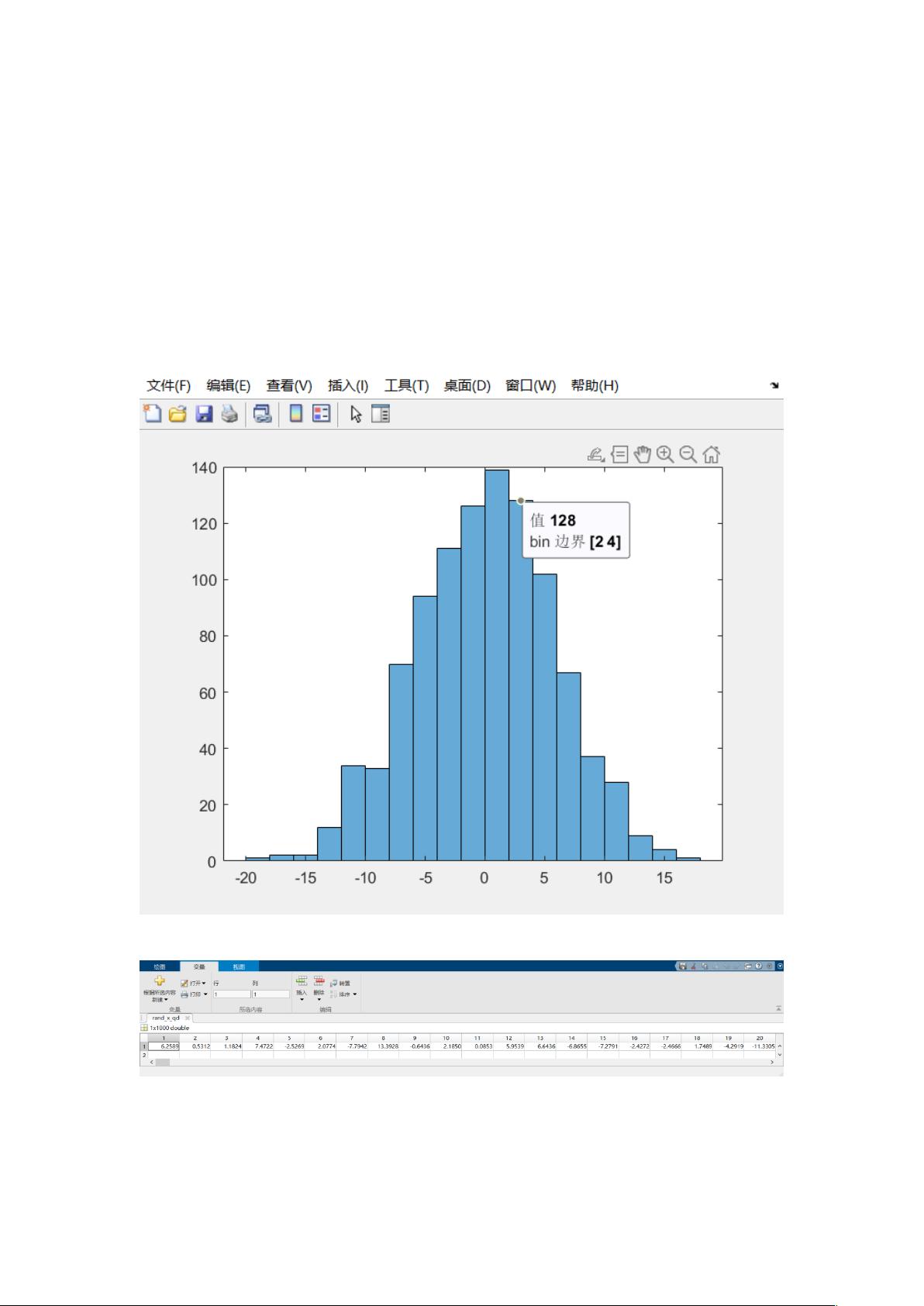
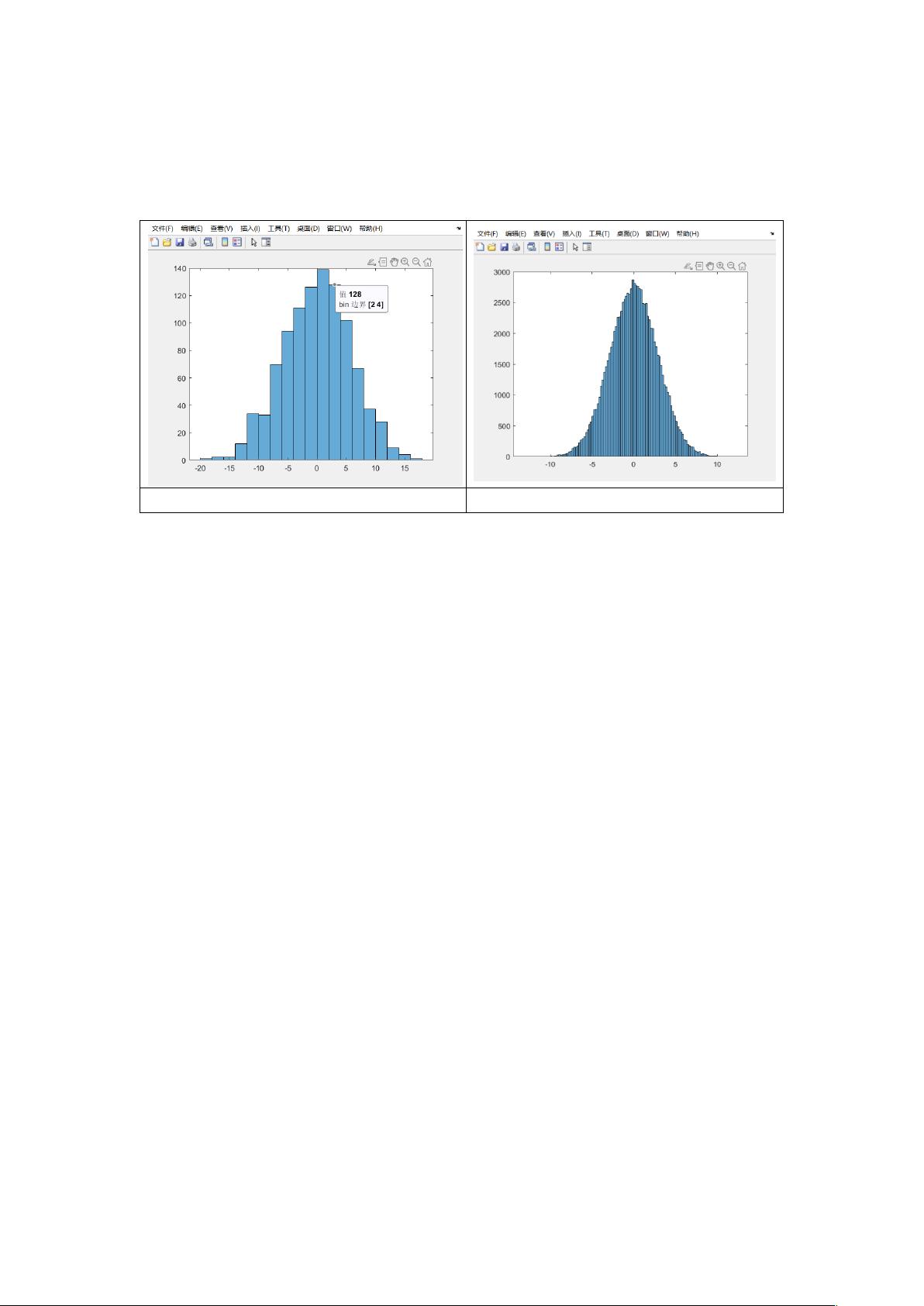
理论结果:随机变量之和即随机数的均值接近 0,总体分布接近为正态分布。
三.MATLAB 程序介绍和程序源代码
rand_x_qd = [];
for t = 1:1000
rand_x_qd = [rand_x_qd,my_rand()];
end
##循环 1000 次产生随机变量的函数产生 1000 个随机数
histogram(rand_x)
##画出随机数的分布图
function result = my_rand()