传染病模型SI、SIS、SIR
传染病模型是数学流行病学的基础,它们描述了传染病在人群中的传播过程。其中,SI 模型、SIS 模型和 SIR 模型是最基本和最重要的三种传染病模型。
SI 模型是最简单的传染病模型,它假设感染个体可以传染其他个体,并且一旦感染就不能康复。该模型的数学表达式为:
dy/dt = a * (y - y^2)
其中,y 是感染个体的数量,a 是传染率。
使用 MATLAB 可以求解 SI 模型的解析解:
y = 1 / (1 - exp(-a*t) * (1 - y0) / y0)
其中,y0 是初始感染个体的数量。
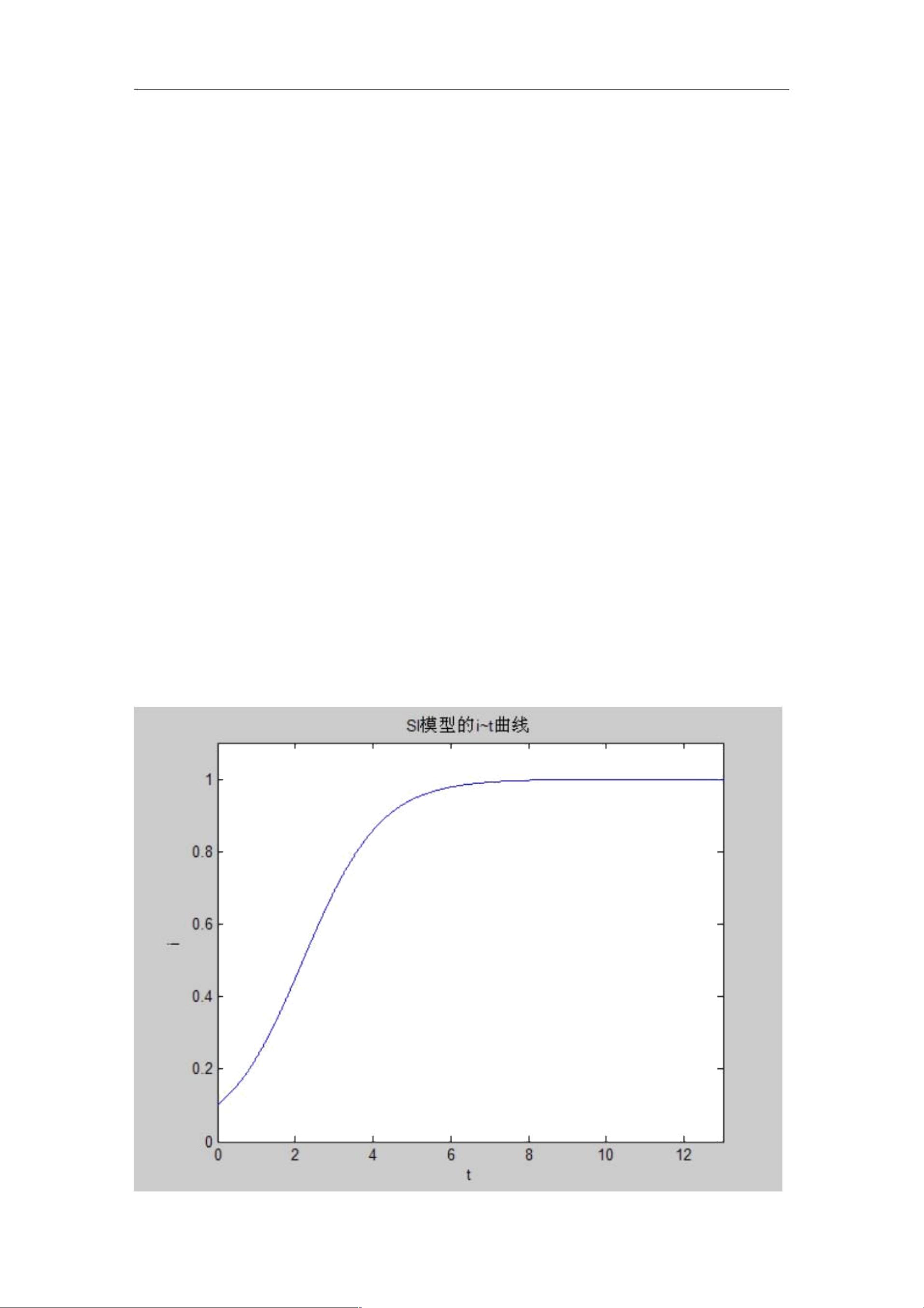
画图:SI 模型的 i~t 曲线
在 MATLAB 中,可以使用以下命令画出 SI 模型的 i~t 曲线:
>> y = 1 ./ (1 + 9 * exp(-t));
>> plot(t, y);
>> title('SI 模型的 i~t 曲线 ');
>> xlabel('t');
>> ylabel('i');
画图:SI 模型的 di/dt~i 曲线
在 MATLAB 中,可以使用以下命令画出 SI 模型的 di/dt~i 曲线:
>> x = 0:0.01:1;
>> y = x - x.^2;
>> plot(x, y);
>> title('SI 模型的 di/dt~i 曲线 ');
>> xlabel('i');
>> ylabel('di/dt');
SIS 模型是 SI 模型的扩展,它假设感染个体可以康复,并且康复后的个体不能再次感染。该模型的数学表达式为:
dy/dt = a * (y - y^2) - b * y
其中,y 是感染个体的数量,a 是传染率,b 是康复率。
使用 MATLAB 可以求解 SIS 模型的解析解:
y = (a - b) / (a - exp(-(a - b) * t) * (a - b + y0 * a) / y0 / (a - b) * a + exp(-(a - b) * t) * (a - b + y0 * a) / y0 / (a - b) * b)
其中,y0 是初始感染个体的数量。
画图:SIS 模型的 di/dt~i 曲线〔δ > 1〕
在 MATLAB 中,可以使用以下命令画出 SIS 模型的 di/dt~i 曲线〔δ > 1〕:
>> x = 0:0.01:1;
>> y = 0.7 * x - x.^2;
>> plot(x, y);
>> title('SIS 模型的 di/dt~i 曲线 ');
>> xlabel('i');
>> ylabel('di/dt');
画图:SIS 模型的 i~t 曲线〔δ > 1〕
在 MATLAB 中,可以使用以下命令画出 SIS 模型的 i~t 曲线〔δ > 1〕:
>> y = 7 ./ (10 + 340 * exp(-7/10 * t));
>> plot(t, y);
>> title('SIS 模型的 i~t 曲线 ');
>> xlabel('t');
>> ylabel('i');
画图:SIS 模型的 di/dt~i 曲线〔δ ≤ 1〕
在 MATLAB 中,可以使用以下命令画出 SIS 模型的 di/dt~i 曲线〔δ ≤ 1〕:
>> x = 0:0.01:1;
>> y = -0.5 * x.^2 - 0.1 * x;
>> plot(x, y);
>> title('SIS 模型的 di/dt~i 曲线 ');
>> xlabel('i');
>> ylabel('di/dt');
画图:SIS 模型的 i~t 曲线〔δ ≤ 1〕
在 MATLAB 中,可以使用以下命令画出 SIS 模型的 i~t 曲线〔δ ≤ 1〕:
>> y = 1 ./ (-5 + 55 * exp(1/10 * t));
>> plot(t, y);
>> title('SIS 模型的 i~t 曲线 ');
>> xlabel('t');
>> ylabel('i');
SIR 模型是最复杂的传染病模型,它假设感染个体可以传染其他个体,并且一旦感染就不能康复,同时也考虑了康复个体的存在。该模型的数学表达式为:
ds/dt = -a * s * i
di/dt = a * s * i - b * i
dr/dt = b * i
其中,s 是易感个体的数量,i 是感染个体的数量,r 是康复个体的数量,a 是传染率,b 是康复率。
使用 MATLAB 可以求解 SIR 模型的数值解:
function y = ill(t, x)
a = 1;
b = 0.3;
y = [a * x(1) * x(2) - b * x(1), -a * x(1) * x(2)];
[t, x] = ode45('ill', [0:50], [0.02, 0.98]);
可以看到,SI 模型、SIS 模型和 SIR 模型都是数学流行病学的基础,它们描述了传染病在人群中的传播过程。这些模型可以帮助我们更好地理解和预测传染病的传播规律,从而为疾病控制和防疫提供依据。