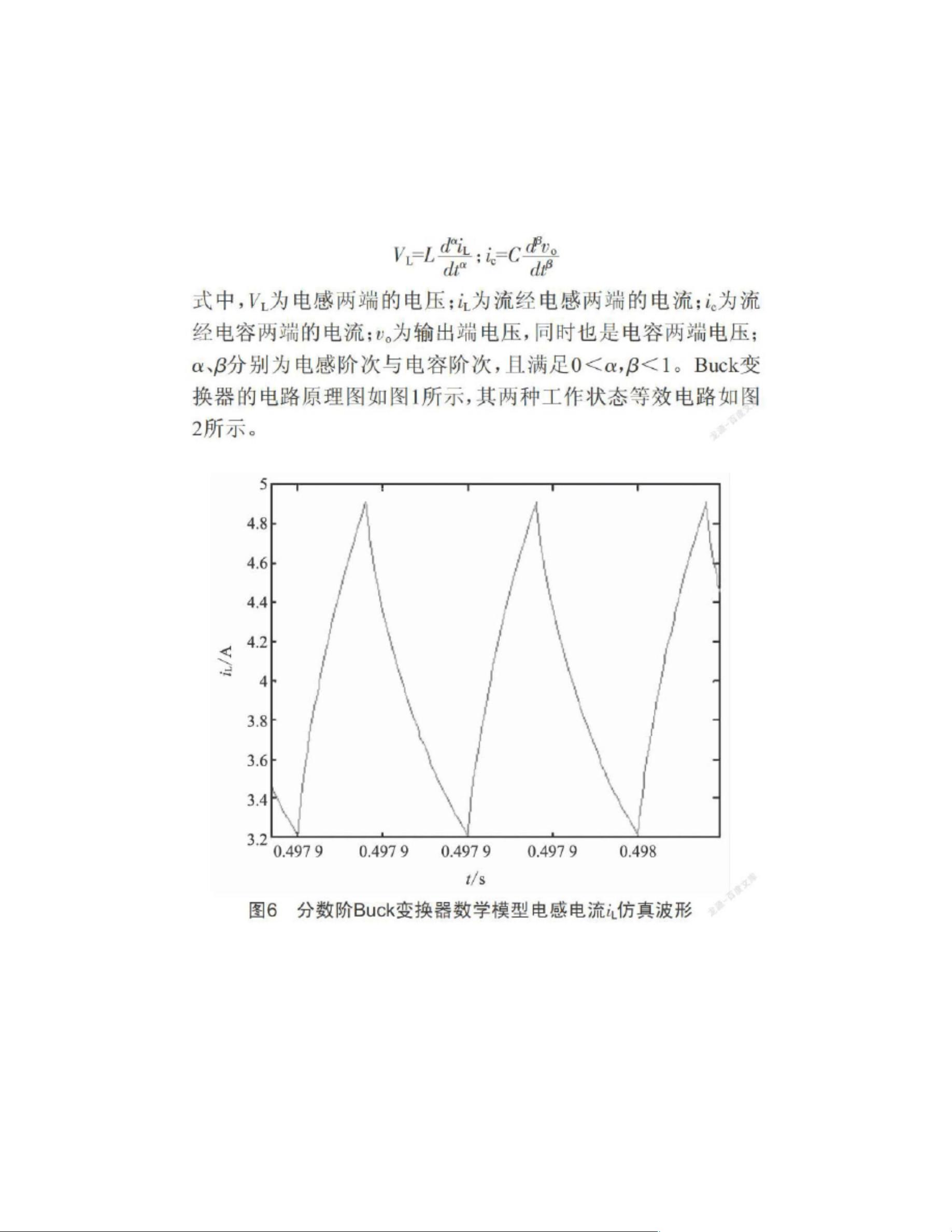
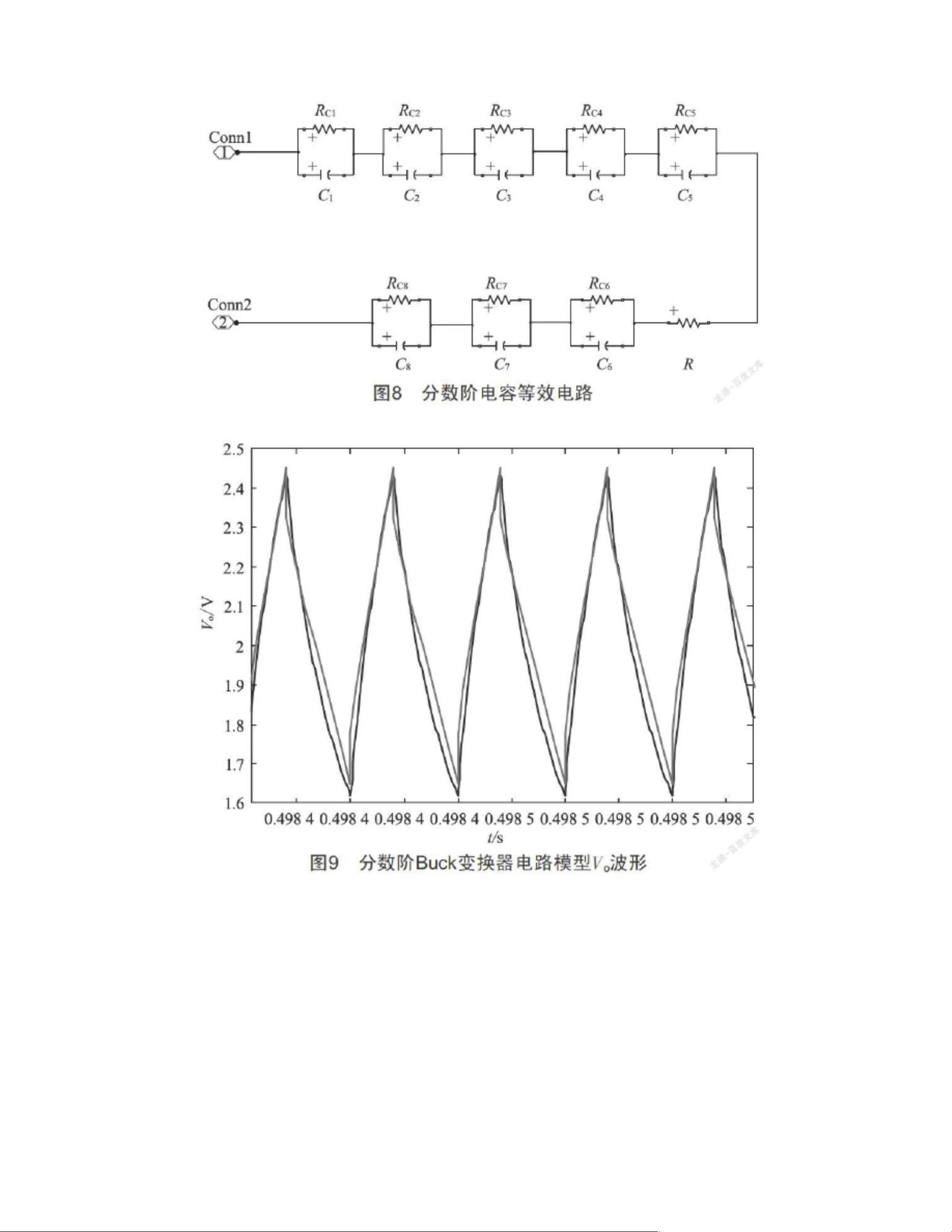
【分数阶微积分理论在Buck电路中的应用】
分数阶微积分理论自1695年由Leibniz提出以来，经过三百多年的发展，逐渐在科学与工程领域中展现出其独特价值。分数阶微积分允许导数和积分的阶次为非整数，这为电路建模提供了更精确的方法，尤其在考虑电感和电容的实际物理特性时，它们的外特性往往呈现出分数阶特性。
【Buck电路的分数阶建模】
Buck电路是一种常见的DC-DC转换器，通过开关控制实现输入电压到输出电压的调节。传统的Buck电路模型通常基于整数阶微积分，但分数阶模型能更准确地模拟电路的实际行为。文献中介绍了利用状态空间平均法建立电感电流连续模式下的分数阶Buck电路模型。通过分析开关S闭合和断开两种状态，结合Caputo分数阶导数，可以推导出占空比至输出电压以及输入电压至输出电压的传递函数。此外，电路的纹波电流也得到了分数阶表达，揭示了纹波电流与电感阶次、输入电压、电感值和开关周期之间的关系。
【分数阶PID控制器】
为了优化电路性能，文献中采用ITAE（Integral of the Absolute Error）最优控制方法设计了分数阶PID控制器。相比于传统的整数阶PID控制器，分数阶PID具有更大的设计自由度，可以调整期望的伯德图形状，以改善系统的稳态响应和动态性能。通过Matlab/Simulink软件进行仿真，验证了分数阶PID控制器的有效性。
【数值仿真验证】
通过Matlab/Simulink建立的分数阶Buck电路仿真模型，结合Oustaloup滤波器的改进算法，进一步确认了分数阶模型的正确性和控制策略的可行性。仿真结果证明了分数阶模型在描述电路行为和控制性能方面的优势。
总结，分数阶微积分理论为Buck电路建模和控制带来了新的视角，它能够更精确地捕捉实际电路的动态特性，提高系统控制的精度和稳定性。随着分数阶理论在电气工程领域的深入研究，未来可能会有更多的电路模型和控制策略受益于这一理论。
