基于贝叶斯决策理论的分类器(1).pptx

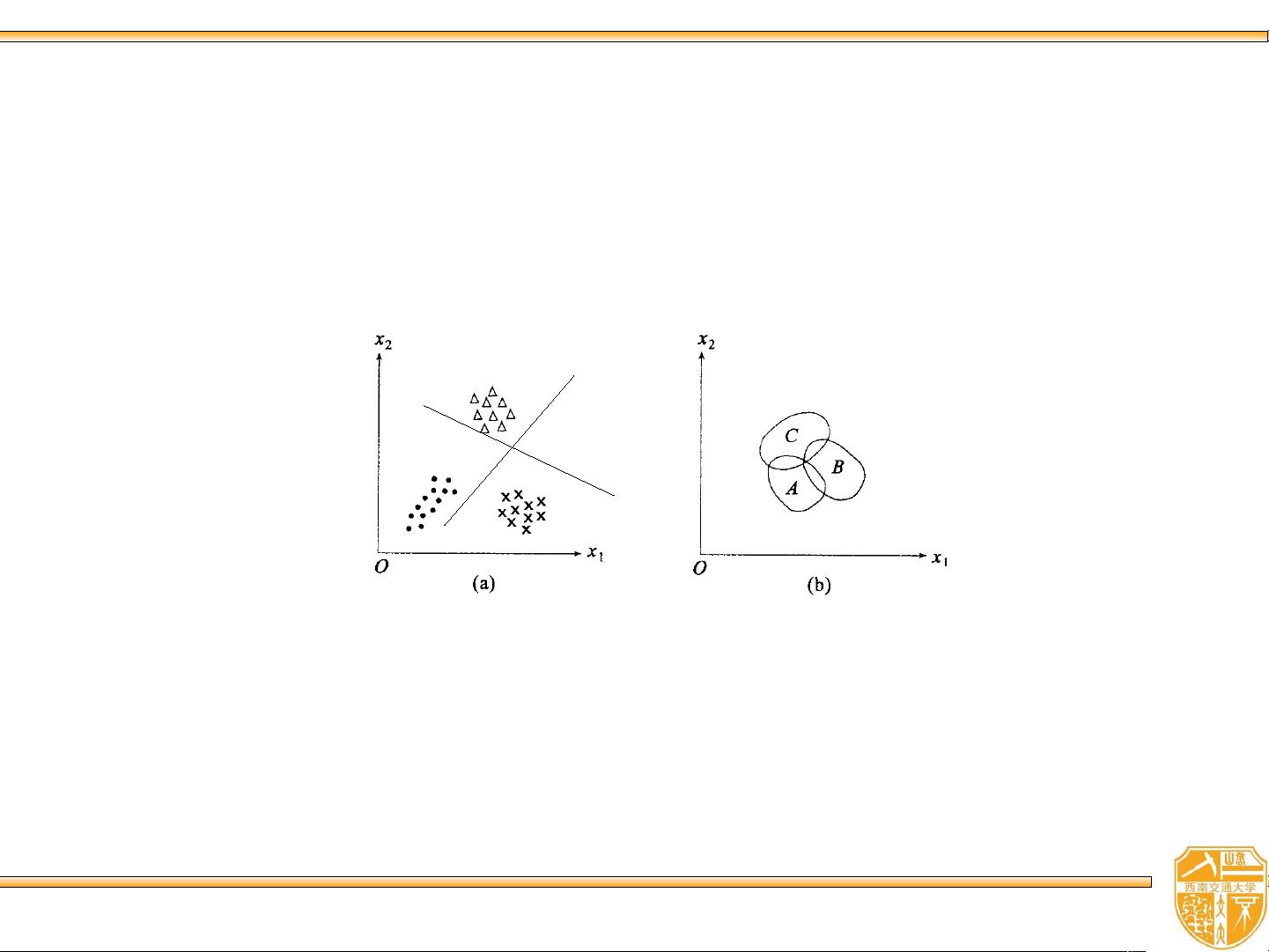
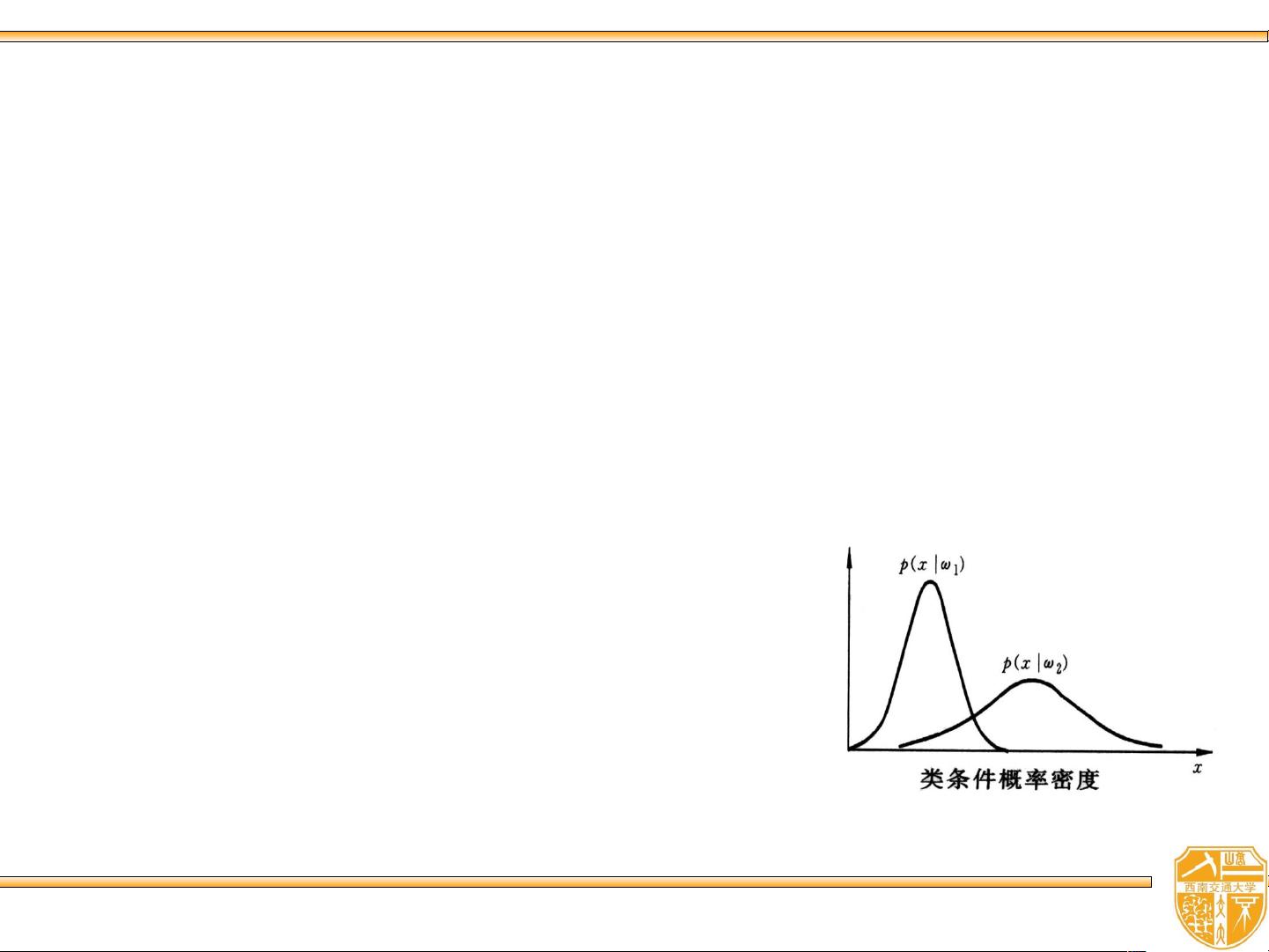
基于贝叶斯决策理论的分类器是一种在模式识别领域广泛应用的方法，它利用概率统计理论来处理分类问题。在这个理论框架下，我们首先需要理解几个关键概念： 1. **模式识别**：模式识别是指通过分析对象的特征值来对其进行分类。特征向量 `x` 由多个特征 `x1, ..., xd` 组成，形成一个 d 维特征空间。每个点 `x` 在这个空间中代表一个模式样本。 2. **贝叶斯决策理论**：该理论是解决不确定性问题的一种统计方法。由于样本的特征值可能存在随机性、特征选择的不完善以及测量误差，导致样本分类具有不确定性。在样本可分性不明显时，就需要利用统计方法，比如最小错误率或最小风险准则来进行决策。 3. **关键概率概念**： - **先验概率** `P(wi)`：表示在没有任何关于样本信息的情况下，类 `wi` 出现的概率。可以通过训练集样本估算。 - **类条件概率密度函数** `p(x|wi)`：表示在给定类 `wi` 的条件下，样本 `x` 出现的概率密度分布。也称为似然函数。 - **后验概率** `P(wi|x)`：表示在给定样本 `x` 的情况下，样本属于类 `wi` 的概率。它是先验概率与类条件概率的结合，通过贝叶斯公式计算得到。 4. **贝叶斯公式**（Bayes' Theorem）：`P(wi|x) = P(x|wi) * P(wi) / P(x)`，其中 `P(x)` 是样本 `x` 的证据因子，通常在分类问题中被看作是归一化常数。 5. **贝叶斯分类规则**：分类时，选择后验概率最大的类作为样本的归属类别，即 `argmax_wi P(wi|x)`。 6. **最小错误率的贝叶斯决策**：在这种策略下，目标是最小化平均错误率。通过设定分类边界，使得误分类的概率达到最小。在一维特征空间中，这通常涉及到找到一个界线，将两类样本分开，使得两边的误分类区域之和最小。 7. **最小风险的贝叶斯决策**：除了错误率，还可以考虑决策的风险。在实际应用中，不同的分类错误可能有不同的后果，因此可以定义一个损失函数来衡量错误的代价。最小风险决策是使总预期损失最小化的决策。 在实际应用贝叶斯决策理论时，通常假设类条件概率密度函数是已知的，或者可以通过训练数据估计。在多类问题中，决策规则可能会更复杂，可能涉及似然比阈值和似然比统计。分类器的性能取决于这些概率估计的准确性和数据的分布特性。 总结来说，基于贝叶斯决策理论的分类器是一种利用概率模型进行分类的方法，它综合了先验知识和样本特征信息，通过计算后验概率来决定样本的类别。这种方法特别适合处理存在不确定性的情况，并且可以根据不同的决策准则（如最小错误率或最小风险）调整分类策略。