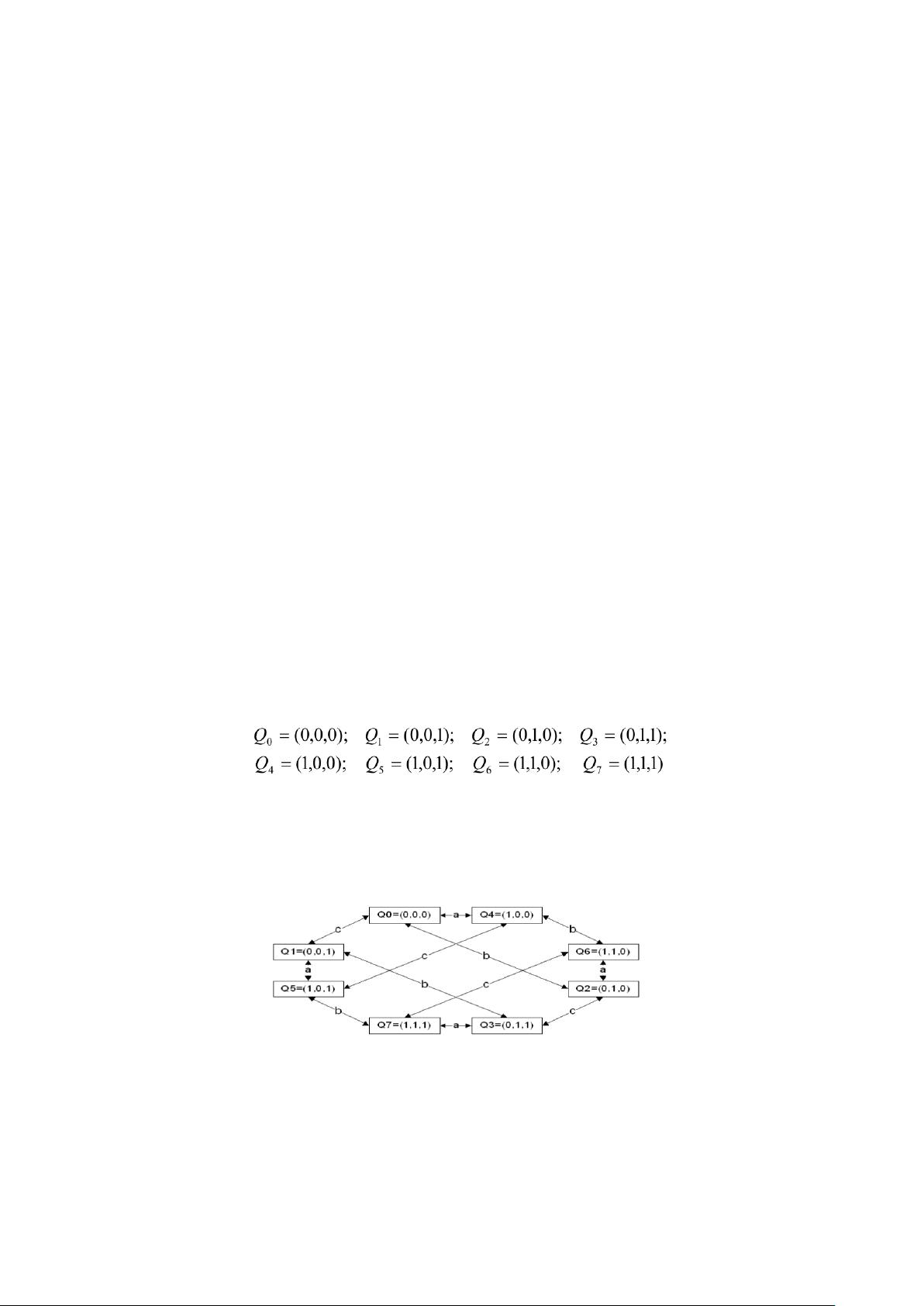
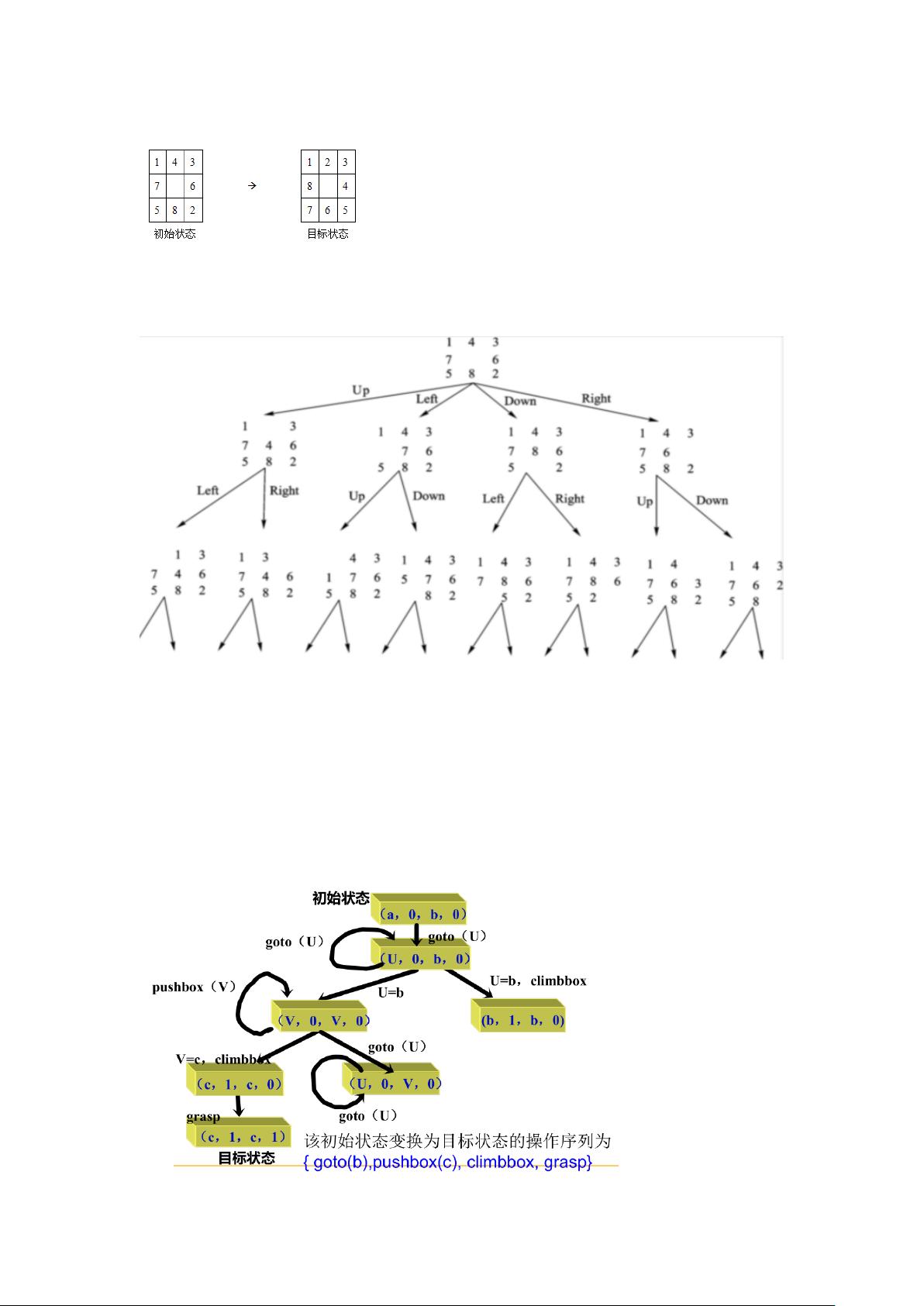
人工智能期末复习资料自用

【人工智能期末复习资料自用】 在人工智能领域，状态空间图是一种重要的问题表示和解决方法，尤其在规划和搜索算法中。状态空间图是由状态和操作算子构成的符号体系，用于表示系统的各种状态以及状态之间的转换关系。在这个图中，节点代表问题的不同状态，而弧则表示状态间的转换，通常携带了对应操作的代价信息。解决问题的过程就是在图中寻找从初始状态到目标状态的最优路径。 状态空间表示法求解问题通常分为四个步骤： 1. 定义问题状态的描述形式，即明确状态的各个组成部分，每个部分代表问题的一个特定方面。 2. 列出所有可能的状态，包括初始状态和目标状态，排除不合理状态。 3. 定义一组操作算子，使问题可以从一个状态转换到另一个状态。 4. 从初始状态开始，通过应用操作算子逐步接近目标状态，直至找到解或证明无解。 例如，钱币翻转问题展示了如何运用状态空间法。有三枚硬币，初始状态为“正”、“反”、“正”，目标是经过三次翻转使所有硬币同一面向上。通过定义状态（三元组Q=（q1，q2，q3），其中1表示“正”，0表示“反”），列举所有可能状态，定义操作（翻转每枚硬币），可以构建状态空间图并找到解。 另一个例子是八数码问题，所有可能的排列组合构成了状态集，通过移动操作（↑, ←, ↓, →）在状态空间图中寻找目标排列。 此外，还有猴子和香蕉问题，用四元序组表示状态（猴子的位置、是否在箱子上、箱子的位置、是否拿到香蕉），并定义猴子的动作（走、推箱子、爬箱子、摘香蕉）来构造状态空间图。 传教士和野人问题中，状态由传教士、野人和船的位置组成，通过定义不同载人数量的船渡河操作（Pij和qij）来构建状态空间图，寻找安全过河的路径。 启发式搜索是一种优化搜索策略，它利用问题的内在特性信息，如启发函数，来指导搜索过程，使搜索更加高效地趋向于目标状态。在搜索过程中，关键在于选择具有最大潜力的节点进行扩展，以期快速找到最优解。这种方法广泛应用于解决复杂问题，如A*搜索算法，它结合了贪婪最佳优先搜索和Dijkstra算法的优点，通过评估节点的启发式价值和实际代价来决定搜索方向。 以上所述的知识点涵盖了人工智能中的基础概念，如状态空间表示、问题求解步骤和启发式搜索策略，这些都是K12教育阶段学习人工智能时的重要内容。通过理解和掌握这些知识点，学生能够更好地理解和解决各种复杂的问题。